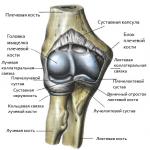
正規分布の定義。 確率変数の正規分布。 STATISTICA 確率計算ツールを使用した正規分布のパーセンテージ ポイントの計算

定義 1

確率変数 $X$ は、その分布密度が次の式で決定される場合、正規分布 (ガウス分布) になります。

\[\varphi \left(x\right)=\frac(1)(\sqrt(2\pi )\sigma )e^(\frac(-((x-a))^2)(2(\sigma )^ 2))\]

ここで、$aϵR$ は数学的期待値、$\sigma >0$ は標準偏差です。

正規分布の密度。

この関数が実際に分布密度であることを示してみましょう。 これを行うには、次の条件を確認してみましょう。

不適切な積分 $\int\limits^(+\infty )_(-\infty )(\frac(1)(\sqrt(2\pi )\sigma )e^(\frac(-((x-a)) ^ 2)(2(\sigma )^2))dx)$。

$\frac(x-a)(\sigma )=t,\ x=\sigma t+a,\ dx=\sigma dt$ と置換してみましょう。

$f\left(t\right)=e^(\frac(-t^2)(2))$ は偶関数なので、次のようになります。

等式が満たされます。つまり、関数 $\varphi \left(x\right)=\frac(1)(\sqrt(2\pi )\sigma )e^(\frac(-((x-a))^2 )(2 (\sigma )^2))$ は確かに、ある確率変数の分布密度です。

正規分布 $\varphi \left(x\right)$ の確率密度関数の簡単な性質をいくつか考えてみましょう。

1. 正規分布の確率密度関数のグラフは直線$x=a$に対して対称になります。
2. 関数 $\varphi \left(x\right)$ は $x=a$ で最大値に達し、 $\varphi \left(a\right)=\frac(1)(\sqrt(2\pi )\sigma ) e^(\frac(-((a-a))^2)(2(\sigma )^2))=\frac(1)(\sqrt(2\pi )\sigma )$
3. 関数 $\varphi \left(x\right)$ は、$x>a$ になるほど減少し、$x になるほど増加します。
4. 関数 $\varphi \left(x\right)$ には $x=a+\sigma $ と $x=a-\sigma $ に変曲点があります。
5. 関数 $\varphi \left(x\right)$ は、 $x\to \pm \infty $ として $Ox$ 軸に漸近します。
6. 概略グラフは次のようになります (図 1)。

図1. 1. 正規分布密度グラフ

$a=0$ の場合、関数のグラフは $Oy$ 軸に関して対称であることに注意してください。 したがって、関数 $\varphi \left(x\right)$ は偶数です。

正規確率分布関数。

正規分布の確率分布関数を求めるには、次の式を使用します。

したがって、

定義 2

$a=0,\ \sigma =1$ の場合、関数 $F(x)$ は標準正規分布と呼ばれます。つまり、次のとおりです。

ここで $Ф\left(x\right)=\frac(1)(\sqrt(2\pi ))\int\limits^x_0(e^(\frac(-t^2)(2))dt)$ - ラプラス関数。

定義 3

関数 $Ф\left(x\right)=\frac(1)(\sqrt(2\pi ))\int\limits^x_0(e^(\frac(-t^2)(2))dt)$確率積分といいます。

正規分布の数値的特徴。

数学的期待値: $M\left(X\right)=a$。

分散: $D\left(X\right)=(\sigma )^2$。

平均二乗分布: $\sigma \left(X\right)=\sigma $。

例1

正規分布の概念に関する問題を解く例。

問題 1: パス長 $X$ はランダムな連続変数です。 $X$ は正規分布法則に従って分布し、その平均値は $4$ キロメートルに等しく、標準偏差は $100$ メートルに等しくなります。

1. 分布密度関数 $X$ を求めます。
2. 分布密度の模式的なグラフを描きます。
3. 確率変数 $X$ の分布関数を求めます。
4. 分散を求めます。

1. まず、すべての量を 1 次元で想像してみましょう: 100m=0.1km

定義 1 から、次のことが得られます。

\[\varphi \left(x\right)=\frac(1)(0.1\sqrt(2\pi ))e^(\frac(-((x-4))^2)(0.02 ))\]

($a=4\ kmなので、\ \sigma =0.1\ km)$

1. 分布密度関数の性質を利用すると、関数 $\varphi \left(x\right)$ のグラフは直線 $x=4$ に関して対称であることがわかります。

関数は $\left(a,\frac(1)(\sqrt(2\pi )\sigma )\right)=(4,\ \frac(1)(0,1\sqrt( 2\pi )))$

概略グラフは次のようになります。

図2.

1. 分布関数の定義により $F\left(x\right)=\frac(1)(\sqrt(2\pi )\sigma )\int\limits^x_(-\infty )(e^(\frac( -( (t-a))^2)(2(\sigma )^2))dt)$、次のようになります。

1. $D\left(X\right)=(\sigma )^2=0.01$。

(実際の、厳密に肯定的な)

正規分布、 とも呼ばれている ガウス分布または ガウス - ラプラス- 確率分布。1 次元の場合、ガウス関数と一致する確率密度関数によって指定されます。

ここで、パラメータ μ は分布の期待値 (平均値)、中央値、および最頻値であり、パラメータ σ は分布の標準偏差 (σ² は分散) です。

したがって、1 次元正規分布は 2 パラメータ群の分布です。 多変量の場合については、「多変量正規分布」の記事で説明されています。

標準正規分布は、数学的期待値 μ = 0 および標準偏差 σ = 1 を持つ正規分布と呼ばれます。

百科事典 YouTube

• 1 / 5

  科学の多くの分野 (数学統計や統計物理学など) における正規分布の重要性は、確率論の中心極限定理に基づいています。 観測の結果が、相互依存性の弱い多数のランダムな量の合計であり、それぞれの量が合計に対してわずかに寄与する場合、項の数が増加するにつれて、中心化され正規化された結果の分布は正規になる傾向があります。 この確率論の法則により、正規分布が広範囲に分布することになり、これがその名前の理由の 1 つになりました。

  プロパティ

  瞬間

  確率変数の場合 X 1 (\displaystyle X_(1))そして X 2 (\displaystyle X_(2))独立しており、数学的期待を伴う正規分布を持っています μ 1 (\displaystyle \mu _(1))そして μ 2 (\displaystyle \mu _(2))と差異 σ 1 2 (\displaystyle \sigma _(1)^(2))そして σ 2 2 (\displaystyle \sigma _(2)^(2))したがって、 X 1 + X 2 (\displaystyle X_(1)+X_(2))数学的期待を伴う正規分布もあります μ 1 + μ 2 (\displaystyle \mu _(1)+\mu _(2))と分散 σ 1 2 + σ 2 2 。 (\displaystyle \sigma _(1)^(2)+\sigma _(2)^(2)。)したがって、正規確率変数は、任意の数の独立した正規確率変数の合計として表すことができるということになります。

  最大エントロピー

  正規分布は、分散が所定の値を超えないすべての連続分布の中で最大の差分エントロピーを持ちます。

  通常の擬似乱数変数のモデル化

  最も単純な近似モデリング方法は、中心極限定理に基づいています。 つまり、有限分散を持つ複数の独立した同一分布量を加算すると、その合計は分布します。 約大丈夫。 例えば、独立したものを標準で100個追加した場合 均等に分散確率変数の場合、合計の分布はおよそ次のようになります。 普通.

  正規分布の擬似乱数変数をプログラムで生成するには、Box-Muller 変換を使用することをお勧めします。 これにより、1 つの均一分布値に基づいて 1 つの正規分布値を生成できます。

  性質と応用における正規分布

  正規分布は自然界でよく見られます。 たとえば、次の確率変数は正規分布によって適切にモデル化されています。

  • 撮影時のズレ。
  • 測定誤差（ただし、測定器によっては誤差が正規分布にならない場合があります）。
  • 集団内の生物のいくつかの特徴。

  この分布は分散が有限で無限に割り切れる連続分布であるため、非常に広く普及しています。 したがって、二項やポアソンなど、他のいくつかの手法では極限内でこれにアプローチします。 この分布は、多くの非決定的な物理プロセスをモデル化します。

  他のディストリビューションとの関係

  • 正規分布はピアソン XI 型分布です。
  • 独立した標準正規分布確率変数のペアの比率は、コーシー分布を持ちます。 つまり、確率変数が X (\表示スタイル X)関係を表します X = Y / Z (\displaystyle X=Y/Z)（どこ Y (\表示スタイル Y)そして Z (\displaystyle Z)- 独立した標準正規確率変数) の場合、コーシー分布になります。
  • もし z 1 , … , z k (\displaystyle z_(1),\ldots ,z_(k))- 共に独立した標準正規確率変数、つまり z i 〜 N (0 , 1) (\displaystyle z_(i)\sim N\left(0,1\right))、次に確率変数 x = z 1 2 + … + z k 2 (\displaystyle x=z_(1)^(2)+\ldots +z_(k)^(2))は、k 自由度のカイ二乗分布を持ちます。
  • 確率変数の場合 X (\表示スタイル X)が対数正規分布の対象となる場合、その自然対数は正規分布になります。 つまり、もし X 〜 Log N (μ , σ 2) (\displaystyle X\sim \mathrm (LogN) \left(\mu ,\sigma ^(2)\right))、 それ Y = ln ⁡ (X) 〜 N (μ , σ 2) (\displaystyle Y=\ln \left(X\right)\sim \mathrm (N) \left(\mu ,\sigma ^(2)\right ))。 そしてその逆の場合は、 Y 〜 N (μ , σ 2) (\displaystyle Y\sim \mathrm (N) \left(\mu ,\sigma ^(2)\right))、 それ X = exp ⁡ (Y) ∼ Log N (μ , σ 2) (\displaystyle X=\exp \left(Y\right)\sim \mathrm (LogN) \left(\mu ,\sigma ^(2) \右））.
  • 2 つの標準正規確率変数の二乗の比は次のようになります。

  連続確率変数の正規確率分布の法則は、多くの実際的な研究の基礎となるため、さまざまな理論法則の中でも特別な位置を占めています。 生産プロセスに関連するほとんどのランダム現象を説明します。

  正規分布則に従うランダム現象には、生産パラメータの測定誤差、技術的な製造誤差の分布、ほとんどの生物体の身長と重量などが含まれます。

  普通 連続確率変数の確率分布の法則であり、微分関数で記述されます。

  a - 確率変数の数学的期待値。

  正規分布の標準偏差。

  正規分布の微分関数をグラフ化したものを正規曲線（ガウス曲線）といいます（図7）。

  

  米。 7 ガウス曲線

  法線曲線 (ガウス曲線) のプロパティ:

  1. 曲線は直線 x = a に関して対称です。

  2. 正規曲線は X 軸の上にあります。つまり、X のすべての値に対して、関数 f(x) は常に正です。

  3. ox 軸はグラフの水平漸近線です。

  4. x = a の場合、関数 f(x) の最大値は次のとおりです。

  ,

  点 A と点 B では、曲線には縦座標が等しい変曲点があります。

  

  同時に、正規分布確率変数の数学的期待値からの偏差の絶対値が標準偏差を超えない確率は 0.6826 に等しくなります。

  点 E と G では、 と について、関数 f(x) の値は次と等しくなります。

  

  また、正規分布確率変数の数学的期待値からの偏差の絶対値が標準偏差の 2 倍を超えない確率は 0.9544 です。

  x 軸に漸近すると、点 C と D、および のガウス曲線は x 軸に非常に近くなります。 これらの点では、関数 f(x) の値は非常に小さくなります。

  

  また、正規分布確率変数の数学的期待値からの偏差の絶対値が標準偏差の 3 倍を超えない確率は 0.9973 です。 ガウス曲線のこの性質は「」と呼ばれます。 スリーシグマの法則".

  
  
  

  確率変数が正規分布している場合、数学的期待値からの偏差の絶対値は標準偏差の 3 倍を超えません。

  パラメーター a (確率変数の数学的期待値) の値を変更しても、正規曲線の形状は変わりません。ただ、X 軸に沿った変位が生じるだけです。つまり、a が増加すると右に、a が増加すると左に変位します。減少します。

  a=0 の場合、正規曲線は縦軸に対して対称になります。

  パラメータの値 (標準偏差) を変更すると、法線曲線の形状が変化します。法線曲線の縦軸が増加すると、縦軸が減少し、曲線は X 軸に沿って伸び、X 軸に押し付けられます。 減少すると、通常の曲線の縦軸が増加し、曲線は X 軸に沿って縮小し、より「尖った」ものになります。

  同時に、どのような値についても、正規曲線と X 軸で囲まれた面積は 1 に等しいままです (つまり、正規分布確率変数が正規曲線の X 軸で囲まれた値を取る確率)は1に等しい)。

  任意のパラメータと をもつ正規分布、すなわち微分関数で記述される

  

  呼ばれた 一般的な正規分布.

  パラメーター付きの正規分布は次のように呼ばれます。 正規化された分布(図8)。 正規化された分布では、微分分布関数は次と等しくなります。

  

  米。 8 正規化された曲線

  一般正規分布の累積関数は次の形式になります。

  確率変数 X が区間 (c, d) 内で正規法則に従って分布するとします。 この場合、X が区間 (c, d) に属する値を取る確率は次のようになります。

  

  例。確率変数 X は正規法則に従って分布します。 この確率変数の数学的期待値と標準偏差は、a=30 および に等しくなります。 X が区間 (10, 50) 内の値を取る確率を求めます。

  条件別: 。 それから

  既製のラプラス テーブル (付録 3 を参照) を使用します。

  正規分布の法則は、実際に最もよく遭遇します。 この法則を他の法則と区別する主な特徴は、これが制限的な法則であり、非常に一般的な典型的な条件下では他の分配法則がそれに近づくことです。

  意味。 連続確率変数 X は 通常の法律分布(ガウスの法則 )パラメータ a と σ 2 を使用して、その確率密度が f の場合(バツ) のように見える:

  .

  (6.19)

  正規分布曲線は次のように呼ばれます 普通または ガウス曲線。 図では、 6.5 a)、b) はパラメータ付きの正規曲線を示します あそして σ 2と分布関数グラフ。

  正規曲線が直線に対して対称であることに注目してみましょう。 バツ = あ、点で最大値があります バツ = あ、 に等しい、および 2 つの変曲点 バツ = あ σ 縦座標付き。

  正規法則密度表現では、分布パラメータが文字で示されていることに注意してください。 あそして σ 2、数学的な期待値と分散を表すために使用しました。 この偶然は偶然ではありません。 正規法則のパラメータの確率的理論的意味を確立する定理を考えてみましょう。

  定理。 正規法則に従って分布する確率変数 X の数学的期待値は、この分布のパラメータ a に等しい、つまり

  M(バツ) = あ,

  (6.20)

  とその分散 - パラメータ σ 2 へ、つまり

  D(バツ) = σ 2.

  (6.21)

  パラメーターを変更すると法線カーブがどのように変化するかを調べてみましょう あそして σ .

  もし σ = const、パラメータが変更されます ある (あ 1 < あ 2 < あ 3)、つまり 分布の対称中心に位置すると、正規曲線は形状を変えることなく横軸に沿って移動します (図 6.6)。

  

  米。 6.6

  

  米。 6.7

  もし あ= const とパラメータの変更 σ 、その後、曲線の最大値の縦軸が変化します f 最大値(ある) = 。 増やす場合 σ 最大値の縦座標は減少しますが、分布曲線の下の面積は 1 に等しいままでなければならないため、曲線はより平坦になり、x 軸に沿って伸びます。 減少時 σ 逆に、通常の曲線は上に伸びると同時に横から圧縮されます (図 6.7)。

  したがって、パラメータは ある位置とパラメータを特徴付ける σ – 通常の曲線の形状。

  パラメータ付き確率変数の正規分布則 ある= 0 および σ = 1 が呼び出されます 標準または 正規化された、対応する正規曲線は次のようになります。 標準または 正規化された.

  正規分布関数に従って分布する確率変数の分布関数を直接求めることが難しいのは、正規分布関数の積分が初等関数では表現できないためです。 ただし、式 or の定積分を表す特別な関数を通じて計算できます。 この関数は呼び出されます ラプラス関数、表がそれ用にまとめられています。 この関数にはさまざまな種類があります。たとえば、次のとおりです。

  , .

  関数を使っていきます

  正規法則に従って分布する確率変数の性質を考えてみましょう。

  1. 正規法則に従って分布する確率変数 X が区間に入る確率 [α , β ] に等しい

  この式を使用して、さまざまな値の確率を計算します。 δ (ラプラス関数値の表を使用):

  で δ = σ = 2Ф(1) = 0.6827;

  で δ = 2σ = 2Ф(2) = 0.9545;

  で δ = 3σ = 2Ф(3) = 0.9973。

  これはいわゆる「」につながります。 スリーシグマの法則»:

  確率変数 X がパラメーター a と σ を持つ正規分布則を持っている場合、その値が区間内にあることはほぼ確実です。(ある – 3σ ; ある + 3σ ).

  例6.3。ある年齢層の男性の身長が正規分布する確率変数であると仮定する バツパラメータ付き あ= 173 と σ 2 = 36、次を求めます。

  1. 確率変数の確率密度と分布関数の表現 バツ;

  2. 第 4 の身長（176 ～ 183 cm）のスーツのシェアと第 3 の身長（170 ～ 176 cm）のスーツのシェア。これらは、この年齢層の総生産量に含める必要があります。

  3. 確率変数の「スリー シグマ ルール」を定式化する バツ.

  1. 確率密度を求める

  

  と確率変数 X の分布関数

  = .

  2. 身長 4 (176 – 182 cm) のスーツの割合を確率として求めます。

  R(176 ≤ バツ ≤ 182) = = Ф(1.5) – Ф(0.5)。

  ラプラス関数の値の表によると（ 付録 2） 我々は気づく：

  F(1.5) = 0.4332、F(0.5) = 0.1915。

  ようやく得られる

  R(176 ≤ バツ ≤ 182) = 0,4332 – 0,1915 = 0,2417.

  3番目の身長（170～176cm）のスーツのシェアも同様の方法で求めることができます。 ただし、この間隔が数学的期待に対して対称であることを考慮すると、これを行うのが簡単になります。 あ= 173、つまり 不等式 170 ≤ バツ≤ 176 は不等式に相当します │ バツ– 173│≤ 3. それでは

  R(170 ≤バツ ≤176) = R(│バツ– 173│≤ 3) = 2Ф(3/6) = 2Ф(0.5) = 2・0.1915 = 0.3830。

  3. 確率変数 X の「スリー シグマ ルール」を定式化してみましょう。

  この年齢層の男性の身長の範囲はほぼ確実です。 あ – 3σ = 173 – 3 6 = 155 ～ あ + 3σ = 173 + 3・6 = 191、つまり 155 ≤ バツ ≤ 191. ◄

  
  

  7. 確率論の極限定理

  確率変数を研究するときにすでに述べたように、1 回のテストの結果として確率変数がどのような値を取るかを事前に予測することは不可能です。考慮できない多くの理由によって決まります。

  しかし、テストを何度も繰り返すと、確率変数の合計の挙動はランダム性をほとんど失い、自然になります。 パターンの存在は、全体として、明確に定義された法則の対象となる確率変数を生成する現象の質量的性質と正確に関連付けられています。 質量現象の安定性の本質は次のとおりです。個々のランダム現象の特定の特徴は、そのような現象の質量の平均結果にはほとんど影響を与えません。 個々の現象では避けられない、平均からのランダムな偏差が、全体としては相互に打ち消し合い、平準化され、平準化されます。

  この平均値の安定性は、広い意味で理解される「大数の法則」の物理的内容を表します。つまり、非常に多数のランダム現象の場合、その結果は事実上ランダムではなくなり、次のように予測できます。高い確実性。

  狭い意味での確率論における「大数の法則」は、一連の数学定理として理解され、それぞれの定理は、特定の条件下で、多数の実験の平均特性が一定の値に近づくという事実を確立します。特定の定数。

  大数の法則は、確率論の実際の応用において重要な役割を果たします。 確率変数は、特定の条件下では非ランダム変数とほぼ同じように動作するという特性により、自信を持ってこれらの量を操作し、大量のランダム現象の結果をほぼ完全な確実性で予測することができます。

  大量ランダム現象の分野におけるそのような予測の可能性は、確率変数の制限値ではなく、分布の制限法則に関係する別のグループの極限定理の存在によってさらに拡張されます。 ここでは「中心極限定理」として知られる一連の定理について話します。 中心極限定理のさまざまな形式は、確率変数の和のこの制限特性が確立される条件が互いに異なります。

  さまざまな形式の大数の法則とさまざまな形式の中心極限定理は、いわゆる一連の集合を形成します。 極限定理確率論。 極限定理を使用すると、ランダム現象の分野で科学的な予測を行うことができるだけでなく、その予測の精度を評価することもできます。

  意味。 普通連続確率変数の確率分布であり、確率密度によって記述されます。

  正規分布則とも呼ばれます ガウスの法則.

  正規分布の法則は確率論の中心的な位置を占めます。 これは、確率変数が多数の異なる要因の作用の結果であるすべての場合に、この法則が現れるという事実によるものです。 他のすべての分配法則は正規法則に近づきます。

  分布密度に含まれるパラメータと がそれぞれ、確率変数 X の数学的期待値と標準偏差であることは簡単に示されます。

  分布関数を求めてみましょう F(x).

  

  正規分布の密度グラフは次のように呼ばれます。 通常の曲線または ガウス曲線.

  法線曲線には次の特性があります。

  1) 関数は数直線全体で定義されます。

  ２）みんなの前で バツ分布関数は正の値のみを取ります。

  3) OX 軸は確率密度グラフの水平漸近線です。 引数の絶対値を無制限に増加させる バツ、関数の値はゼロになる傾向があります。

  4) 関数の極値を見つけます。

  

  なぜなら で y' > 0で バツ< m そして やあ< 0 で x > メートル、そしてその時点で x = t関数の最大値は です。

  5) 関数は直線に対して対称である x = a、 なぜなら 違い

  (× – a) は二乗分布密度関数に含まれます。

  6) グラフの変曲点を見つけるために、密度関数の 2 次導関数を求めます。

  

  で x = メートル+と x = メートル- s 二次導関数はゼロに等しく、これらの点を通過すると符号が変わります。 これらの点で、関数には変曲点があります。

  これらの点での関数の値は です。

  分布密度関数をプロットしてみましょう。

  

  グラフは次のために作成されました T=0 と、標準偏差の 3 つの値 (s = 1、s = 2、s = 7) が考えられます。ご覧のとおり、標準偏差の値が増加するにつれて、グラフは平坦になり、最大値は減少します。

  もし あ> 0 の場合、グラフは正の方向にシフトします。 あ < 0 – в отрицательном.

  で あ= 0 および s = 1 の曲線が呼び出されます。 正規化された。 正規化された曲線方程式:

  簡潔にするために、彼らは、CB X は法則 N(m, s) に従うと言います。 X ~ N(m, s)。 パラメーター m と s は、分布の主な特性 (m = m X、s = s X =) と一致します。 CB X ~ N(0, 1) の場合、それが呼び出されます。 標準化された正常値。 DF標準化正常値と呼ばれる ラプラス関数と表されます Ф(x)。 これを使用すると、正規分布 N(m, s) の区間確率を計算できます。

  P(x 1 £ X< x 2) = Ф - Ф .

  正規分布の問題を解くときは、多くの場合、ラプラス関数の表の値を使用する必要があります。 ラプラス関数では次の関係が成り立つので、 F(-x) = 1 - F(x)であれば、関数のテーブル値があれば十分です F(x)正の引数値の場合のみ。

  数学的期待に関して対称な区間に入る確率については、次の式が有効です。 P(|X - m X |< e) = 2×Ф(e/s) - 1.

  正規分布の中心モーメントは漸化式 m n +2 = (n+1)s 2 m n , n = 1, 2, ... を満たします。 したがって、奇数次のすべての中心モーメントはゼロに等しいということになります (m 1 = 0 であるため)。

  正規法則に従って分布した確率変数が指定された区間に収まる確率を求めてみましょう。

  

  と表しましょう

  なぜなら 積分が初等関数で表現されていない場合、その関数が考慮されます。

  ,

  と呼ばれるもの ラプラス関数または 確率積分.

  さまざまな値に対するこの関数の値 バツ計算され、特別な表に表示されます。

  以下はラプラス関数のグラフです。

  

  ラプラス関数には次の特性があります。

  2) ふ(- バツ) = -Ф( バツ);

  ラプラス関数とも呼ばれます 誤差関数と erf を示します バツ.

  まだ使用中 正規化されたラプラス関数。次の関係によりラプラス関数に関連付けられます。

  

  以下は正規化されたラプラス関数のグラフです。

  

  正規分布則を考慮するとき、として知られる重要な特殊なケースが際立ちます。 スリーシグマの法則.

  正規分布確率変数の数学的期待値からの偏差が所定の値 D 未満である確率を書き留めてみましょう。

  D = 3s とすると、ラプラス関数の値のテーブルを使用して次の値が得られます。

  それらの。 確率変数が標準偏差の 3 倍を超えて数学的期待から逸脱する確率は、実質的にゼロです。

  このルールはと呼ばれます スリーシグマの法則.

  実際には、任意の確率変数に対して 3 シグマ規則が満たされる場合、この確率変数は正規分布を持つと考えられています。

  例。列車は100両編成です。 各車の質量は、数学的期待を伴う正規法則に従って分布する確率変数です。 あ= 65 t、標準偏差 s = 0.9 t この機関車は 6600 t 以下の重さの列車を運ぶことができますが、そうでない場合は 2 台目の機関車を連結する必要があります。 2 番目の機関車が必要なくなる確率を求めます。

  列車の質量の予想質量からの偏差 (100 × 65 = 6500) が 6600 – 6500 = 100 トンを超えない場合、2 台目の機関車は必要ありません。

  なぜなら 各車両の質量は正規分布するので、列車全体の質量も正規分布することになります。

  我々が得る：

  例。正規分布確率変数 X は、そのパラメータによって指定されます – a =2 –数学的期待値と s = 1 – 標準偏差。 確率密度を書いてプロットし、X が区間 (1; 3) の値を取る確率を求め、X が数学的期待値から (絶対値で) 2 以下だけ逸脱する確率を求める必要があります。 。

  分布密度は次の形式になります。

  

  グラフを作成しましょう:

  

  確率変数が区間 (1; 3) に該当する確率を求めてみましょう。

  確率変数が数学的期待値から 2 以下で逸脱する確率を求めてみましょう。

  正規化ラプラス関数を使用しても同じ結果が得られます。

  講義 8 大数の法則（第2節）

  講義概要

  中心極限定理 (独立した同一分布の確率変数の一般的な定式化と特定の定式化)。

  チェビシェフの不等式。

  チェビシェフ形式の大数の法則。

  イベント頻度の概念。

  確率の統計的理解。

  ベルヌーイ形式の大数の法則。

  統計パターンの研究により、特定の条件下では、多数の確率変数の全体的な挙動がそのランダムな性質をほぼ失い、自然になる (言い換えれば、ある平均的な挙動からのランダムな偏差が互いに打ち消し合う) ことが証明されるようになりました。 ）。 特に、個々の項の合計に対する影響が一様に小さい場合、合計の分布法則は正規に近づきます。 このステートメントの数学的定式化は、と呼ばれる定理のグループで与えられます。 大数の法則.

  大数の法則- ある非常に一般的な条件下で、ランダムな要因の共同作用によって、偶然とはほとんど関係のない結果がもたらされる一般原則。 この原則の最初の例は、試行回数が増加するにつれて、ランダムなイベントの発生頻度とその確率が収束することです (実際には、たとえば、ある回答者の何らかの性質の発生頻度を使用する場合などによく使用されます)対応する確率のサンプル推定値としてのサンプル）。

  エッセンス 大数の法則それは、多数の独立した実験を行うと、ある事象の発生頻度がその確率に近づくということです。

  中心極限定理 (CLT) (同一分布の SV に対する Lyapunov A.M. の定式化)。ペアごとに独立した SV X 1 、X 2 、...、X n 、... が有限の数値特性 M = m および D = s 2 を持つ同じ分布則を持つ場合、n ® ¥ について SV の分布則は無限に近づきます。正規法則 N(n×m, )。

  結果。 SV 定理の条件にある場合 の場合、n ® ¥ として、SV Y の分布法則は正規法則 N(m, s/ ) に無限に近づきます。

  ド・モアブル・ラプラスの定理。 SV K を、ベルヌーイ スキームに従った n 回の試行における「成功」の数とする。 次に、n ® ¥ と 1 回の試行における「成功」の確率の固定値 p を使用すると、SV K の分布則は正規則 N(n×p, ) に無限に近づきます。

  結果。定理の条件において、SV K の代わりに SV K/n (ベルヌーイ スキームによる n 回の試行における「成功」の頻度) を考慮すると、n ® ¥ と p の固定値の分布法則が無期限に計算されます。は正規法則 N(p, ) に近づきます。

  コメント。 SV K を、ベルヌーイ スキームに従った n 回の試行における「成功」の数とする。 このような SV の分布法則は二項法則です。 次に、 n ® ¥ に対して、二項法則には 2 つの極限分布があります。

  n分布 ポワソン(n ® ¥ および l = n×p = const の場合);

  n分布 ガウス N(n×p, ) (n ® ¥ および p = const の場合)。

  例。 1 回の試行で「成功」する確率は、わずか p = 0.8 です。 少なくとも 0.9 の確率で、ベルヌーイ スキームに従ったテストで観察された「成功」の頻度が確率 p から e = 0.01 以下で逸脱すると期待できるようにするには、テストを何回実行する必要がありますか?

  解決。比較のために、2 つの方法で問題を解決してみましょう。

  フェイスブック

  ツイッター

  連絡中

  クラスメイト

  Google+