Saīsināti kubu reizināšanas piemēri. Saīsinātās reizināšanas formulas. Detalizēta teorija ar piemēriem. Polinoma reizināšana ar polinomu

Aprēķinot algebriskos polinomus, lai vienkāršotu aprēķinus, mēs izmantojam saīsinātās reizināšanas formulas. Kopumā ir septiņas šādas formulas. Viņi visi ir jāzina no galvas.

Tāpat jāatceras, ka formulās "a" un "b" vietā var būt gan skaitļi, gan jebkuri citi algebriski polinomi.

Kvadrātu atšķirība

Atcerieties!

Kvadrātu atšķirība divi skaitļi ir vienādi ar šo skaitļu un to summas starpības reizinājumu.

a 2 − b 2 = (a − b)(a + b)

• 15 2–2 2 = (15–2) (15 + 2) = 13 17 = 221
• 9a 2 - 4b 2 ar 2 = (3a - 2bc) (3a + 2bc)

summas kvadrāts

Atcerieties!

Divu skaitļu summas kvadrāts ir vienāds ar pirmā skaitļa kvadrātu plus divreiz pirmā skaitļa reizinājumu un otro plus otrā skaitļa kvadrātu.

(a + b) 2 = a 2 + 2ab + b 2

Ņemiet vērā, ka ar šo samazināto reizināšanas formulu to ir viegli izdarīt atrodiet lielu skaitļu kvadrātus neizmantojot kalkulatoru vai garo reizināšanu. Paskaidrosim ar piemēru:

Atrodiet 112 2 .

• Sadalīsim 112 skaitļu summā, kuru kvadrātus mēs labi atceramies.
  112 = 100 + 1
• Iekavās ierakstām skaitļu summu un pāri iekavām liekam kvadrātu.
  112 2 = (100 + 12) 2
• Izmantosim summas kvadrāta formulu:
  112 2 = (100 + 12) 2 = 100 2 + 2 100 12 + 12 2 = 10 000 + 2 400 + 144 = 12 544

Atcerieties, ka kvadrātsummas formula ir derīga arī visiem algebriskajiem polinomiem.

• (8a + c) 2 = 64a 2 + 16ac + c 2

Brīdinājums!

(a + b) 2 nav vienāds ar (a 2 + b 2)

Atšķirības kvadrāts

Atcerieties!

Divu skaitļu starpības kvadrāts ir vienāds ar pirmā skaitļa kvadrātu mīnus divreiz pirmā un otrā reizinājums plus otrā skaitļa kvadrāts.

(a − b) 2 = a 2 − 2ab + b 2

Ir arī vērts atcerēties ļoti noderīgu transformāciju:

(a–b) 2 = (b–a) 2

Iepriekš minēto formulu pierāda, vienkārši paplašinot iekavas:

(a - b) 2 = a 2 -2ab + b 2 = b 2 - 2ab + a 2 = (b - a) 2

summas kubs

Atcerieties!

Divu skaitļu summas kubs ir vienāds ar pirmā skaitļa kubu, kuram pieskaitīts trīs reizes pirmā skaitļa kvadrāts, kas reizināts ar otro plus trīs reizes reizinājums ar pirmo skaitļa kvadrātu un otrā kubu.

(a + b) 3 = a 3 + 3a 2 b + 3ab 2 + b 3

Kā atcerēties summas kubu

Atcerēties šo "briesmīgā" izskata formulu ir pavisam vienkārši.

• Uzziniet, ka "3" nāk sākumā.
• Diviem polinomiem vidū ir koeficienti 3.
• Atcerieties, ka jebkurš skaitlis līdz nullei ir 1. (a 0 = 1, b 0 = 1) . Ir viegli redzēt, ka formulā ir "a" pakāpes samazinājums un "b" pakāpes pieaugums. Varat to pārbaudīt:
  (a + b) 3 = a 3 b 0 + 3a 2 b 1 + 3a 1 b 2 + b 3 a 0 = a 3 + 3a 2 b + 3ab 2 + b 3

Brīdinājums!

(a + b) 3 nav vienāds ar a 3 + b 3

atšķirības kubs

Atcerieties!

atšķirības kubs divi skaitļi ir vienādi ar pirmā skaitļa kubu mīnus trīs reizes pirmā skaitļa kvadrāts un otrais plus trīs reizes pirmā skaitļa reizinājums ar otrā skaitļa kvadrātu mīnus otrā kubs.

(a - b) 3 = a 3 - 3a 2 b + 3ab 2 - b 3

Šī formula tiek atcerēta tāpat kā iepriekšējā, bet tikai ņemot vērā zīmju "+" un "-" maiņu. Pirms pirmā locekļa “a 3” ir “+” (pēc matemātikas noteikumiem mēs to nerakstām). Tas nozīmē, ka pirms nākamā dalībnieka tiks ierakstīts “-”, pēc tam atkal “+” utt.

(a − b) 3 = + a 3 - 3a 2 b + 3ab 2 - b 3 = a 3 - 3a 2 b + 3ab 2 - b 3

Kubu summa

Nejaukt ar summas kubu!

Atcerieties!

Kubu summa ir vienāds ar divu skaitļu summas reizinājumu ar starpības nepilno kvadrātu.

a 3 + b 3 = (a + b) (a 2 − ab + b 2)

Kubu summa ir divu iekavu reizinājums.

• Pirmā iekava ir divu skaitļu summa.
• Otrā iekava ir nepilnīgs skaitļu starpības kvadrāts. Nepilnīgo starpības kvadrātu sauc par izteiksmi:
  (a 2 - ab + b 2)
  Šis kvadrāts ir nepilnīgs, jo pa vidu dubultreizinājuma vietā ir parasts skaitļu reizinājums.

Kubu atšķirība

Nevajadzētu sajaukt ar atšķirības kubu!

Atcerieties!

Kubu atšķirība ir vienāds ar divu skaitļu starpības reizinājumu ar summas nepilno kvadrātu.

a 3 − b 3 = (a − b) (a 2 + ab + b 2)

Esiet piesardzīgs, rakstot rakstzīmes.

Saīsināto reizināšanas formulu pielietošana

Jāatceras, ka visas iepriekš minētās formulas tiek izmantotas arī no labās uz kreiso pusi.

Daudzi piemēri mācību grāmatās ir paredzēti, lai jūs varētu izmantot formulas, lai saliktu polinoma aizmuguri.

• a 2 + 2a + 1 = (a + 1) 2
• (ac - 4b) (ac + 4b) = a 2 c 2 - 16b 2

Jūs varat lejupielādēt tabulu ar visām saīsinātās reizināšanas formulām sadaļā "

Iepriekšējā nodarbībā mēs nodarbojāmies ar faktorizēšanu. Mēs apguvām divas metodes: kopējā faktora izņemšanu no iekavām un grupēšanu. Šajā apmācībā ir šāda efektīva metode: saīsinātās reizināšanas formulas. Īsā piezīmē - FSU.

Saīsinātās reizināšanas formulas (summas un starpības kvadrāts, summas un starpības kubs, kvadrātu starpība, kubu summa un starpība) ir būtiskas visās matemātikas nozarēs. Tos izmanto izteiksmju vienkāršošanā, vienādojumu risināšanā, polinomu reizināšanā, daļskaitļu samazināšanā, integrāļu risināšanā utt. utt. Īsāk sakot, ir viss iemesls, lai ar tiem tiktu galā. Saprast, no kurienes tie nāk, kāpēc tie ir vajadzīgi, kā tos atcerēties un kā tos pielietot.

Vai mēs saprotam?)

No kurienes nāk saīsinātās reizināšanas formulas?

Vienādības 6 un 7 nav rakstītas ļoti ierastā veidā. Tāpat kā otrādi. Tas ir ar nolūku.) Jebkura vienlīdzība darbojas gan no kreisās puses uz labo, gan no labās uz kreiso. Šādā ierakstā skaidrāk ir redzams, no kurienes nāk FSO.

Tie tiek ņemti no reizināšanas.) Piemēram:

(a+b) 2 =(a+b)(a+b)=a 2 +ab+ba+b 2 =a 2 +2ab+b 2

Tas arī viss, nekādu zinātnisku triku. Mēs vienkārši reizinām iekavas un dodam līdzīgas. Tā tas izrādās visas saīsinātās reizināšanas formulas. saīsināti reizināšana ir tāpēc, ka pašās formulās nav iekavu reizināšanas un līdzīgu redukcijas. Samazināts.) Rezultāts tiek dots uzreiz.

FSU ir jāzina no galvas. Bez pirmajiem trijiem nevar sapņot par trīskāršu, bez pārējiem - par četrinieku ar pieci.)

Kāpēc mums ir vajadzīgas saīsinātas reizināšanas formulas?

Ir divi iemesli, kāpēc šīs formulas jāmācās, pat jāiegaumē. Pirmais – gatava atbilde uz mašīnas krasi samazina kļūdu skaitu. Bet tas nav galvenais iemesls. Un, lūk, otrais...

Ja jums patīk šī vietne...

Starp citu, man jums ir vēl dažas interesantas vietnes.)

Jūs varat praktizēt piemēru risināšanu un uzzināt savu līmeni. Testēšana ar tūlītēju verifikāciju. Mācīšanās - ar interesi!)

var iepazīties ar funkcijām un atvasinājumiem.

Saīsinātās reizināšanas formulas (FSU) ir nepieciešami, lai reizinātu un palielinātu skaitļu pakāpē, izteiksmes, ieskaitot polinomus. Tas ir, ar formulu palīdzību jūs varat strādāt ar cipariem daudz ātrāk un vienkāršāk. Tādējādi no sarežģīta vienādojuma ir iespējams izveidot parastu vienādojumu, kas vienkāršos uzdevumu.

Tabula ar saīsinātām reizināšanas formulām

Vārds	Formula	Kā lasīt
summas kvadrāts		Pirmās izteiksmes kvadrāts plus divkāršs pirmās un otrās izteiksmes reizinājums, plus otrās izteiksmes kvadrāts.
Atšķirības kvadrāts		Divu izteiksmju starpības kvadrāts ir vienāds ar pirmās izteiksmes kvadrātu, mīnus divreiz pirmās izteiksmes reizinājums ar otro, plus otrās izteiksmes kvadrāts.
summas kubs		Divu izteiksmju starpības kubs ir vienāds ar pirmās izteiksmes kubu, pieskaitot trīs reizes pirmās izteiksmes reizinājumu, kas kvadrātā ar otro izteiksmi, plus trīs reizes pirmās izteiksmes reizinājumu ar otro kvadrātu, plus otro izteiksmi kubiņos.
atšķirības kubs		Divu lielumu starpības kubs ir vienāds ar pirmo izteiksmi kubā mīnus trīs reizes pirmās izteiksmes reizinājums, kas kvadrātā ar otro izteiksmi, plus trīs reizes pirmās izteiksmes reizinājums un otrā kvadrātā, atskaitot otro izteiksmi. kubiņos.
Kvadrātu atšķirība		Pirmās un otrās izteiksmes kvadrātu starpība ir vienāda ar abu izteiksmju starpības un to summas reizinājumu.
Kubu summa		Divu lielumu summas un starpības nepilnā kvadrāta reizinājums ir vienāds ar to kubu summu.
Kubu atšķirība		Divu izteiksmju starpības reizinājums ar summas nepilno kvadrātu ir vienāds ar to kubu starpību.

Pievērsiet uzmanību pirmajām četrām formulām. Pateicoties tiem, jūs varat kvadrātā vai kubā divu izteiksmju summu (starpību). Kas attiecas uz piekto formulu, tā ir jāizmanto, lai īsi reizinātu divu izteiksmju starpību vai summu.

Pēdējās divas formulas (6 un 7) tiek izmantotas, lai reizinātu abu izteiksmju summas ar to nepilnīgo kvadrātisko starpību vai summu.

Iepriekš minētās formulas praksē ir diezgan bieži vajadzīgas. Tāpēc tos vēlams zināt no galvas.

Ja jūs saskaraties ar polinoma faktorinācijas piemēru, daudzos gadījumos jums ir jāsamaina kreisā un labā puse.

Piemēram, ņemiet to pašu pirmo formulu:

un novietojiet kreiso pusi pa labi un labo pusi pa kreisi:

To pašu procedūru var veikt ar pārējām formulām.

FSU pierādījums

Pakavēsimies pie saīsināto reizināšanas formulu pierādījumiem. Tas nav grūti. Jums vienkārši jāatver kronšteini. Apsveriet pirmo formulu - summas kvadrātu:.

Pirmais solis.

Paaugstiniet a + b līdz otrajai pakāpei. Lai to izdarītu, mēs nepieskarsimies pakāpei, bet veiksim banālu reizināšanu: = x.

Otrais solis. Tagad mēs to izņemam no iekavām: x + x.

Trešais solis. Izvērsiet iekavas: x + x + x + x .

Ceturtais solis. Mēs reizinām, neaizmirstot par zīmēm: x + x +.

Piektais solis. Mēs vienkāršojam izteiksmi: .

Tādā pašā veidā var pierādīt pilnīgi jebkuru saīsinātu reizināšanas formulu.

Piemēri un risinājumi, izmantojot FSO

Parasti šīs septiņas formulas tiek izmantotas, ja jums ir jāvienkāršo izteiksme, lai atrisinātu jebkuru vienādojumu un pat izplatītu piemēru.

1. piemērs

Uzdevums

Vienkāršojiet izteicienu:

Kā redzat, pirmā saīsinātā reizināšanas formula, Sum Square, atbilst šim piemēram.

Risinājums

Pamatojoties uz pirmo formulu, ir nepieciešams sadalīt piemēru faktoros. Lai to izdarītu, mēs aplūkojam formulu un aizstājam ciparus burtu vietā. Mūsu gadījumā "a" ir 3x un "b" ir 5:

Mēs apsveram labo pusi un uzrakstām rezultātu. Mēs iegūstam:

Piemērā jums jāreizina viss reizinātais un nekavējoties jāsaņem atbilde:

Protams, ir piemēri ar daļskaitļiem. Bet, ja jūs iemācīsities atrisināt vienkāršus piemērus, jūs nebaidīsities no citiem veidiem.

2. piemērs

Uzdevums

Vienkāršojiet izteiksmi

Risinājums

= – x x + =

Šo izteiksmju dubultprodukts ir , kas sakrīt ar trinoma otro locekli (ar plus zīmi), kas nozīmē

Tātad, kā redzat, piemēros nav nekā sarežģīta. Galvenais ir zināt formulas, kur tās var pielietot un kur bez tām var iztikt.

Noderīgi avoti

1. Arefieva I. G., Piryutko O. N. Algebra: mācību grāmatu rokasgrāmata vispārējās vidējās izglītības iestāžu 7. klasei: Minska “Narodnaya Asveta”, 2017 - 304 lpp.
2. Nikolskis S. M., Potapov M. K. Algebra 7. klase: M: 2015 - 287 lpp.
3. Rubins A. G., Čulkovs P. V. Algebra. 7. klase. M: 2015 - 224 lpp.

FSU - formulas saīsinātai reizināšanai algebrā 7. klasei ar piemēriem atjaunināts: 2019. gada 22. novembrī: Zinātniskie raksti.Ru

Nodarbības saturs

Divu izteiksmju summas kvadrāts

Ir vairāki gadījumi, kad polinoma reizināšanu ar polinomu var ievērojami vienkāršot. Piemēram, tas ir gadījums (2 x+ 3y) 2 .

Izteiksme (2 x+ 3y) 2 ir divu polinomu reizinājums, no kuriem katrs ir vienāds ar (2 x+ 3y)

(2x+ 3y) 2 = (2x+ 3y)(2x+ 3y)

Mēs saņēmām polinoma reizinājumu ar polinomu. Izpildīsim to:

(2x+ 3y) 2 = (2x+ 3y)(2x+ 3y) = 4x 2 + 6xy + 6xy + 9y 2 = 4x 2 + 12xy+ 9y 2

Tas ir, izteiksme (2 x+ 3y) 2 ir vienāds ar 4x 2 + 12xy + 9y 2

(2x+ 3y) 2 = 4x 2 + 12xy+ 9y 2

Atrisināsim līdzīgu piemēru, kas ir vienkāršāks:

(a+b) 2

Izteiksme ( a+b) 2 ir divu polinomu reizinājums, no kuriem katrs ir vienāds ar ( a+b)

(a+b) 2 = (a+b)(a+b)

Veicam šo reizināšanu:

(a+b) 2 = (a+b)(a+b) = a 2 + ab + ab + b 2 = a 2 + 2ab + b 2

Tāda ir izteiciens (a+b) 2 ir vienāds ar a 2 + 2ab + b 2

(a+b) 2 = a 2 + 2ab + b 2

Izrādās, ka lieta ( a+b) 2 var pagarināt jebkuram a Un b. Pirmais piemērs, ko atrisinājām, proti (2 x+ 3y) 2 var atrisināt, izmantojot identitāti (a+b) 2 = a 2 + 2ab + b 2 . Lai to izdarītu, mainīgo vietā ir jāaizstāj a Un b atbilstošie termini no izteiksmes (2 x+ 3y) 2 . Šajā gadījumā mainīgais a spēles penis 2 x, un mainīgais b spēles penis 3 y

a = 2x

b = 3y

Un tad mēs varam izmantot identitāti (a+b) 2 = a 2 + 2ab + b 2 , bet mainīgo vietā a Un b jums ir jāaizstāj izteicieni 2 x un 3 y attiecīgi:

(2x+ 3y) 2 = (2x) 2 + 2 × 2 x× 3 y + (3y) 2 = 4x 2 + 12xy+ 9y 2

Tāpat kā pagājušajā reizē, mēs saņēmām polinomu 4x 2 + 12xy+ 9y 2 . Risinājums parasti tiek rakstīts īsāk, veicot visas elementārās pārvērtības prātā:

(2x+ 3y) 2 = 4x 2 + 12xy+ 9y 2

Identitāte (a+b) 2 = a 2 + 2ab + b 2 sauc par formulu divu izteiksmju summas kvadrātam. Šo formulu var lasīt šādi:

Divu izteiksmju summas kvadrāts ir vienāds ar pirmās izteiksmes kvadrātu, pieskaitot divreiz pirmās izteiksmes reizinājumu un otro plus otrās izteiksmes kvadrātu.

Apsveriet izteiksmi (2 + 3) 2 . To var aprēķināt divos veidos: veikt saskaitīšanu iekavās un kvadrātveida rezultātu vai izmantot formulu divu izteiksmju summas kvadrātam.

Pirmais veids:

(2 + 3) 2 = 5 2 = 25

Otrais veids:

(2 + 3) 2 = 2 2 + 2 × 2 × 3 + 3 2 = 4 + 12 + 9 = 25

2. piemērs. Pārvērst izteiksmi (5 a+ 3) 2 polinomā.

Izmantosim formulu divu izteiksmju summas kvadrātam:

(a+b) 2 = a 2 + 2ab + b 2

(5a + 3) 2 = (5a) 2 + 2 × 5 a × 3 + 3 2 = 25a 2 + 30a + 9

nozīmē, (5a + 3) 2 = 25a 2 + 30a + 9.

Mēģināsim atrisināt šo piemēru, neizmantojot summas kvadrāta formulu. Mums vajadzētu iegūt tādu pašu rezultātu:

(5a + 3) 2 = (5a + 3)(5a + 3) = 25a 2 + 15a + 15a + 9 = 25a 2 + 30a + 9

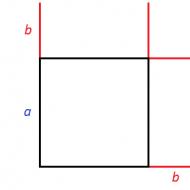
Divu izteiksmju summas kvadrāta formulai ir ģeometriska nozīme. Mēs atceramies, ka, lai aprēķinātu kvadrāta laukumu, jums jāpaaugstina tā mala līdz otrajai pakāpei.

Piemēram, kvadrāta laukums ar malu a būs vienāds ar a 2. Ja palielināsiet kvadrāta malu par b, tad laukums būs vienāds ar ( a+b) 2

Apsveriet šādu attēlu:

Iedomājieties, ka šajā attēlā redzamā kvadrāta mala ir palielināta par b. Kvadrātam visas malas ir vienādas. Ja tā puse ir palielināta par b, tad arī pārējās puses palielināsies par b

Rezultāts ir jauns kvadrāts, kas ir lielāks par iepriekšējo. Lai to labi redzētu, aizpildīsim trūkstošās puses:

Lai aprēķinātu šī kvadrāta laukumu, varat atsevišķi aprēķināt tajā iekļautos kvadrātus un taisnstūrus un pēc tam pievienot rezultātus.

Pirmkārt, jūs varat aprēķināt kvadrātu ar malu a- tā platība būs vienāda ar a 2. Tad jūs varat aprēķināt taisnstūrus ar malām a Un b- viņi būs vienādi ab. Tad jūs varat aprēķināt kvadrātu ar malu b

Rezultāts ir šāda laukumu summa:

a 2 + ab+ab + b 2

Identisku taisnstūru laukumu summu var aizstāt, reizinot ar 2 ab, kas burtiski nozīmē "atkārtot divas reizes taisnstūra ab laukumu" . Algebriski to iegūst, samazinot līdzīgus terminus ab Un ab. Rezultāts ir izteiksme a 2 + 2ab+ b 2 , kas ir divu izteiksmju summas kvadrāta formulas labā puse:

(a+b) 2 = a 2 + 2ab+ b 2

Divu izteiksmju starpības kvadrāts

Divu izteiksmju starpības kvadrāta formula ir šāda:

(a-b) 2 = a 2 − 2ab + b 2

Divu izteiksmju starpības kvadrāts ir vienāds ar pirmās izteiksmes kvadrātu, no kura atņemts divreiz pirmās izteiksmes reizinājums un otrās plus otrās izteiksmes kvadrāts.

Divu izteiksmju starpības kvadrāta formula tiek iegūta tāpat kā divu izteiksmju summas kvadrāta formula. Izteiksme ( a-b) 2 ir divu polinomu reizinājums, no kuriem katrs ir vienāds ar ( a-b)

(a-b) 2 = (a-b)(a-b)

Ja veicat šo reizināšanu, jūs iegūstat polinomu a 2 − 2ab + b 2

(a-b) 2 = (a-b)(a-b) = a 2 − ab− ab+ b 2 = a 2 − 2ab + b 2

1. piemērs. Pārvērst izteiksmi (7 x− 5) 2 uz polinomu.

Izmantosim divu izteiksmju starpības kvadrāta formulu:

(a-b) 2 = a 2 − 2ab + b 2

(7x− 5) 2 = (7x) 2–2 × 7 x × 5 + 5 2 = 49x 2 − 70x + 25

nozīmē, (7x− 5) 2 = 49x 2 + 70x + 25.

Mēģināsim atrisināt šo piemēru, neizmantojot atšķirības kvadrāta formulu. Mums vajadzētu iegūt tādu pašu rezultātu:

(7x− 5) 2 = (7x− 5) (7x− 5) = 49x 2 − 35x − 35x + 25 = 49x 2 − 70x+ 25.

Divu izteiksmju starpības kvadrāta formulai ir arī ģeometriska nozīme. Ja kvadrāta laukums ar malu a ir vienāds ar a 2, tad kvadrāta laukums, kura mala ir samazināta par b, būs vienāds ar ( a-b) 2

Apsveriet šādu attēlu:

Iedomājieties, ka šajā attēlā redzamā kvadrāta mala ir samazināta par b. Kvadrātam visas malas ir vienādas. Ja viena puse ir samazināta par b, tad arī pārējās puses samazināsies par b

Rezultāts ir jauns kvadrāts, kas ir mazāks par iepriekšējo. Attēlā tas ir iezīmēts dzeltenā krāsā. Tās puse ir a− b kopš vecās puses a samazinājies par b. Lai aprēķinātu šī kvadrāta laukumu, varat izmantot sākotnējo kvadrāta laukumu a 2 atņemiet to taisnstūru laukumus, kas iegūti vecā kvadrāta malu samazināšanas procesā. Parādīsim šos taisnstūrus:

Tad mēs varam uzrakstīt šādu izteiksmi: vecs laukums a 2 mīnus laukums ab mīnus laukums ( a-b)b

a 2 − ab − (a-b)b

Izvērsiet iekavas izteiksmē ( a-b)b

a 2 − ab - ab + b 2

Šeit ir līdzīgi termini:

a 2 − 2ab + b 2

Rezultāts ir izteiksme a 2 − 2ab + b 2 , kas ir divu izteiksmju starpības kvadrāta formulas labā puse:

(a-b) 2 = a 2 − 2ab + b 2

Parasti sauc formulas summas kvadrātam un starpības kvadrātam saīsinātās reizināšanas formulas. Šīs formulas ļauj ievērojami vienkāršot un paātrināt polinomu reizināšanas procesu.

Iepriekš teicām, ka, aplūkojot polinoma locekli atsevišķi, tas ir jāaplūko kopā ar zīmi, kas atrodas tā priekšā.

Bet, piemērojot saīsinātās reizināšanas formulas, sākotnējā polinoma zīme nav jāuzskata par paša šī termina zīmi.

Piemēram, ņemot vērā izteiksmi (5 x − 2y) 2 , un mēs vēlamies izmantot formulu (a-b) 2 = a 2 − 2ab + b 2 , tad tā vietā b nepieciešams aizstāt 2 y, nevis -2 y. Šī ir darba ar formulām iezīme, kuru nevajadzētu aizmirst.

(5x − 2y) 2
a = 5x
b = 2y
(5x − 2y) 2 = (5x) 2–2 × 5 x×2 y + (2y) 2 = 25x 2 − 20xy + 4y 2

Ja mēs aizstājam −2 y, tad tas nozīmēs, ka atšķirība sākotnējā izteiksmes iekavās ir aizstāta ar summu:

(5x − 2y) 2 = (5x + (−2y)) 2

un šajā gadījumā ir jāpiemēro nevis starpības kvadrāta formula, bet gan summas kvadrāta formula:

(5x + (−2y) 2
a = 5x
b = −2y
(5x + (−2y)) 2 = (5x) 2 + 2 × 5 x× (−2 y) + (−2y) 2 = 25x 2 − 20xy + 4y 2

Izņēmums var būt formas izteiksmes (x− (−y)) 2 . Šajā gadījumā izmantojot formulu (a-b) 2 = a 2 − 2ab + b 2 tā vietā b jāaizstāj (- y)

(x− (−y)) 2 = x 2–2 × x× (− y) + (−y) 2 = x 2 + 2xy + y 2

Bet formas izteiksmes kvadrātā x − (−y), atņemšanu būs ērtāk aizstāt ar saskaitīšanu x+y. Tad sākotnējā izteiksme būs formā ( x +y) 2 un būs iespējams izmantot summas kvadrāta formulu, nevis starpību:

(x +y) 2 = x 2 + 2xy + y 2

Summas kubs un starpības kubs

Formulas divu izteiksmju summas kubam un divu izteiksmju starpības kubam ir šādas:

(a + b) 3 = a 3 + 3a 2 b + 3ab 2 + b 3

(a-b) 3 = a 3 − 3a 2 b + 3ab 2 − b 3

Divu izteiksmju summas kuba formulu var lasīt šādi:

Divu izteiksmju summas kubs ir vienāds ar pirmās izteiksmes kubu plus trīs reizes pirmās izteiksmes kvadrāts, reiz otrais plus trīs reizes pirmās izteiksmes reizinājums ar otrās izteiksmes kvadrātu plus otrās izteiksmes kubs. izteiksme.

Un divu izteiksmju starpības kuba formulu var lasīt šādi:

Divu izteiksmju starpības kubs ir vienāds ar pirmās izteiksmes kubu, no kura atņemts trīs reizes pirmās izteiksmes kvadrāta reizinājums un otrās plus trīs reizes pirmās izteiksmes reizinājums un otrās izteiksmes kvadrāts mīnus kubs no otrās izteiksmes.

Risinot problēmas, šīs formulas vēlams zināt no galvas. Ja neatceries, tad neuztraucies! Jūs varat tos izņemt paši. Mēs jau zinām, kā.

Atvasināsim summas kuba formulu paši:

(a+b) 3

Izteiksme ( a+b) 3 ir trīs polinomu reizinājums, no kuriem katrs ir vienāds ar ( a+ b)

(a+b) 3 = (a+ b)(a+ b)(a+ b)

Bet izteiciens ( a+b) 3 var rakstīt arī kā (a+ b)(a+ b) 2

(a+b) 3 = (a+ b)(a+ b) 2

Šajā gadījumā faktors ( a+ b) 2 ir abu izteiksmju summas kvadrāts. Šis summas kvadrāts ir vienāds ar izteiksmi a 2 + 2ab + b 2 .

Tad ( a+b) 3 var uzrakstīt kā (a+ b)(a 2 + 2ab + b 2) .

(a+b) 3 = (a+ b)(a 2 + 2ab + b 2)

Un šī ir polinoma reizināšana ar polinomu. Izpildīsim to:

(a+b) 3 = (a+ b)(a 2 + 2ab + b 2) = a 3 + 2a 2 b + ab 2 + a 2 b + 2ab 2 + b 3 = a 3 + 3a 2 b + 3ab 2 + b 3

Līdzīgi varat iegūt formulu divu izteiksmju starpības kubam:

(a-b) 3 = (a- b)(a 2 − 2ab + b 2) = a 3 − 2a 2 b + ab 2 − a 2 b + 2ab 2 − b 3 = a 3 − 3a 2 b+ 3ab 2 − b 3

1. piemērs. Pārvērst izteiksmi ( x+ 1) 3 polinomā.

(a + b) 3 = a 3 + 3a 2 b + 3ab 2 + b 3

(x+ 1) 3 = x 3+3× x 2×1 + 3× x× 1 2 + 1 3 = x 3 + 3x 2 + 3x + 1

Mēģināsim atrisināt šo piemēru, neizmantojot divu izteiksmju summas kuba formulu

(x+ 1) 3 = (x+ 1)(x+ 1)(x+ 1) = (x+ 1)(x 2 + 2x + 1) = x 3 + 2x 2 + x + x 2 + 2x + 1 = x 3 + 3x 2 + 3x + 1

2. piemērs. Pārvērst izteiksmi (6a 2 + 3b 3) 3 par polinomu.

Izmantosim kuba formulu divu izteiksmju summai:

(a + b) 3 = a 3 + 3a 2 b + 3ab 2 + b 3

(6a 2 + 3b 3) 3 = (6a 2) 3 + 3 × (6 a 2) 2 × 3 b 3+3×6 a 2 × (3b 3) 2 + (3b 3) 3 = 216a 6+3×36 a 4 × 3 b 3+3×6 a 2×9 b 6 + 27b 9

3. piemērs. Pārvērst izteiksmi ( n 2 − 3) 3 polinomā.

(a-b) = a 3 − 3a 2 b + 3ab 2 − b 3

(n 2 − 3) 3 = (n 2) 3–3 × ( n 2) 2 × 3 + 3 × n 2 × 3 2 - 3 3 = n 6 − 9n 4 + 27n 2 − 27

4. piemērs. Pārvērst izteiksmi (2x 2 − x 3) 3 par polinomu.

Izmantosim divu izteiksmju starpības kuba formulu:

(a-b) = a 3 − 3a 2 b + 3ab 2 − b 3

(2x 2 − x 3) 3 = (2x 2) 3–3 × (2 x 2) 2 × x 3+3×2 x 2×( x 3) 2 − (x 3) 3 =
8x 6–3 × 4 x 4× x 3+3×2 x 2× x 6 − x 9 =
8x 6 − 12x 7 + 6x 8 − x 9

Reizinot divu izteiksmju starpību ar to summu

Ir problēmas, kurās ir jāreizina divu izteiksmju starpība ar to summu. Piemēram:

(a-b)(a+b)

Šajā izteiksmē divu izteiksmju atšķirība a Un b reizināts ar to pašu divu izteiksmju summu. Veicam šo reizināšanu:

(a-b)(a+b) = a 2 + ab − ab − b 2 = a 2 − b 2

Tāda ir izteiciens (a-b)(a+b) vienāds a 2 − b 2

(a-b)(a+b) = a 2 − b 2

Mēs redzam, ka, reizinot divu izteiksmju starpību ar to summu, mēs iegūstam šo izteiksmju kvadrātu starpību.

Divu izteiksmju starpības un to summas reizinājums ir vienāds ar šo izteiksmju kvadrātu starpību.

Notiek (a-b)(a+b) var attiecināt uz jebkuru a Un b. Vienkārši sakot, ja, risinot uzdevumu, ir jāreizina divu izteiksmju starpība ar to summu, tad šo reizinājumu var aizstāt ar šo izteiksmju kvadrātu starpību.

1. piemērs. Veikt reizināšanu (2x − 5)(2x + 5)

Šajā piemērā izteiksmes atšķirība ir 2 x un 5 reizināts ar šo pašu izteiksmju summu. Tad pēc formulas (a-b)(a+b) = a 2 − b 2 mums ir:

(2x − 5)(2x + 5) = (2x) 2 − 5 2

Mēs aprēķinām labo pusi, mēs iegūstam 4 x 2 − 25

(2x − 5)(2x + 5) = (2x) 2 − 5 2 = 4x 2 − 25

Mēģināsim atrisināt šo piemēru, neizmantojot formulu (a-b)(a+b) = a 2 − b 2 . Mēs iegūsim tādu pašu rezultātu 4 x 2 − 25

(2x − 5)(2x + 5) = 4x 2 − 10x + 10x − 25 = 4x 2 − 25

2. piemērs. Veikt reizināšanu (4x − 5y)(4x + 5y)

(a-b)(a+b) = a 2 − b 2

(4x − 5y)(4x + 5y) = (4x) 2 − (5y) 2 = 16x 2 − 25y 2

3. piemērs. Veikt reizināšanu (2a+ 3b)(2a− 3b)

Izmantosim formulu divu izteiksmju starpības reizināšanai ar to summu:

(a-b)(a+b) = a 2 − b 2

(2a + 3b)(2a- 3b) = (2a) 2 − (3b) 2 = 4a 2 − 9b 2

Šajā piemērā terminu summa ir 2 a un 3 b atrodas agrāk nekā šo terminu atšķirība. Un formulā (a-b)(a+b) = a 2 − b 2 atšķirība atrodas agrāk.

Nav nozīmes tam, kā faktori ir sakārtoti ( a-b) iekšā ( a+b) formulā. Tos var rakstīt kā (a-b)(a+b) , un (a+b)(a-b) . Rezultāts joprojām būs a 2 − b 2, jo reizinājums nemainās no faktoru permutācijas.

Tātad šajā piemērā faktori (2 a + 3b) un 2 a- 3b) var rakstīt kā (2a + 3b)(2a- 3b) , un (2a- 3b)(2a + 3b) . Rezultāts joprojām būs 4. a 2 − 9b 2 .

3. piemērs. Veikt reizināšanu (7 + 3x)(3x − 7)

Izmantosim formulu divu izteiksmju starpības reizināšanai ar to summu:

(a-b)(a+b) = a 2 − b 2

(7 + 3x)(3x − 7) = (3x) 2 − 7 2 = 9x 2 − 49

4. piemērs. Veikt reizināšanu (x 2 − y 3)(x 2 + y 3)

(a-b)(a+b) = a 2 − b 2

(x 2 − y 3)(x 2 + y 3) = (x 2) 2 − (y 3) 2 = x 4 − y 6

5. piemērs. Veikt reizināšanu (−5x− 3y)(5x− 3y)

Izteiksmē (-5 x− 3y) izņemam −1, tad sākotnējai izteiksmei būs šāda forma:

(−5x− 3y)(5x− 3y) = −1(5x + 3y)(5x − 3y)

Darbs (5x + 3y)(5x − 3y) aizstāt ar kvadrātu starpību:

(−5x− 3y)(5x− 3y) = −1(5x + 3y)(5x − 3y) = −1((5x) 2 − (3y) 2)

Kvadrātu atšķirības tika ievietotas iekavās. Ja tas nav izdarīts, izrādīsies, ka −1 tiek reizināts tikai ar (5 x) 2 . Un tas novedīs pie kļūdas un mainīs sākotnējās izteiksmes vērtību.

(−5x− 3y)(5x− 3y) = −1(5x + 3y)(5x − 3y) = −1((5x) 2 − (3y) 2) = −1(25x 2 − 9x 2)

Tagad reiziniet −1 ar izteiksmi iekavās un iegūstiet gala rezultātu:

(−5x− 3y)(5x− 3y) = −1(5x + 3y)(5x − 3y) = −1((5x) 2 − (3y) 2) =
−1(25x 2 − 9y 2) = −25x 2 + 9y 2

Reizinot divu izteiksmju starpību ar to summas nepilno kvadrātu

Ir problēmas, kurās divu izteiksmju starpība ir jāreizina ar to summas nepilno kvadrātu. Šis gabals izskatās šādi:

(a-b)(a 2 + ab + b 2)

Pirmais polinoms ( a-b) ir divu izteiksmju un otrā polinoma atšķirība (a 2 + ab + b 2) ir šo divu izteiksmju summas nepilnīgs kvadrāts.

Summas nepilnīgais kvadrāts ir formas polinoms a 2 + ab + b 2 . Tas ir līdzīgs parastajam summas kvadrātam a 2 + 2ab + b 2

Piemēram, izteiksme 4x 2 + 6xy + 9y 2 ir izteiksmju summas 2 nepilnīgs kvadrāts x un 3 y .

Patiešām, izteiciena pirmais termins 4x 2 + 6xy + 9y 2 , proti, 4 x 2 ir izteiksmes 2 kvadrāts x, kopš (2 x) 2 = 4x 2. Trešais izteiksmes termins 4x 2 + 6xy + 9y 2 , proti, 9 y 2 ir kvadrāts no 3 y, jo (3 y) 2 = 9y 2. vidējais penis 6 xy, ir 2. izteiksmes reizinājums x un 3 y.

Tātad reizināsim starpību ( a-b) ar nepilnu summas kvadrātu a 2 + ab + b 2

(a-b)(a 2 + ab + b 2) = a(a 2 + ab + b 2) − b(a 2 + ab + b 2) =
a 3 + a 2 b + ab 2 − a 2 b − ab 2 − b 3 = a 3 − b 3

Tāda ir izteiciens (a-b)(a 2 + ab + b 2) vienāds a 3 − b 3

(a-b)(a 2 + ab + b 2) = a 3 − b 3

Šo identitāti sauc par formulu divu izteiksmju starpības reizināšanai ar to summas nepilnīgo kvadrātu. Šo formulu var lasīt šādi:

Divu izteiksmju starpības un to summas nepilnā kvadrāta reizinājums ir vienāds ar šo izteiksmju kubu starpību.

1. piemērs. Veikt reizināšanu (2x − 3y)(4x 2 + 6xy + 9y 2)

Pirmais polinoms (2 x − 3y) ir divu izteiksmju atšķirība 2 x un 3 y. Otrais polinoms 4x 2 + 6xy + 9y 2 ir divu izteiksmju summas nepilnīgs kvadrāts 2 x un 3 y. Tas ļauj izmantot formulu, neveicot garus aprēķinus (a-b)(a 2 + ab + b 2) = a 3 − b 3 . Mūsu gadījumā reizināšana (2x − 3y)(4x 2 + 6xy + 9y 2) var aizstāt ar kubu starpību 2 x un 3 y

(2x − 3y)(4x 2 + 6xy + 9y 2) = (2x) 3 − (3y) 3 = 8x 3 − 27y 3

(a-b)(a 2 + ab+ b 2) = a 3 − b 3 . Mēs iegūstam tādu pašu rezultātu, bet risinājums kļūst garāks:

(2x − 3y)(4x 2 + 6xy + 9y 2) = 2x(4x 2 + 6xy + 9y 2) − 3y(4x 2 + 6xy + 9y 2) =
8x 3 + 12x 2 y + 18xy 2 − 12x 2 y − 18xy 2 − 27y 3 = 8x 3 − 27y 3

2. piemērs. Veikt reizināšanu (3 − x)(9 + 3x + x 2)

Pirmais polinoms (3 - x) ir abu izteiksmju atšķirība, un otrais polinoms ir šo divu izteiksmju summas nepilnais kvadrāts. Tas ļauj mums izmantot formulu (a-b)(a 2 + ab + b 2) = a 3 − b 3

(3 − x)(9 + 3x + x 2) = 3 3 − x 3 = 27 − x 3

Divu izteiksmju summas reizināšana ar to starpības nepilno kvadrātu

Ir problēmas, kurās divu izteiksmju summa jāreizina ar to starpības nepilno kvadrātu. Šis gabals izskatās šādi:

(a+b)(a 2 − ab + b 2)

Pirmais polinoms ( a+b (a 2 − ab + b 2) ir nepilnīgs šo divu izteiksmju atšķirības kvadrāts.

Nepilnīgais starpības kvadrāts ir formas polinoms a 2 − ab + b 2 . Tas ir līdzīgs parastajai atšķirībai kvadrātā a 2 − 2ab + b 2 izņemot to, ka tajā pirmās un otrās izteiksmes reizinājums nav dubultots.

Piemēram, izteiksme 4x 2 − 6xy + 9y 2 ir nepilnīgs izteiksmju starpības kvadrāts 2 x un 3 y .

(2x) 2 − 2x× 3 y + (3y) 2 = 4x 2 − 6xy + 9y 2

Atgriezīsimies pie sākotnējā piemēra. Sareizināsim summu a+b ar starpības nepilno kvadrātu a 2 − ab + b 2

(a+b)(a 2 − ab + b 2) = a(a 2 − ab + b 2) + b(a 2 − ab + b 2) =
a 3 − a 2 b + ab 2 + a 2 b − ab 2 + b 3 = a 3 + b 3

Tāda ir izteiciens (a+b)(a 2 − ab + b 2) vienāds a 3 + b 3

(a+b)(a 2 − ab + b 2) = a 3 + b 3

Šo identitāti sauc par formulu divu izteiksmju summas reizināšanai ar to starpības nepilnīgo kvadrātu. Šo formulu var lasīt šādi:

Divu izteiksmju summas un to starpības nepilnā kvadrāta reizinājums ir vienāds ar šo izteiksmju kubu summu.

1. piemērs. Veikt reizināšanu (2x + 3y)(4x 2 − 6xy + 9y 2)

Pirmais polinoms (2 x + 3y) ir divu izteiksmju summa 2 x un 3 y, un otrais polinoms 4x 2 − 6xy + 9y 2 ir šo izteiksmju starpības nepilnīgais kvadrāts. Tas ļauj izmantot formulu, neveicot garus aprēķinus (a+b)(a 2 − ab + b 2) = a 3 + b 3 . Mūsu gadījumā reizināšana (2x + 3y)(4x 2 − 6xy + 9y 2) var aizstāt ar kubu summu 2 x un 3 y

(2x + 3y)(4x 2 − 6xy + 9y 2) = (2x) 3 + (3y) 3 = 8x 3 + 27y 3

Mēģināsim atrisināt to pašu piemēru, neizmantojot formulu (a+b)(a 2 − ab+ b 2) = a 3 + b 3 . Mēs iegūstam tādu pašu rezultātu, bet risinājums kļūst garāks:

(2x + 3y)(4x 2 − 6xy + 9y 2) = 2x(4x 2 − 6xy + 9y 2) + 3y(4x 2 − 6xy + 9y 2) =
8x 3 − 12x 2 y + 18xy 2 + 12x 2 y − 18xy 2 + 27y 3 = 8x 3 + 27y 3

2. piemērs. Veikt reizināšanu (2x+ y)(4x 2 − 2xy + y 2)

Pirmais polinoms (2 x+ y) ir divu izteiksmju un otrā polinoma summa (4x 2 − 2xy + y 2) ir šo izteiksmju atšķirības nepilnīgs kvadrāts. Tas ļauj mums izmantot formulu (a+b)(a 2 − ab+ b 2) = a 3 + b 3

(2x+ y)(4x 2 − 2xy + y 2) = (2x) 3 + y 3 = 8x 3 + y 3

Mēģināsim atrisināt to pašu piemēru, neizmantojot formulu (a+b)(a 2 − ab+ b 2) = a 3 + b 3 . Mēs iegūstam tādu pašu rezultātu, bet risinājums kļūst garāks:

(2x+ y)(4x 2 − 2xy + y 2) = 2x(4x 2 − 2xy + y 2) + y(4x 2 − 2xy + y 2) =
8x 3 − 4x 2 y + 2xy 2 + 4x 2 y − 2xy 2 + y 3 = 8x 3 + y 3

Uzdevumi patstāvīgam risinājumam

Vai jums patika nodarbība?
Pievienojieties mūsu jaunajai Vkontakte grupai un sāciet saņemt paziņojumus par jaunām nodarbībām

>>Math: samazinātas reizināšanas formulas

Saīsinātās reizināšanas formulas

Ir vairāki gadījumi, kad viena polinoma reizināšana ar citu rada kompaktu, viegli iegaumējamu rezultātu. Šādos gadījumos ir vēlams nereizināt katru reizi polinoms no otras puses, un izmantojiet gatavo rezultātu. Apskatīsim šos gadījumus.

1. Summas kvadrāts un starpības kvadrāts:

1. piemērs Atvērt iekavas izteiksmē:

a) (3x + 2) 2 ;

b) (5.a 2.–4.b 3.) 2

a) Mēs izmantojam formulu (1),ņemot vērā, ka a lomu spēlē 3x, bet b lomu spēlē skaitlis 2.
Mēs iegūstam:

(Zx + 2) 2 = (3x) 2 + 2 Zx 2 + 2 2 = 9x 2 + 12x + 4.

b) Mēs izmantojam formulu (2), ņemot vērā, ka lomā bet runā 5a 2, un lomā b runā 4b 3. Mēs iegūstam:

(5a 2-4b 3) 2 \u003d (5a 2) 2 - 2- 5a 2 4b 3 + (4b 3) 2 = 25a 4 -40a 2 b 3 + 16b 6.

Lietojot formulas summas kvadrātam vai starpības kvadrātam, paturiet to prātā
(- a - b) 2 \u003d (a + b) 2;
(b-a) 2 = (a-b) 2 .

Tas izriet no fakta, ka (- a) 2 = a 2 .

Ņemiet vērā, ka daži matemātiskie triki ir balstīti uz formulām (1) un (2), ļaujot jums veikt aprēķinus savā galvā.

Piemēram, var praktiski verbāli kvadrātā skaitļus, kas beidzas ar 1 un 9. Patiešām

71 2 = (70 + 1) 2 = 70 2 + 2 70 1 + 1 2 = 4900 + 140 + 1 = 5041;
91 2 = (90 + I) 2 = 90 2 + 2 90 1 + 1 2 = 8100 + 180 + 1 = 8281;
69 2 \u003d (70 - I) 2 \u003d 70 2 - 2 70 1 + 1 2 = 4900 - 140 + 1 = 4761.

Dažreiz jūs varat arī ātri izvilkt kvadrātā skaitli, kas beidzas ar 2 vai 8. Piemēram,

102 2 = (100 + 2) 2 = 100 2 + 2 100 2 + 2 2 = 10 000 + 400 + 4 = 10 404;

48 2 = (50 - 2) 2 = 50 2 - 2 50 2 + 2 2 = 2500 - 200 + 4 = 2304.

Bet elegantākais triks ir skaitļu, kas beidzas ar 5, kvadrātā.
Veiksim atbilstošo argumentāciju 85 2 .

Mums ir:

85 2 = (80 + 5) 2 = 80 2 + 2 80 5 + 5 2 =-80 (80+ 10)+ 25 = 80 90 + 25 = 7200 + 25 = 7225.

Mēs atzīmējam, ka, lai aprēķinātu 85 2, bija pietiekami reizināt 8 ar 9 un iegūtajam rezultātam pievienot 25. Tāpat jūs varat darīt to pašu citos gadījumos. Piemēram, 35 2 \u003d 1225 (3 4 \u003d 12 un 25 tika pievienots iegūtajam skaitlim labajā pusē);

65 2 = 4225; 1252 \u003d 15625 (12 18 \u003d 156 un 25 tika pievienots iegūtajam skaitlim labajā pusē).

Tā kā mēs runājam par dažādiem kurioziem apstākļiem, kas saistīti ar garlaicīgām (no pirmā acu uzmetiena) formulām (1) un (2), mēs šo sarunu papildināsim ar šādu ģeometrisko argumentāciju. Lai a un b ir pozitīvi skaitļi. Aplūkosim kvadrātu ar malu a + b un divos tā stūros izgriežam kvadrātus, kuru malas ir vienādas ar a un b (4. att.).

Kvadrāta laukums ar malu a + b ir (a + b) 2 . Bet mēs sagriežam šo kvadrātu četrās daļās: kvadrāts ar malu a (tā laukums ir a 2), kvadrāts ar malu b (tā laukums ir b 2), divi taisnstūri ar malām a un b (katra tāda laukums taisnstūris ir ab). Tādējādi (a + b) 2 = a 2 + b 2 + 2ab, t.i., esam ieguvuši formulu (1).

Reiziniet binomiālu a + b ar binomiālu a - b. Mēs iegūstam:
(a + b) (a - b) \u003d a 2 - ab + ba - b 2 \u003d a 2 - b 2.
tātad

Jebkuru vienlīdzību matemātikā izmanto gan no kreisās puses uz labo (t.i., vienādības kreiso pusi aizstāj ar tās labo pusi), gan no labās uz kreiso (t.i., vienādības labā puse tiek aizstāta ar tās kreiso pusi). Ja formulu C) izmanto no kreisās uz labo pusi, tad tā ļauj aizstāt produktu (a + b) (a - b) ar gatavo rezultātu a 2 - b 2 . To pašu formulu var izmantot no labās puses uz kreiso, tad tā ļauj aizstāt kvadrātu starpību a 2 - b 2 ar reizinājumu (a + b) (a - b). Formulai (3) matemātikā dots īpašs nosaukums – kvadrātu atšķirība.

komentēt. Nejauciet jēdzienus "kvadrātu starpība" ar un "starpība kvadrātā". Kvadrātu atšķirība ir a 2 - b 2, kas nozīmē, ka mēs runājam par formulu (3); starpības kvadrāts ir (a-b) 2, tāpēc mēs runājam par formulu (2). Parastā valodā formulu (3) lasa "no labās uz kreiso" šādi:

divu skaitļu (izteiksmju) kvadrātu starpība ir vienāda ar šo skaitļu (izteiksmju) summas un to starpības reizinājumu,

2. piemērs Veikt reizināšanu

(3x-2g) (3x+2g)
Risinājums. Mums ir:
(3x - 2g) (3x + 2g) \u003d (3x) 2 - (2g) 2 \u003d 9x 2 - 4y 2.

3. piemērs Izsakiet binomiālu 16x4 - 9 kā binomiālu reizinājumu.

Risinājums. Mums ir: 16x 4 \u003d (4x 2) 2, 9 \u003d Z 2, kas nozīmē, ka dotais binoms ir kvadrātu starpība, t.i. tai var piemērot formulu (3), lasīt no labās uz kreiso pusi. Tad mēs iegūstam:

16 x 4–9 = (4 x 2) 2 – W 2 = (4 x 2 + 3) (4 x 2 –3)

Formula (3), tāpat kā formulas (1) un (2), tiek izmantota matemātiskiem trikiem. Skatīt:

79 81 = (80 - 1) (80 + 1) - 802 - I2 = 6400 - 1 = 6399;
42 38 = D0 + 2) D0 - 2) = 402 - 22 = 1600 - 4 = 1596.

Pabeigsim sarunu par kvadrātu atšķirības formulu ar ziņkārīgu ģeometrisku argumentāciju. Lai a un b ir pozitīvi skaitļi, kur a > b. Aplūkosim taisnstūri ar malām a + b un a - b (5. att.). Tās laukums ir (a + b) (a - b). Izgrieziet taisnstūri ar malām b un a - b un pielīmējiet to atlikušajai daļai, kā parādīts 6. attēlā. Ir skaidrs, ka iegūtajam skaitlim ir vienāds laukums, t.i. (a + b) (a - b). Bet šis skaitlis var
veidot šādi: no kvadrāta ar malu a izgriež kvadrātu ar malu b (tas labi redzams 6. att.). Tātad jaunās figūras laukums ir 2-b 2. Tātad, (a + b) (a - b) \u003d a 2 - b 2, t.i., mēs saņēmām formulu (3).

3. Kubu starpība un kubu summa

Reiziniet binomiālu a - b ar trinomu a 2 + ab + b 2.
Mēs iegūstam:
(a - b) (a 2 + ab + b 2) \u003d a a 2 + a ab + a b 2 - b a 2 - b ab -bb 2 \u003d a 3 + a 2 b + ab 2 -a 2 b- ab 2 -b 3 = 3 -b 3.

Līdzīgi

(a + b) (a 2 - ab + b 2) = a 3 + b 3

(pārbaudi pats). Tātad,

Formulu (4) parasti sauc kubu atšķirība, formula (5) - kubu summa. Mēģināsim pārtulkot formulas (4) un (5) parastajā valodā. Pirms to izdarīt, ņemiet vērā, ka izteiksme a 2 + ab + b 2 ir līdzīga izteiksmei a 2 + 2ab + b 2, kas parādījās formulā (1) un deva (a + b) 2 ; izteiksme a 2 - ab + b 2 ir līdzīga izteiksmei a 2 - 2ab + b 2, kas parādījās formulā (2) un deva (a - b) 2 .

Lai atšķirtu (valodā) šos izteiksmju pārus vienu no otra, katru no izteiksmēm a 2 + 2ab + b 2 un a 2 - 2ab + b 2 sauc par perfektu kvadrātu (summu vai starpību), un katru no izteiksmēm a 2 + ab + b 2 un a 2 - ab + b 2 sauc par nepilnu kvadrātu (summu vai starpību). Tad mēs iegūstam šādu (4) un (5) formulu (lasiet "no labās uz kreiso") tulkojumu parastajā valodā:

divu skaitļu (izteiksmju) kubu starpība ir vienāda ar šo skaitļu (izteiksmju) starpības reizinājumu ar to summas nepilno kvadrātu; divu skaitļu (izteiksmju) kubu summa ir vienāda ar šo skaitļu (izteiksmju) summas reizinājumu ar to starpības nepilno kvadrātu.

komentēt. Visas šajā sadaļā iegūtās formulas (1)-(5) tiek izmantotas gan no kreisās uz labo, gan no labās uz kreiso, tikai pirmajā gadījumā (no kreisās uz labo) saka, ka (1)-(5) ir saīsināta reizināšana. formulas, un otrajā gadījumā (no labās uz kreiso) viņi saka, ka (1)-(5) ir faktorizācijas formulas.

4. piemērs Reiziniet (2x-1) (4x2 + 2x+1).

Risinājums. Tā kā pirmais faktors ir starpība starp monomiem 2x un 1, bet otrais ir to summas nepilnīgais kvadrāts, tad var izmantot formulu (4). Mēs iegūstam:

(2x - 1) (4x 2 + 2x + 1) \u003d (2x) 3 - I 3 \u003d 8x 3 - 1.

5. piemērs Izsakiet binomiālu 27a 6 + 8b 3 kā polinomu reizinājumu.

Risinājums. Mums ir: 27а 6 = (2) 3 , 8b 3 = (2b) 3 . Tas nozīmē, ka dotais binomiāls ir kubu summa, t.i., tam var piemērot formulu 95), lasot no labās uz kreiso pusi. Tad mēs iegūstam:

27a 6 + 8b 3 = (2) 3 + (2b) 3 = (2 + 2b) ((2) 2 - 2 2b + (2b) 2) = (2 + 2b) (9a 4 - 6a 2 b + 4b 2).

Palīdzība skolēnam tiešsaistē, Matemātika 7. klasei lejupielāde, kalendāra tematiskā plānošana

A. V. Pogorelovs, Ģeometrija 7.-11.klasei, Mācību grāmata izglītības iestādēm

Nodarbības saturs nodarbības kopsavilkums atbalsta rāmis nodarbības prezentācijas akseleratīvas metodes interaktīvās tehnoloģijas Prakse uzdevumi un vingrinājumi pašpārbaudes darbnīcas, apmācības, lietas, uzdevumi mājasdarbi diskusijas jautājumi retoriski jautājumi no studentiem Ilustrācijas audio, video klipi un multivide fotogrāfijas, attēli, grafika, tabulas, shēmas, humors, anekdotes, joki, komiksi līdzības, teicieni, krustvārdu mīklas, citāti Papildinājumi tēzes raksti mikroshēmas zinātkāriem apkrāptu lapas mācību grāmatas pamata un papildu terminu glosārijs cits Mācību grāmatu un stundu pilnveidošanakļūdu labošana mācību grāmatā Inovācijas elementu fragmenta atjaunošana mācību grāmatā mācību stundā novecojušo zināšanu aizstāšana ar jaunām Tikai skolotājiem ideālas nodarbības kalendārais plāns gadam diskusiju programmas metodiskie ieteikumi Integrētās nodarbības

Facebook

Twitter

Saskarsmē ar

klasesbiedriem

Google+