省略されたキューブ乗算の例。 省略された乗算式。 例を含む詳細な理論。 多項式による多項式の乗算
代数多項式を計算するとき、計算を単純化するために、 省略された乗算式。 全部で7つのそのような公式があります。 それらはすべて心から知る必要があります。
また、数式に「a」と「b」の代わりに、数値と他の代数多項式の両方が存在する可能性があることも覚えておく必要があります。
二乗の差
覚えて!
二乗の差 2つの数値は、これらの数値の差とそれらの合計の積に等しくなります。
a 2 − b 2 =(a − b)(a + b)- 15 2 − 2 2 =(15 − 2)(15 + 2)= 13 17 = 221
- 9a 2 − 4b 2、2 =(3a − 2bc)(3a + 2bc)
合計二乗
覚えて!
2つの数値の合計の二乗は、最初の数値の二乗に最初の数値と2番目の数値の積の2倍を加えたものに、2番目の数値の二乗を加えたものに等しくなります。
(a + b)2 = a 2 + 2ab + b 2
この縮小された乗算式を使用すると、次のことが簡単になります。 大きな数の正方形を見つける電卓や長い掛け算を使わずに。 例を挙げて説明しましょう。
1122を検索します。
- 112を、よく覚えている平方数の合計に分解してみましょう。
112 = 100 + 1 - 数字の合計を角かっこで囲み、角かっこの上に正方形を置きます。
112 2 = (100 + 12) 2 - 合計二乗式を使用してみましょう:
112 2 =(100 + 12)2 = 100 2 + 2100 12 + 12 2 = 10,000 + 2,400 + 144 = 12,544
二乗和の公式は、すべての代数多項式にも有効であることに注意してください。
- (8a + c)2 = 64a 2 + 16ac + c 2
警告!
(a + b)2は(a 2 + b 2)と等しくありません差の二乗
覚えて!
2つの数値の差の二乗は、最初の数値の二乗から、最初と2番目の積の2倍を引いたものに、2番目の数値の二乗を加えたものに等しくなります。
(a − b)2 = a 2 − 2ab + b 2
非常に便利な変換を覚えておくことも価値があります。
(a --b)2 =(b --a)2上記の式は、括弧を展開するだけで証明されます。
(a − b)2 = a 2 −2ab + b 2 = b 2 − 2ab + a 2 =(b − a)2合計キューブ
覚えて!
2つの数値の合計の立方体は、最初の数値の3乗に、最初の数値の2乗の3倍に2番目の数値を掛けたものに、1番目の2乗の2乗と2番目の3乗の積の3倍を加えたものに等しくなります。
(a + b)3 = a 3 + 3a 2 b + 3ab 2 + b 3
合計キューブを覚える方法
この「ひどい」見た目の式を覚えているのは非常に簡単です。
- 「a3」が最初に来ることを学びます。
- 中央の2つの多項式の係数は3です。
- ゼロ乗の任意の数は1であることを思い出してください。 (a 0 = 1、b 0 = 1)。 式では、次数「a」が減少し、次数「b」が増加していることが簡単にわかります。 これを確認できます:
(a + b)3 = a 3 b 0 + 3a 2 b 1 + 3a 1 b 2 + b 3 a 0 = a 3 + 3a 2 b + 3ab 2 + b 3
警告!
(a + b)3はa 3 + b3と等しくありません差分キューブ
覚えて!
差分キューブ 2つの数値は、最初の数値の3乗から最初の数値の2乗の3倍に2番目の数値を掛けたものに、最初の数値の積に2番目の2乗を掛けたものから2番目の3乗を引いたものに等しくなります。
(a − b)3 = a 3 − 3a 2 b + 3ab 2 − b 3
この式は前の式と同じように記憶されていますが、記号「+」と「-」の交互を考慮に入れているだけです。 最初のメンバー「a3」の前に「+」があります(数学の規則に従って、私たちはそれを書きません)。 これは、次のメンバーの前に「-」、次に「+」などが続くことを意味します。
(a − b)3 = + a 3-3a 2 b + 3ab 2-b 3 = a 3-3a 2 b + 3ab 2-b 3立方体の合計
合計キューブと混同しないでください!
覚えて!
立方体の合計差の不完全な二乗による2つの数値の合計の積に等しい。
a 3 + b 3 =(a + b)(a 2 − ab + b 2)立方体の合計は、2つの括弧の積です。
- 最初の括弧は2つの数値の合計です。
- 2番目の括弧は、数値の差の不完全な2乗です。 差の不完全な二乗は、次の式と呼ばれます。
(a 2 − ab + b 2)
この正方形は不完全です。なぜなら、真ん中には二重の積ではなく、通常の数の積があるからです。
キューブの違い
差分キューブと混同しないでください!
覚えて!
キューブの違いは、2つの数値の差と、合計の不完全な2乗の積に等しくなります。
a 3 − b 3 =(a − b)(a 2 + ab + b 2)文字を書くときは注意してください。
省略された乗算式の適用
上記のすべての式も右から左に使用されていることを覚えておく必要があります。
教科書の多くの例は、数式を使用して多項式を組み立て戻すように設計されています。
- a 2 + 2a + 1 =(a + 1)2
- (ac − 4b)(ac + 4b)= a 2 c 2 − 16b 2
「」のセクションで、省略された乗算のすべての式を含む表をダウンロードできます。
前のレッスンでは、因数分解について説明しました。 私たちは2つの方法を習得しました:括弧から共通の要素を取り除くこととグループ化です。 このチュートリアルでは、次の強力な方法を使用します。 省略された乗算式。 簡単に言えば-FSU。
簡略化された乗算式(合計と差の2乗、合計と差の3乗、2乗の差、3乗の合計と差)は、数学のすべての分野で不可欠です。 これらは、式の簡略化、方程式の解法、多項式の乗算、分数の削減、積分の解法などで使用されます。 等 要するに、それらに対処する理由はすべてあります。 それらがどこから来たのか、なぜそれらが必要なのか、それらを覚える方法、そしてそれらを適用する方法を理解してください。
分かりますか?)
省略された乗算式はどこから来ますか?
等式6と7は、ごく普通の方法で書かれていません。 反対のように。 これは意図的なものです。)平等は、左から右、右から左の両方で機能します。 このような記録では、FSOがどこから来ているのかが明確になっています。
それらは乗算から取得されます。)例:
(a + b)2 =(a + b)(a + b)= a 2 + ab + ba + b 2 = a 2 + 2ab + b 2
それだけです、科学的なトリックはありません。 角かっこを掛けて、同じようなものを与えます。 これが結果です すべての省略された乗算式。 省略形乗算は、数式自体に括弧の乗算や類似の括弧の縮小がないためです。 削減されました。)結果はすぐに表示されます。
FSUは心から知る必要があります。 最初の3つがなければ、残りがなければトリプルを夢見ることはできません。
なぜ省略された乗算式が必要なのですか?
これらの公式を学び、覚える理由は2つあります。 1つ目は、マシン上の既成の回答により、エラーの数が大幅に減少します。 しかし、これが主な理由ではありません。 そして、これが2番目です...
あなたがこのサイトが好きなら...
ちなみに、もっと面白いサイトがいくつかあります。)
例を解く練習をして、自分のレベルを知ることができます。 即時検証によるテスト。 学習-興味を持って!)
関数と導関数に精通することができます。
省略された乗算式(FSU)多項式を含む数、式を乗算して累乗するために必要です。 つまり、数式を使用すると、数値をはるかに速く簡単に操作できます。 したがって、複雑な方程式から常微分方程式を作成することが可能であり、これによりタスクが簡略化されます。
乗算式を省略した表
| 名前 | 方式 | 読み方 |
|---|---|---|
| 合計二乗 | 最初の式の2乗に、1番目と2番目の式の積の2倍を加えたものに、2番目の式の2乗を加えたもの。 | |
| 差の二乗 | 2つの式の差の二乗は、最初の式の二乗から、最初の式と2番目の式の積の2倍を引いたものに、2番目の式の二乗を加えたものに等しくなります。 | |
| 合計キューブ | 2つの式の差の立方体は、最初の式の3乗に2番目の式を2乗した最初の式の積の3倍、2番目の式を2乗した最初の式の積の3倍、および2番目の式を加えたものに等しくなります。立方体。 | |
| 差分キューブ | 2つの量の差の立方体は、立方体の最初の式から2番目の式を2乗した最初の式の積の3倍に、最初の式と2番目の2乗の積の3倍を引いたものから2番目の式を引いたものに等しくなります。立方体。 | |
| 二乗の差 | 1番目と2番目の式の二乗の差は、2つの式の差とそれらの合計の積に等しくなります。 | |
| 立方体の合計 | 2つの量の合計と差の不完全な二乗の積は、それらの3乗の合計に等しくなります。 | |
| キューブの違い | 合計の不完全な二乗による2つの式の差の積は、それらの3乗の差に等しくなります。 |
最初の4つの式に注意してください。 それらのおかげで、2つの式の合計(差)を2乗または3乗することができます。 5番目の式については、2つの式の差または合計を簡単に乗算するために使用する必要があります。
最後の2つの式(6と7)は、両方の式の合計に、不完全な2乗の差または合計を掛けるために使用されます。
上記の式は、実際には非常に頻繁に必要になります。 そのため、それらを心から知ることが望ましいのです。
多項式の因数分解の例に出くわした場合、多くの場合、左側と右側を入れ替える必要があります。
たとえば、同じ最初の式を取ります。
左側を右側に、右側を左側に配置します。
残りの数式でも同じ手順を実行できます。
FSUプルーフ
省略された乗算式の証明について詳しく見ていきましょう。 これは難しいことではありません。 角かっこを開くだけです。 最初の式、つまり合計の2乗を考えてみましょう。
第一歩。
a + bを2乗します。 これを行うには、次数には触れませんが、平凡な乗算を実行します:= x。
ステップ2。ここで、角かっこから外します:x + x。
ステップ3。 角かっこを展開します:x + x + x + x。
ステップ4。 x + x +の符号を忘れずに、乗算します。
ステップ5。 式を単純化します。
同様に、絶対に任意の省略された乗算式を証明することができます。
FSOを使用した例とソリューション
原則として、これらの7つの式は、方程式や簡単な例を解くために式を単純化する必要がある場合に使用されます。
例1
タスク
式を簡略化します。
ご覧のとおり、最初の省略された乗算式であるSumSquareがこの例に適合します。
解決
最初の式に基づいて、例を因子に分解する必要があります。 これを行うには、数式を調べて、文字の代わりに数字を使用します。 この場合、「a」は3x、「b」は5です。
右側を考慮して結果を書き込みます。 我々が得る:
この例では、乗算されるすべてのものを乗算し、すぐに答えを得る必要があります。
もちろん、分数の例もあります。 しかし、簡単な例を解く方法を学べば、他のタイプを恐れることはありません。
例2
タスク
式を簡略化する
解決
= – x x + =
これらの式の二重積は、です。これは、三項式の2番目のメンバー(プラス記号付き)と一致します。これは、
したがって、ご覧のとおり、例では複雑なことは何もありません。 主なことは、数式、それらを適用できる場所、および数式なしで実行できる場所を知ることです。
有用な情報源
- Arefieva I. G.、Piryutko O. N. Algebra:一般中等教育機関の7年生向けの教科書マニュアル:ミンスク「NarodnayaAsveta」、2017年-304ページ。
- Nikolsky S. M.、Potapov M. K. Algebra Grade 7:M:2015-287p。
- Rubin A. G.、Chulkov P.V.代数。 中学1年生。 M:2015-224ページ
FSU-例を含むグレード7の代数の省略乗算の式更新日:2019年11月22日投稿者: 科学記事.Ru
レッスン内容2つの式の合計の2乗
多項式による多項式の乗算を大幅に簡略化できる場合がいくつかあります。 たとえば、そのような場合(2 バツ+ 3y) 2 .
式(2 バツ+ 3y)2は、それぞれが(2に等しい2つの多項式の乗算です。 バツ+ 3y)
(2バツ+ 3y) 2 = (2バツ+ 3y)(2バツ+ 3y)
多項式を多項式で乗算しました。 それを実行しましょう:
(2バツ+ 3y) 2 = (2バツ+ 3y)(2バツ+ 3y) = 4バツ 2 + 6xy + 6xy + 9y 2 = 4バツ 2 + 12xy+ 9y 2
つまり、式(2 バツ+ 3y)2は等しい 4バツ 2 + 12xy + 9y 2
(2バツ+ 3y) 2 = 4バツ 2 + 12xy+ 9y 2
より単純な同様の例を解いてみましょう。
(a + b) 2
表現 ( a + b)2は、2つの多項式の乗算であり、それぞれが( a + b)
(a + b) 2 = (a + b)(a + b)
この掛け算をしましょう:
(a + b) 2 = (a + b)(a + b) = a 2 + ab + ab + b 2 = a 2 + 2ab + b 2
それが表現です (a + b)2は等しい a 2 + 2ab + b 2
(a + b) 2 = a 2 + 2ab + b 2
ケース( a + b)2は任意に拡張できます aと b。 私たちが解決した最初の例、すなわち(2 バツ+ 3y)2はアイデンティティを使用して解決できます (a + b) 2 = a 2 + 2ab + b 2 。 これを行うには、変数の代わりに置換する必要があります aと b式からの対応する用語(2 バツ+ 3y)2。 この場合、変数 aマッチディック2 バツ、および変数 bマッチディック3 y
a = 2バツ
b = 3y
そして、アイデンティティを使用できます (a + b) 2 = a 2 + 2ab + b 2 、ただし変数の代わりに aと b式2を置き換える必要があります バツおよび3 yそれぞれ:
(2バツ+ 3y) 2 = (2バツ)2 + 2×2 バツ×3 y + (3y) 2 = 4バツ 2 + 12xy+ 9y 2
前回と同様に、多項式を取得しました 4バツ 2 + 12xy+ 9y 2 。 解決策は通常短く書かれており、心の中ですべての基本的な変換を実行します。
(2バツ+ 3y) 2 = 4バツ 2 + 12xy+ 9y 2
身元 (a + b) 2 = a 2 + 2ab + b 2 2つの式の合計の2乗の式と呼ばれます。 この式は次のように読み取ることができます。
2つの式の合計の二乗は、最初の式の二乗に最初の式と2番目の式の積の2倍を加えたものに、2番目の式の二乗を加えたものに等しくなります。
式(2 + 3)2を考えてみましょう。 これは、2つの方法で計算できます。角かっこで加算を実行して結果を二乗するか、2つの式の合計の二乗の式を使用します。
最初の方法:
(2 + 3) 2 = 5 2 = 25
2番目の方法:
(2 + 3)2 = 2 2 + 2×2×3 + 3 2 = 4 + 12 + 9 = 25
例2。 式を変換する(5 a+ 3)2を多項式に変換します。
2つの式の合計の2乗の式を使用してみましょう。
(a + b) 2 = a 2 + 2ab + b 2
(5+ 3) 2 = (5a)2 + 2×5 a× 3 + 3 2 = 25a 2 + 30a + 9
手段、 (5+ 3) 2 = 25a 2 + 30a + 9.
合計二乗式を使用せずに、この例を解いてみましょう。 同じ結果が得られるはずです。
(5+ 3) 2 = (5+ 3)(5+ 3) = 25a 2 + 15a + 15a + 9 = 25a 2 + 30a + 9
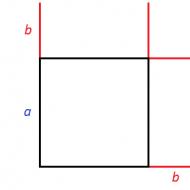
2つの式の合計の2乗の式には、幾何平均的な意味があります。 正方形の面積を計算するには、その辺を2乗する必要があることを覚えています。
たとえば、一辺のある正方形の面積 aに等しくなります a 2.2。 正方形の辺を大きくすると b、その場合、面積は( a + b) 2
次の図を検討してください。
この図に示されている正方形の辺が次のように増加していると想像してください。 b。 正方形はすべての辺が等しい。 その側が増加した場合 b、その後、反対側も増加します b

結果は、前の正方形よりも大きい新しい正方形になります。 それをよく見るために、欠けている側面を完成させましょう:

この正方形の面積を計算するには、それに含まれる正方形と長方形を別々に計算してから、結果を追加します。
まず、辺のある正方形を計算できます a-その面積はに等しくなります a 2.2。 次に、辺のある長方形を計算できます aと b-それらは等しくなります ab。 次に、辺のある正方形を計算できます b

結果は、次の面積の合計になります。
a 2 + ab + ab + b 2
同一の長方形の面積の合計は、2を掛けることで置き換えることができます ab、これは文字通り意味します 「長方形のabの領域を2回繰り返します」 。 代数的に、これは同類項を減らすことによって得られます abと ab。 結果は式です a 2 + 2ab+ b 2 、これは2つの式の合計の2乗の式の右辺です。
(a + b) 2 = a 2 + 2ab+ b 2
2つの式の差の2乗
2つの式の差の2乗の式は次のとおりです。
(a-b) 2 = a 2 − 2ab + b 2
2つの式の差の二乗は、最初の式の二乗から最初の式と2番目の式の積の2倍を引いたものに、2番目の式の二乗を加えたものに等しくなります。
2つの式の差の二乗の式は、2つの式の合計の二乗の式と同じ方法で導出されます。 表現 ( a-b)2は、2つの多項式の積であり、それぞれが( a-b)
(a-b) 2 = (a-b)(a-b)
この乗算を実行すると、多項式が得られます a 2 − 2ab + b 2
(a-b) 2 = (a-b)(a-b) = a 2 − ab− ab+ b 2 = a 2 − 2ab + b 2
例1。 式を変換する(7 バツ− 5)2を多項式に変換します。
2つの式の差の2乗の式を使用してみましょう。
(a-b) 2 = a 2 − 2ab + b 2
(7バツ− 5) 2 = (7バツ)2 −2×7 x× 5 + 5 2 = 49バツ 2 − 70バツ + 25
手段、 (7バツ− 5) 2 = 49バツ 2 + 70バツ + 25.
差分二乗式を使用せずに、この例を解いてみましょう。 同じ結果が得られるはずです。
(7バツ− 5) 2 = (7バツ− 5) (7バツ− 5) = 49バツ 2 − 35バツ − 35バツ + 25 = 49バツ 2 − 70バツ+ 25.
2つの式の差の2乗の式にも、幾何平均があります。 一辺のある正方形の面積の場合 aに等しい a 2、次に、辺が次のように縮小された正方形の面積 b、は(に等しくなります a-b) 2
次の図を検討してください。

この図に示されている正方形の辺が次のように縮小されていると想像してください。 b。 正方形はすべての辺が等しい。 片側が b、その後、反対側も減少します b

結果は、前の正方形よりも小さい新しい正方形になります。 図では黄色で強調表示されています。 その側は a− b古い側から aによって減少しました b。 この正方形の面積を計算するには、正方形の元の面積を使用できます a 2古い正方形の辺を減らす過程で得られた長方形の面積を引きます。 これらの長方形を表示してみましょう。

次に、次の式を記述できます。古い領域 a 2マイナスエリア abマイナス面積( a-b)b
a 2 − ab − (a-b)b
式の角かっこを展開します( a-b)b
a 2 − ab-ab + b 2
同様の用語は次のとおりです。
a 2 − 2ab + b 2
結果は式です a 2 − 2ab + b 2 、これは2つの式の差の2乗の式の右辺です。
(a-b) 2 = a 2 − 2ab + b 2
和の二乗と差の二乗の式は一般的に呼ばれます 省略された乗算式。 これらの式を使用すると、多項式の乗算プロセスを大幅に簡素化および高速化できます。
先ほど、多項式のメンバーを個別に検討する場合は、その前にある記号と一緒に検討する必要があると述べました。
ただし、省略された乗算式を適用する場合、元の多項式の符号をこの項自体の符号と見なすべきではありません。
たとえば、式(5 バツ − 2y)2、および式を使用したい (a-b) 2 = a 2 − 2ab + b 2 、その後の代わりに b 2を置き換える必要があります y、-2ではありません y。 これは、忘れてはならない数式を操作する機能です。
(5バツ − 2y) 2
a = 5バツ
b = 2y
(5バツ − 2y) 2 = (5バツ)2 −2×5 バツ×2 y + (2y) 2 = 25バツ 2 − 20xy + 4y 2
-2に置き換えると y、これは、元の式の角かっこ内の差が合計に置き換えられたことを意味します。
(5バツ − 2y) 2 = (5バツ + (−2y)) 2
この場合、差の2乗の式ではなく、合計の2乗の式を適用する必要があります。
(5バツ + (−2y) 2
a = 5バツ
b = −2y
(5バツ + (−2y)) 2 = (5バツ)2 + 2×5 バツ×(−2 y) + (−2y) 2 = 25バツ 2 − 20xy + 4y 2
例外は、フォームの式である可能性があります (バツ− (−y)) 2 。 この場合、式を使用します (a-b) 2 = a 2 − 2ab + b 2 それ以外の b置換する必要があります(- y)
(バツ− (−y)) 2 = バツ 2 −2× バツ× (− y) + (−y) 2 = バツ 2 + 2xy + y 2
しかし、フォームの表現を二乗する バツ − (−y)、減算を加算に置き換える方が便利です x + y。 次に、元の式は次の形式になります( x +y)2であり、差ではなく、合計の2乗の式を使用することが可能になります。
(x +y) 2 = バツ 2 + 2xy + y 2
合計キューブと差キューブ
2つの式の合計の立方体と2つの式の差の立方体の式は次のとおりです。
(a + b) 3 = a 3 + 3a 2 b + 3ab 2 + b 3
(a-b) 3 = a 3 − 3a 2 b + 3ab 2 − b 3
2つの式の合計の立方体の式は、次のように読み取ることができます。
2つの式の合計の立方体は、最初の式の立方体に最初の式の2乗の3倍に2番目の式を掛けたものに、最初の式の積に2番目の2乗を掛けたものに2番目の3乗を加えたものに等しくなります。表現。
そして、2つの式の差の立方体の式は次のように読み取ることができます。
2つの式の差の立方体は、最初の式の3乗から最初の式と2番目の式の積の3倍を引いたものに、最初の式と2番目の式の2乗の積から3倍を引いたものに等しくなります。 2番目の式の。
問題を解決するときは、これらの公式を心から知っておくことが望ましいです。 覚えていなくても心配しないでください! あなたは自分でそれらを取り出すことができます。 私たちはすでにその方法を知っています。
自分で合計キューブの式を導き出しましょう。
(a + b) 3
表現 ( a + b)3は、3つの多項式の積であり、それぞれが( a+ b)
(a + b) 3 = (a+ b)(a+ b)(a+ b)
しかし、表現( a + b)3は次のように書くこともできます (a+ b)(a+ b) 2
(a + b) 3 = (a+ b)(a+ b) 2
この場合、係数( a+ b)2は、2つの式の合計の2乗です。 合計のこの2乗は、式に等しくなります a 2 + 2ab + b 2 .
それで ( a + b)3は次のように書くことができます (a+ b)(a 2 + 2ab + b 2) .
(a + b) 3 = (a+ b)(a 2 + 2ab + b 2)
そして、これは多項式と多項式の乗算です。 それを実行しましょう:
(a + b) 3 = (a+ b)(a 2 + 2ab + b 2) = a 3 + 2a 2 b + ab 2 + a 2 b + 2ab 2 + b 3 = a 3 + 3a 2 b + 3ab 2 + b 3
同様に、2つの式の差の立方体の式を導き出すことができます。
(a-b) 3 = (a- b)(a 2 − 2ab + b 2) = a 3 − 2a 2 b + ab 2 − a 2 b + 2ab 2 − b 3 = a 3 − 3a 2 b+ 3ab 2 − b 3
例1。 式を変換します( バツ+ 1)3を多項式に変換します。
(a + b) 3 = a 3 + 3a 2 b + 3ab 2 + b 3
(バツ+ 1) 3 = バツ 3 + 3× バツ 2×1 + 3× バツ×12 + 1 3 = バツ 3 + 3バツ 2 + 3バツ + 1
2つの式の合計の3乗式を使用せずに、この例を解いてみましょう。
(バツ+ 1) 3 = (バツ+ 1)(バツ+ 1)(バツ+ 1) = (バツ+ 1)(バツ 2 + 2バツ + 1) = バツ 3 + 2バツ 2 + バツ + バツ 2 + 2バツ + 1 = バツ 3 + 3バツ 2 + 3バツ + 1
例2。 式を変換する (6a 2 + 3b 3) 3 多項式に。
2つの式の合計にキューブ式を使用してみましょう。
(a + b) 3 = a 3 + 3a 2 b + 3ab 2 + b 3
(6a 2 + 3b 3) 3 = (6a 2)3 + 3×(6 a 2)2×3 b 3 + 3×6 a 2 × (3b 3) 2 + (3b 3) 3 = 216a 6 + 3×36 a 4×3 b 3 + 3×6 a 2×9 b 6 + 27b 9
例3。 式を変換する( n 2 − 3)3を多項式に変換します。
(a-b) = a 3 − 3a 2 b + 3ab 2 − b 3
(n 2 − 3) 3 = (n 2)3 − 3×( n 2)2×3 + 3× n 2×32 − 3 3 = n 6 − 9n 4 + 27n 2 − 27
例4。 式を変換する (2バツ 2 − バツ 3) 3 多項式に。
2つの式の差の立方体式を使用してみましょう。
(a-b) = a 3 − 3a 2 b + 3ab 2 − b 3
(2バツ 2 − バツ 3) 3 = (2バツ 2)3 − 3×(2 バツ 2)2× バツ 3 + 3×2 バツ 2×( バツ 3) 2 − (バツ 3) 3 =
8バツ 6 −3×4 バツ 4× バツ 3 + 3×2 バツ 2× バツ 6 − バツ 9 =
8バツ 6 − 12バツ 7 + 6バツ 8 − バツ 9
2つの式の差にそれらの合計を掛ける
2つの式の差にそれらの合計を掛ける必要があるという問題があります。 例えば:
(a-b)(a + b)
この式では、2つの式の違い aと b同じ2つの式の合計を掛けます。 この掛け算をしましょう:
(a-b)(a + b) = a 2 + ab − ab − b 2 = a 2 − b 2
それが表現です (a-b)(a + b) 等しい a 2 − b 2
(a-b)(a + b) = a 2 − b 2
2つの式の差にそれらの合計を掛けると、これらの式の2乗の差が得られることがわかります。
2つの式の差とそれらの合計の積は、これらの式の2乗の差に等しくなります。
ハプニング (a-b)(a + b) 任意に拡張することができます aと b。 簡単に言えば、問題を解決するときに2つの式の差にそれらの合計を掛ける必要がある場合、この掛け算はこれらの式の2乗の差に置き換えることができます。
例1。 乗算を実行します (2バツ − 5)(2バツ + 5)
この例では、式の違いは2です。 バツ 5にこれらの同じ式の合計を掛けます。 次に、式に従って (a-b)(a + b) = a 2 − b 2 我々は持っています:
(2バツ − 5)(2バツ + 5) = (2バツ) 2 − 5 2
右側を計算すると、4が得られます バツ 2 − 25
(2バツ − 5)(2バツ + 5) = (2バツ) 2 − 5 2 = 4バツ 2 − 25
式を使用せずにこの例を解いてみましょう (a-b)(a + b) = a 2 − b 2 。 同じ結果が得られます4 バツ 2 − 25
(2バツ − 5)(2バツ + 5) = 4バツ 2 − 10バツ + 10バツ − 25 = 4バツ 2 − 25
例2。 乗算を実行します (4バツ − 5y)(4バツ + 5y)
(a-b)(a + b) = a 2 − b 2
(4バツ − 5y)(4バツ + 5y) = (4バツ) 2 − (5y) 2 = 16バツ 2 − 25y 2
例3。 乗算を実行します (2a+ 3b)(2a− 3b)
2つの式の差にそれらの合計を掛ける式を使用してみましょう。
(a-b)(a + b) = a 2 − b 2
(2+ 3b)(2a- 3b) = (2a) 2 − (3b) 2 = 4a 2 − 9b 2
この例では、項の合計は2です。 aおよび3 bこれらの用語の違いよりも前にあります。 そして式の中で (a-b)(a + b) = a 2 − b 2 違いは先にあります。
ファクターの配置方法に違いはありません( a-b) の ( a + b)式で。 それらは次のように書くことができます (a-b)(a + b) 、 と (a + b)(a-b) 。 結果はまだ a 2 − b 2、積は因子の順列から変化しないため。
したがって、この例では、要因(2 + 3b)および2 a- 3b)は次のように書くことができます (2+ 3b)(2a- 3b) 、 と (2a- 3b)(2+ 3b) 。 結果はまだ4になります。 a 2 − 9b 2 .
例3。 乗算を実行します (7 + 3バツ)(3バツ − 7)
2つの式の差にそれらの合計を掛ける式を使用してみましょう。
(a-b)(a + b) = a 2 − b 2
(7 + 3バツ)(3バツ − 7) = (3バツ) 2 − 7 2 = 9バツ 2 − 49
例4。 乗算を実行します (バツ 2 − y 3)(バツ 2 + y 3)
(a-b)(a + b) = a 2 − b 2
(バツ 2 − y 3)(バツ 2 + y 3) = (バツ 2) 2 − (y 3) 2 = バツ 4 − y 6
例5。 乗算を実行します (−5バツ− 3y)(5バツ− 3y)
式(-5 バツ− 3y)-1を取り出すと、元の式は次の形式になります。
(−5バツ− 3y)(5バツ− 3y) = −1(5バツ + 3y)(5バツ − 3y)
仕事 (5バツ + 3y)(5バツ − 3y) 二乗の差で置き換えます:
(−5バツ− 3y)(5バツ− 3y) = −1(5バツ + 3y)(5バツ − 3y) = −1((5バツ) 2 − (3y) 2)
二乗の差は括弧で囲まれています。 これを行わないと、-1に(5)だけが掛けられることがわかります。 バツ)2。 そして、これはエラーにつながり、元の式の値を変更します。
(−5バツ− 3y)(5バツ− 3y) = −1(5バツ + 3y)(5バツ − 3y) = −1((5バツ) 2 − (3y) 2) = −1(25バツ 2 − 9バツ 2)
ここで、-1に括弧で囲まれた式を掛けて、最終結果を取得します。
(−5バツ− 3y)(5バツ− 3y) = −1(5バツ + 3y)(5バツ − 3y) = −1((5バツ) 2 − (3y) 2) =
−1(25バツ 2 − 9y 2) = −25バツ 2 + 9y 2
2つの式の差に、それらの合計の不完全な2乗を掛けます
2つの式の差にそれらの合計の不完全な2乗を掛ける必要があるという問題があります。 この作品は次のようになります。
(a-b)(a 2 + ab + b 2)
最初の多項式( a-b)は、2つの式の差であり、2番目の多項式です。 (a 2 + ab + b 2) これら2つの式の合計の不完全な二乗です。
合計の不完全な二乗は、次の形式の多項式です。 a 2 + ab + b 2 。 合計の通常の二乗に似ています a 2 + 2ab + b 2
たとえば、式 4バツ 2 + 6xy + 9y 2 式2の合計の不完全な二乗です バツおよび3 y .
確かに、式の最初の用語 4バツ 2 + 6xy + 9y 2 、すなわち4 バツ 2は式2の2乗です バツ、(2 バツ) 2 = 4バツ 2.2。 式の第3項 4バツ 2 + 6xy + 9y 2 、すなわち9 y 2は3の平方根です y、(3 y) 2 = 9y 2.2。 ミッドディック6 xy、は式2の積です バツおよび3 y。
それでは、差を掛けましょう( a-b)合計の不完全な二乗による a 2 + ab + b 2
(a-b)(a 2 + ab + b 2) = a(a 2 + ab + b 2) − b(a 2 + ab + b 2) =
a 3 + a 2 b + ab 2 − a 2 b − ab 2 − b 3 = a 3 − b 3
それが表現です (a-b)(a 2 + ab + b 2) 等しい a 3 − b 3
(a-b)(a 2 + ab + b 2) = a 3 − b 3
このアイデンティティは、2つの式の差にそれらの合計の不完全な2乗を掛けるための式と呼ばれます。 この式は次のように読み取ることができます。
2つの式の差とそれらの合計の不完全な二乗の積は、これらの式の3乗の差に等しくなります。
例1。 乗算を実行します (2バツ − 3y)(4バツ 2 + 6xy + 9y 2)
最初の多項式(2 バツ − 3y)は2つの式の違いです2 バツおよび3 y。 2番目の多項式 4バツ 2 + 6xy + 9y 2 2つの式の合計の不完全な二乗です2 バツおよび3 y。 これにより、時間のかかる計算を行わずに数式を使用できます (a-b)(a 2 + ab + b 2) = a 3 − b 3 。 私たちの場合、乗算 (2バツ − 3y)(4バツ 2 + 6xy + 9y 2) 立方体の違いで置き換えることができます2 バツおよび3 y
(2バツ − 3y)(4バツ 2 + 6xy + 9y 2) = (2バツ) 3 − (3y) 3 = 8バツ 3 − 27y 3
(a-b)(a 2 + ab+ b 2) = a 3 − b 3 。 同じ結果が得られますが、解決策は長くなります。
(2バツ − 3y)(4バツ 2 + 6xy + 9y 2) = 2バツ(4バツ 2 + 6xy + 9y 2) − 3y(4バツ 2 + 6xy + 9y 2) =
8x 3 + 12バツ 2 y + 18xy 2 − 12バツ 2 y − 18xy 2 − 27y 3 = 8バツ 3 − 27y 3
例2。 乗算を実行します (3 − バツ)(9 + 3バツ + バツ 2)
最初の多項式(3 − バツ)は2つの式の差であり、2番目の多項式はこれら2つの式の合計の不完全な2乗です。 これにより、式を使用できます (a-b)(a 2 + ab + b 2) = a 3 − b 3
(3 − バツ)(9 + 3バツ + バツ 2) = 3 3 − バツ 3 = 27 − バツ 3
2つの式の合計に、それらの差の不完全な2乗を掛けます
2つの式の合計にそれらの差の不完全な2乗を掛ける必要があるという問題があります。 この作品は次のようになります。
(a + b)(a 2 − ab + b 2)
最初の多項式( a + b (a 2 − ab + b 2) は、これら2つの式の差の不完全な二乗です。
差の不完全な二乗は、次の形式の多項式です。 a 2 − ab + b 2 。 通常の二乗の差に似ています a 2 − 2ab + b 2 ただし、最初の式と2番目の式の積が2倍にならない点が異なります。
たとえば、式 4バツ 2 − 6xy + 9y 2 式2の違いの不完全な二乗です バツおよび3 y。
(2バツ) 2 − 2バツ×3 y + (3y) 2 = 4バツ 2 − 6xy + 9y 2
元の例に戻りましょう。 合計を掛けましょう a + b差の不完全な二乗によって a 2 − ab + b 2
(a + b)(a 2 − ab + b 2) = a(a 2 − ab + b 2) + b(a 2 − ab + b 2) =
a 3 − a 2 b + ab 2 + a 2 b − ab 2 + b 3 = a 3 + b 3
それが表現です (a + b)(a 2 − ab + b 2) 等しい a 3 + b 3
(a + b)(a 2 − ab + b 2) = a 3 + b 3
このアイデンティティは、2つの式の合計にそれらの差の不完全な2乗を掛けるための式と呼ばれます。 この式は次のように読み取ることができます。
2つの式の合計とそれらの差の不完全な二乗の積は、これらの式の3乗の合計に等しくなります。
例1。 乗算を実行します (2バツ + 3y)(4バツ 2 − 6xy + 9y 2)
最初の多項式(2 バツ + 3y)は2つの式の合計です2 バツおよび3 y、および2番目の多項式 4バツ 2 − 6xy + 9y 2 これらの式の差の不完全な二乗です。 これにより、時間のかかる計算を行わずに数式を使用できます (a + b)(a 2 − ab + b 2) = a 3 + b 3 。 私たちの場合、乗算 (2バツ + 3y)(4バツ 2 − 6xy + 9y 2) 立方体2の合計で置き換えることができます バツおよび3 y
(2バツ + 3y)(4バツ 2 − 6xy + 9y 2) = (2バツ) 3 + (3y) 3 = 8バツ 3 + 27y 3
式を使用せずに同じ例を解いてみましょう (a + b)(a 2 − ab+ b 2) = a 3 + b 3 。 同じ結果が得られますが、解決策は長くなります。
(2バツ + 3y)(4バツ 2 − 6xy + 9y 2) = 2バツ(4バツ 2 − 6xy + 9y 2) + 3y(4バツ 2 − 6xy + 9y 2) =
8バツ 3 − 12バツ 2 y + 18xy 2 + 12バツ 2 y − 18xy 2 + 27y 3 = 8バツ 3 + 27y 3
例2。 乗算を実行します (2バツ+ y)(4バツ 2 − 2xy + y 2)
最初の多項式(2 バツ+ y)は、2つの式の合計であり、2番目の多項式です。 (4バツ 2 − 2xy + y 2) これらの式の違いの不完全な二乗です。 これにより、式を使用できます (a + b)(a 2 − ab+ b 2) = a 3 + b 3
(2バツ+ y)(4バツ 2 − 2xy + y 2) = (2バツ) 3 + y 3 = 8バツ 3 + y 3
式を使用せずに同じ例を解いてみましょう (a + b)(a 2 − ab+ b 2) = a 3 + b 3 。 同じ結果が得られますが、解決策は長くなります。
(2バツ+ y)(4バツ 2 − 2xy + y 2) = 2バツ(4バツ 2 − 2xy + y 2) + y(4バツ 2 − 2xy + y 2) =
8バツ 3 − 4バツ 2 y + 2xy 2 + 4バツ 2 y − 2xy 2 + y 3 = 8バツ 3 + y 3
独立したソリューションのタスク
レッスンは気に入りましたか?
新しいVkontakteグループに参加して、新しいレッスンの通知を受け取り始めます
>>数学:乗算式の削減
省略された乗算式
ある多項式を別の多項式で乗算すると、コンパクトで覚えやすい結果が得られる場合がいくつかあります。 このような場合、毎回1回乗算しないことが望ましいです。 多項式一方、完成した結果を使用します。 これらのケースを考えてみましょう。
1.合計の2乗と差の2乗:
例1式の角かっこを開きます。
a)(3x + 2)2;
b)(5a 2--4b 3)2
a)式(1)を使用します。 aの役割は3倍であり、bの役割は2番であることを考慮に入れます。
我々が得る:
(Zx + 2)2 =(3x)2 + 2 Zx 2 + 2 2 = 9x 2 + 12x +4。
b)式(2)を使用します、役割でそれを考慮して しかし話す 5a 2、および役割で b話す 4b 3。 我々が得る:
(5a 2 -4b 3)2 \ u003d(5a 2)2 --2-5a 2 4b 3 +(4b 3)2 \ u003d 25a 4 -40a 2 b 3 + 16b6。
合計の2乗または差の2乗の式を使用する場合は、次の点に注意してください。
(-a --b)2 \ u003d(a + b)2;
(b-a)2 =(a-b)2。
これは、(-a)2 = a2であるという事実に基づいています。
いくつかの数学的トリックは式(1)と(2)に基づいており、頭の中で計算を行うことができることに注意してください。
たとえば、1と9で終わる数字を実際に口頭で二乗することができます。
71 2 = (70 + 1) 2 = 70 2 + 2 70 1 + 1 2 = 4900 + 140 + 1 = 5041;
91 2 =(90 + I)2 = 90 2 + 2 90 1 + 1 2 = 8100 + 180 + 1 = 8281;
69 2 \ u003d(70-I)2 \ u003d 70 2-2 70 1 + 1 2 \ u003d 4900-140 + 1 \ u003d4761。
2または8で終わる数をすばやく二乗することもできます。たとえば、
102 2 = (100 + 2) 2 = 100 2 + 2 100 2 + 2 2 = 10 000 + 400 + 4 = 10 404;
48 2 = (50 - 2) 2 = 50 2 - 2 50 2 + 2 2 = 2500 - 200 + 4 = 2304.
しかし、最もエレガントなトリックは、5で終わる数字を二乗することです。
852の対応する推論を実行してみましょう。
我々は持っています:
85 2 = (80 + 5) 2 = 80 2 + 2 80 5 + 5 2 =-80 (80+ 10)+ 25 = 80 90 + 25 = 7200 + 25 = 7225.
85 2を計算するには、8に9を掛けて、得られた結果の右側に25を加えるだけで十分であることに注意してください。同様に、他の場合にも同じことができます。 たとえば、35 2 \ u003d 1225(3 4 \ u003d 12と25が右側の結果の数値に追加されました)。
65 2 = 4225; 1252 \ u003d 15625(12 18 \ u003d 156および25が、右側の結果の数値に追加されました)。
退屈な(一見)式(1)と(2)に関連するさまざまな奇妙な状況について話しているので、この会話を次の幾何学的な推論で補足します。 aとbを正の数とします。 辺がa + bの正方形を考え、その2つの角で辺がそれぞれaとbに等しい正方形を切り取ります(図4)。

辺がa + bの正方形の面積は(a + b)2です。 しかし、この正方形を4つの部分に分割します:辺がaの正方形(その面積は2)、辺がbの正方形(その面積はb 2)、辺がaとbの2つの長方形(それぞれの面積)長方形はab)です。 したがって、(a + b)2 = a 2 + b 2 + 2ab、つまり、式(1)が得られます。
二項式a + bに二項式a--bを掛けます。 我々が得る:
(a + b)(a --b)\ u003d a 2-ab + ba --b 2 \ u003d a 2-b2。
それで
数学の等式は、左から右(つまり、等式の左側が右側に置き換えられる)と右から左(つまり、等式の右側が左側に置き換えられる)の両方で使用されます。 式C)を左から右に使用すると、積(a + b)(a --b)を最終結果a 2 --b2に置き換えることができます。 同じ式を右から左に使用できます。これにより、二乗の差a 2 --b 2を積(a + b)(a --b)に置き換えることができます。 数学の式(3)には、二乗の差という特別な名前が付けられています。
コメント。
「二乗の差」と「二乗の差」という用語を混同しないでください。 二乗の差は2-b 2です。これは、式(3)について話していることを意味します。 差の二乗は(a-b)2なので、式(2)について話します。 通常の言語では、式(3)は「右から左へ」次のように読み取られます。
2つの数値(式)の二乗の差は、これらの数値(式)の合計とそれらの差の積に等しくなります。
例2乗算を実行します
(3x-2y)(3x + 2y)
解決。 我々は持っています:
(3x-2y)(3x + 2y)\ u003d(3x)2-(2y)2 \ u003d 9x 2-4y2。
例3二項式の積として二項式16x4-9を表現します。
解決。 16x 4 \ u003d(4x 2)2、9 \ u003d Z 2があります。これは、与えられた二項式が二乗の差であることを意味します。 右から左に読む式(3)を適用できます。 次に、次のようになります。
16x 4-9 =(4x 2)2-W 2 =(4x 2 + 3)(4x 2-3)
式(3)は、式(1)および(2)と同様に、数学的なトリックに使用されます。 見る:
79 81 =(80-1)(80 + 1)-802-I2 = 6400-1 = 6399;
42 38 = D0 + 2)D0-2)= 402-22 = 1600-4 = 1596。
奇妙な幾何学的な推論で二乗の差の公式についての会話を終えましょう。 aとbを正の数とします。ここで、a> bです。 辺がa + bとa--bの長方形を考えてみましょう(図5)。 その面積は(a + b)(a --b)です。 図6に示すように、辺がbとa --bの長方形を切り取り、残りの部分に接着します。結果の図が同じ面積、つまり(a + b)(a --b)を持っていることは明らかです。 しかし、この数字は
次のように作成します。辺aの正方形から、辺bの正方形を切り取ります(これは図6にはっきりと示されています)。 したがって、新しい図の面積は2 --b2です。 したがって、(a + b)(a --b)\ u003d a 2 --b 2、つまり、式(3)が得られます。

3.立方体の違いと立方体の合計
二項式a--bに三項式a2 + ab + b2を掛けます。
我々が得る:
(a --b)(a 2 + ab + b 2)\ u003d a a 2 + a ab + a b 2 --b a 2 --b ab -bb 2 \ u003d a 3 + a 2 b + ab 2 -a 2 b- ab 2 -b 3 \ u003d a 3 -b3。
同様に
(a + b)(a 2-ab + b 2)= a 3 + b 3
(自分で確認してください)。 それで、

式(4)は通常呼ばれます 立方体の違い、式(5)-立方体の合計。 式(4)と(5)を通常の言語に翻訳してみましょう。 これを行う前に、式a 2 + ab + b 2は、式(1)に表示され、(a + b)2を与える式a 2 + 2ab + b2に類似していることに注意してください。 式a2-ab + b 2は、式(2)に現れて(a-b)2を与える式a 2-2ab + b2に似ています。
これらの式のペアを(言語で)区別するために、各式a 2 + 2ab + b2およびa2-2ab + b 2は完全な二乗(合計または差)と呼ばれ、各式はa 2 + ab + b2およびa2-ab + b 2は、不完全な二乗(合計または差)と呼ばれます。 次に、式(4)と(5)(「右から左へ」と読みます)を通常の言語に翻訳します。
2つの数値(式)の立方体の差は、これらの数値(式)の差とそれらの合計の不完全な2乗の積に等しくなります。 2つの数値(式)の3乗の合計は、これらの数値(式)の合計とそれらの差の不完全な2乗の積に等しくなります。
コメント。 このセクションで得られたすべての式(1)〜(5)は、左から右と右から左の両方で使用されます。最初の場合(左から右)にのみ、(1)〜(5)は乗算の省略形であると言われます。式、および2番目のケース(右から左へ)では、(1)-(5)は因数分解式であると言います。
例4(2x-1)(4x2 + 2x + 1)を掛けます。
解決。 最初の要因は単項式2xと1の差であり、2番目の要因はそれらの合計の不完全な二乗であるため、式(4)を使用できます。 我々が得る:
(2x-1)(4x 2 + 2x + 1)\ u003d(2x)3-I 3 \ u003d 8x3-1。
例5二項式27a6 + 8b3を多項式の積として表現します。
解決。 27а6=(2の場合)3、8b 3 =(2b)3。 これは、与えられた二項式が立方体の合計であることを意味します。つまり、式95)を適用して、右から左に読み取ることができます。 次に、次のようになります。
27a 6 + 8b 3 =(2の場合)3 +(2b)3 =(2 + 2bの場合)((2の場合)2-2の場合2b +(2b)2)=(2 + 2bの場合)(9a 4- 6a 2 b + 4b 2)。
オンラインで生徒を支援する、7年生向けの数学のダウンロード、カレンダーをテーマにした計画
A. V. Pogorelov、7〜11年生の幾何学、教育機関向けの教科書
レッスン内容 レッスンのまとめサポートフレームレッスンプレゼンテーション加速方法インタラクティブテクノロジー 練習 タスクと演習自己診断ワークショップ、トレーニング、ケース、クエスト宿題ディスカッション質問学生からの修辞的な質問 イラスト オーディオ、ビデオクリップ、マルチメディア写真、写真、グラフィック、表、スキームのユーモア、逸話、ジョーク、漫画の寓話、ことわざ、クロスワードパズル、引用 アドオン アブストラクト好奇心旺盛なチートシートの教科書の基本的な用語集とその他の用語の追加の用語集のための記事チップ 教科書とレッスンの改善教科書の誤りを訂正するレッスンの革新の教科書要素の断片を更新して、古い知識を新しい知識に置き換えます 教師のみ 完璧なレッスンディスカッションプログラムの年間方法論的推奨事項のカレンダー計画 統合されたレッスン