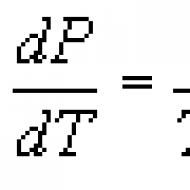Clapeyron-Clausiusova jednadžba. Clapeyron i Clausius-Clapeyron jednadžbe Za koje fazne prijelaze je Clapeyron jednadžba primjenjiva?
Clapeyron-Clausiusova jednadžba termodinamička jednačina koja se odnosi na procese prelaska supstance iz jedne faze u drugu (isparavanje, topljenje, sublimacija, polimorfna transformacija, itd.). Prema K. - K. u., toplota faznog prijelaza (na primjer, toplota isparavanja, toplota fuzije) tokom ravnotežnog procesa određena je izrazom Gdje T - prelazna temperatura (izotermni proces), dp/dT - vrijednost derivata pritiska u odnosu na temperaturu na datoj prijelaznoj temperaturi, ( V 2 -V 1) - promjena zapremine supstance tokom njenog prelaska iz prve faze u drugu. Jednačinu je prvobitno dobio 1834. B. P. E. Clapeyron analizom Carnotovog ciklusa za kondenzaciju pare u termalnoj ravnoteži s tekućinom. 1850. P. Clausius je poboljšao jednačinu i proširio je na druge fazne prelaze. K. - K. u. primjenjiv na bilo koje fazne prijelaze praćene apsorpcijom ili oslobađanjem topline (tzv. fazni prijelaz prvog reda), a direktna je posljedica uslova fazne ravnoteže (vidi Fazna ravnoteža) ,
iz koje je izvedeno. K. - K. u. može se koristiti za izračunavanje bilo koje veličine uključene u jednadžbu, ako su ostale poznate. Konkretno, koristi se za izračunavanje topline isparavanja, čije je eksperimentalno određivanje ispunjeno značajnim poteškoćama. Često K. - K. u. napisano u odnosu na derivate dp/dT ili dT/dp:
Za procese isparavanja i sublimacije dp/dT izražava promjenu pritiska zasićene pare R sa temperaturom T, i za procese topljenja i polimorfne transformacije dT/dp određuje promjenu temperature prijelaza s pritiskom. Drugim riječima, K. - K. u. je diferencijalna jednadžba krivulje fazne ravnoteže u varijablama r, T.
Za rješavanje K. - K. u. potrebno je znati kako se količine mijenjaju s temperaturom i pritiskom L, V 1 I V 2,što je težak zadatak. Obično ovu zavisnost utvrđuje empirijski i rješava K. - K. u. brojčano. K. - K. u. primjenjiv i na čiste tvari i na otopine i pojedinačne komponente otopina. U potonjem slučaju, K. - K. u. povezuje parcijalni pritisak zasićene pare date komponente sa njenom parcijalnom toplotom isparavanja. Yu. I. Polyakov. Velika sovjetska enciklopedija. - M.: Sovjetska enciklopedija.
1969-1978
.
![]()
Pogledajte šta je "Clapeyron-Clausiusova jednačina" u drugim rječnicima:
CLAPEYRON MENDELEEVOVA JEDNAČINA, jednačina stanja (vidi JEDNAČINA STANJA) za idealni gas (vidi IDEALNI GAS), odnosi se na 1 mol (vidi MOL) gasa. Godine 1874. D.I. Mendeljejev (vidi MENDELEEV Dmitrij Ivanovič) na osnovu Clapeyronove jednadžbe ... ... enciklopedijski rječnik
CLAPEYRON-CLAUSIS JEDNAČINA- termodinamička jednačina koja se odnosi na procese prelaska supstance iz jedne faze u drugu (isparavanje, topljenje, polimorfna transformacija, itd.). Prema Clapeyron Clausis jednadžbi, toplina faznog prijelaza (na primjer, toplina topljenja ... Metalurški rječnik
Jednačina stanja idealnog gasa, uspostavljanje veze između njegove zapremine V. pritisak pi abs. t roy T. Ima oblik: pV=nRT. gdje je n broj molova plina, R = 8,31431 J/mol. K) gasna konstanta. Za 1 mol gasa pv=RT, gde je v molarni volumen. K.M.u....... Hemijska enciklopedija
Jednačina stanja Ovaj članak je dio serije Termodinamika. Jednačina stanja idealnog gasa Van der Waalsova jednačina Ditericijeva jednačina Sekcije termodinamike Principi termodinamike Jednačina ... Wikipedia
- (Clapeyron-Mendeleev jednačina), odnos između parametara idealnog gasa (pritisak p, zapremina V i apsolutna temperatura T), koji određuju njegovo stanje: pV=BT, gde je koeficijent. proporcionalnost B zavisi od mase gasa M i njegovog mola. mase. Instalirano… … Fizička enciklopedija
Jednadžba stanja Stat ... Wikipedia
- (Clapeyron-Mendeleev jednadžba), odnos između pritiska p, apsolutne temperature T i zapremine V idealnog gasa mase M: pV=BT, gde je B=M/m (m je masa molekula gasa u atomskoj masi jedinice). Osnovao francuski naučnik B.P.E. Clapeyron ... ... Moderna enciklopedija- Clapeyron Mendelejev jednadžba, koju je pronašao B. P. E. Clapeyron (1834) odnos između fizičkih veličina koje određuju stanje idealnog plina: tlak plina p, njegov volumen V i apsolutna temperatura T. K. u.... ... Velika sovjetska enciklopedija
Clapeyron Mendeleev jednadžba [nazvana po Francuzima. fizike B. Clapeyrona (V. Clapeyron; 1799 1864) i ruskog. hemičar D.I. Mendeljejev (1834 1907)], nivo stanja idealnog gasa: pVm = RT, gde je p pritisak, T je termodinamička temperatura gasa, Vm ... ... Veliki enciklopedijski politehnički rječnik
CLAPEYRON I CLAUSIUS-CLAPEYRON JEDNAČINE
Kao što slijedi iz Gibbsovog faznog pravila, broj nezavisnih intenzivnih varijabli u dvofaznom jednokomponentnom sistemu jednak je jedan. Stoga mora postojati jednačina koja se odnosi R I TV takav sistem. Ovaj odnos je posledica uslova fazne ravnoteže:
gdje je oznaka p(p, T) naglašava da je hemijski potencijal svake faze funkcija rT.
Ako je zavisnost p od R I T bila eksplicitno poznata, onda (3.7) bi se u principu moglo riješiti u odnosu na R ili T i pronađite zavisnost R = p(T) ili T = T(r). Međutim, u opštem slučaju, zavisnost p negativan i 7" nije poznato i to se ne može učiniti. Ali možete pronaći izvod R By T(ili njegov inverz).
Pretpostavimo da su dvije faze a i b jedne supstance u ravnoteži. Ako promenite temperaturu za vrednost d7", tada bi se pritisak trebalo promeniti tako da se hemijski potencijali obe faze menjaju podjednako, bez narušavanja uslova ravnoteže (3.7), tj.
Dekomponovanje oba diferencijala u varijable Tyr, dobijamo
Zajedno sa relacijama (2.31) ovo daje:
Iz ovoga proizlazi:
gdje je Df P? - entropija faznog prelaza; A fp U=U^ -- kutnjak
volumen faznog prijelaza (promjena molarne zapremine sa T= const, p = const).
Entropija i entalpija faznog prelaza su međusobno povezane relacijom (3.5): AS = AN/T. Stoga se (3.9) može napisati u sljedećem obliku: 
Gdje T- temperatura faznog prijelaza.
Jednačine (3.9) i (3.10) su ekvivalentne i svaka od njih se naziva Clapeyronova jednačina.
Praktična primjena Clapeyronove jednadžbe ograničena je činjenicom da entalpija faznog prijelaza i molarni volumeni faza različito zavise od temperature za različite faze. To znači da ne postoji opšti način da se ova jednačina integriše. Ali za male temperaturne intervale ove jednačine se mogu integrisati sa tačnošću dovoljnom za mnoge svrhe prihvatanjem određenih aproksimacija.
Prva aproksimacija je da se za uski temperaturni raspon može pretpostaviti da je entalpija faznog prijelaza približno konstantna. Isto se može učiniti i s obzirom na molarne zapremine kondenzovanih faza - čvrste i tečne, jer one slabo zavise od Tyr. Zatim, za fazne ravnoteže između čvrstih faza i između čvrste i tečne faze, promena molarne zapremine se takođe može pretpostaviti konstantnom. Sa ovim aproksimacijama (3.10) se integriše na sledeći način (za topljenje):

Slično za ravnoteže između čvrstih faza.
Molarni volumen gasne faze ne može se smatrati konstantnim. Ali za slučaj niskih pritisaka moguće su i druge aproksimacije. Prvo, molarni volumen gasa pri niskim pritiscima je mnogo veći od molarne zapremine bilo koje kondenzovane faze (cf). Stoga, za isparavanje možete uzeti:
Drugo, pri niskim pritiscima mnogi gasovi imaju
tt t^gas CT d__ Yat
svojstva blizu idealne. Stoga ~-i L isp k t ~-.
Zamijenivši ovo u jednačinu (3.10), dobijamo:

Jer &r/r= s!1p R, rezultirajući odnos naziva se Clausius-Clapeyronova jednačina:
Primjenjivo je za isparavanje tekućih i čvrstih faza (sublimacija).
U aproksimaciji konstantne entalpije faznog prijelaza, ova jednačina je integrirana na sljedeći način:
Za primjenu ovih jednadžbi često se koriste podaci o entalpijama faznih prijelaza i temperaturama faznih prijelaza pri normalnom tlaku. One su date u mnogim referentnim knjigama fizičkih i hemijskih veličina. Normalan pritisak je vrednost 101,325 Pa = 101,325 kPa = 1,01325 bar = 1 atm = 760 mm Hg. Art. = 760 Torr. Podaci iz priručnika služe kao osnova za približne proračune pomoću jednačina (3.11) i (3.13) pri pritiscima koji se značajno ne razlikuju od normalnih.
Molarne zapremine kondenzovanih faza potrebne za proračune pomoću jednačine (3.11) obično se ne navode u referentnim knjigama. Ali umjesto njih možete pronaći podatke o gustoći rijeka. Mogu se koristiti za izračunavanje molarnih volumena, znajući definicije U t = U/n, p = to I M = t/p. Od njih slijedi: U t = M/ p, gdje M - molarna masa.
S druge strane, neke referentne knjige daju specifične toplote faznih prelaza. Za ovaj slučaj, jednačina (3.10) se može napisati u sljedećem obliku:

gdje su Af p/g i Af P y promjene specifične entalpije i specifičnog volumena, respektivno, tokom faznog prijelaza (i v= 1/r).
Ako entalpija isparavanja nije poznata, ponekad se može približno procijeniti koristeći Troutonovo pravilo, koje kaže da je molarna entropija isparavanja većine tekućina približno 90 J K -1 mol -1 . Pošto je Dfp^ - AfpR/G, L isp R/J mol -1 = 90(G M/K), gdje je 7^ tačka ključanja pri normalnom pritisku. Zamjenjujući ovu vrijednost entalpije isparavanja u (3.13) i uzimajući za p x normalan pritisak je 1 atm, a za temperaturu T! normalna tačka ključanja T dobijamo za ravnotežni pritisak pare iznad tečnosti:

Troutonovo pravilo se ne odnosi na tečnosti visokog polariteta, a posebno na povezane tečnosti kao što su voda i alkoholi. (Povezane tekućine su tekućine čiji molekuli međusobno djeluju vodonične veze.) Pravilo je zadovoljavajuće samo kada se primjenjuje na nepolarne tvari i s tačkom ključanja u rasponu od približno 150 do 1000 K.
Clapeyron-Clausiusova jednadžba (diferencijalna).
Pročitajte također:
|
Krivulja ravnoteže tekućina-para ili, što je isto, ovisnost tlaka zasićene pare od temperature za datu supstancu može se naći rješavanjem takozvane Clapeyron-Clausiusove jednačine.
Metoda termodinamičkih ciklusa nam omogućava da ustanovimo oblik ove jednačine. Neka postoje dvije eksperimentalne izoterme, koje odgovaraju temperaturama i (slika 50).

U početnom stanju 1, jedan mol tečnosti je pod pritiskom na temperaturi i zauzima zapreminu (nema parne faze). Dodavanjem toplote izotermički isparavamo ovaj mol tečnosti. U ovom slučaju, tečnost će uvek biti pod pritiskom jednak pritisku njene zasićene pare. Kao rezultat, tečnost će se pretvoriti u gasovito stanje 2. Količina toplote potrebna da se jedan mol tečnosti pretvori u gasovito stanje pri konstantnoj temperaturi i pritisku je, po definiciji, latentna toplota isparavanja. Dakle, na prelazu 12 tečnost je primila količinu toplote jednaku .
Rad po ciklusu je numerički jednak površini četverokuta 1234:
![]() (3.3.1)
(3.3.1)
i efikasnost ciklusa
 .
(3.3.2)
.
(3.3.2)
S druge strane, ciklus 1234 je Carnotov ciklus, pa je njegova efikasnost
![]() (3.3.3)
(3.3.3)
Upoređujući izraze (3.3.2) i (3.3.3), dobijamo

 .
(3.3.4)
.
(3.3.4)
Jednačina (3.3.4) se može predstaviti u nešto drugačijem obliku. Da bismo to uradili, naći ćemo promenu entropije tokom prelaska tečnosti iz stanja 1 u gasovito stanje 2 (slika 50).
 ,
(3.3.5)
,
(3.3.5)
gdje su i entropije tekućine u stanju 1 i pare u stanju 2, respektivno. Koristeći posljednju relaciju, jednačina (3.3.4) se može napisati na sljedeći način:
 .
(3.3.6)
.
(3.3.6)
Diferencijalna jednačina (3.3.4) je Clapeyron–Clausiusova jednačina. Ova jednadžba predstavlja promjenu tlaka zasićene pare kako se temperatura mijenja za . Za pronalaženje rješenja ove jednačine potrebno je poznavati ovisnost latentne topline isparavanja o temperaturi, kao i ovisnost volumena tekućine i plina o temperaturi i tlaku. U opštem slučaju, ova jednadžba je nelinearna diferencijalna jednadžba čije se rješenje pronalazi numeričkom integracijom.
Na temperaturama znatno nižim od kritične, zapremina koju zauzima tečnost je mnogo manja od zapremine koju zauzima tečnost, tj. Tako je, na primjer, volumen vodene pare 1600 puta veći od volumena vode, ključanje tekućeg kisika na temperaturi od – C praćeno je povećanjem volumena za otprilike 300 puta. Stoga će na temperaturama jednačina (3.3.4) poprimiti oblik
. (3.3.7)
U istoj aproksimaciji, zasićena para se takođe može smatrati idealnim gasom. Ovo nam omogućava da zapišemo jednačinu (3.3.7) kao:
. (3.3.8)
Integracijom lijeve strane jednačine (3.3.8) u rasponu od do , a desne strane – u rasponu od do , dobijamo
 ,
(3.3.9)
,
(3.3.9)
gdje je tlak zasićene pare dobiven eksperimentom na temperaturi, i srednja vrijednost topline isparavanja u temperaturnom rasponu
Iz formule (3.3.9) je jasno da pritisak zasićenih para raste eksponencijalno sa porastom temperature.
Clapeyron–Clausiusova jednačina prepisana kao
 , (3.3.10)
, (3.3.10)
kao što ćemo kasnije pokazati, on takođe određuje zavisnost tačke ključanja tečnosti od spoljašnjeg pritiska. U jednadžbi (3.3.10)
je promjena tačke ključanja kada se vanjski pritisak promijeni za . Stoga se kriva ravnoteže tekućina-para naziva i kriva ključanja.
52. Van der Waalsova jednačina - Jednačina stanja neidealnih plinova. Eksperimentalno određivanje konstanti van der Waalsove jednadžbe.
Kao što je ranije napomenuto, pri niskim temperaturama i visokim pritiscima Mendeljejev-Klapejronova jednačina za jedan mol supstance
daje značajna odstupanja od eksperimentalno izmjerenih vrijednosti.
Učinjeni su brojni pokušaji da se pronađe jednačina stanja za stvarnu materiju, koja bi mogla da pokrije, ako ne sva stanja materije, onda barem gasovito i tečno. Od mnogih predloženih jednačina, najpoznatija je van der Waalsova jednačina:
 ,
(3.4.2)
,
(3.4.2)
napisano za jedan mol supstance. Za molove ova jednadžba je:
 .
(3.4.3)
.
(3.4.3)
Konstante se određuju eksperimentalno i imaju različite vrijednosti za različite vrste molekula. Jednačina (3.4.2) nije izvedena, već se uspostavlja uvođenjem dvije korekcije u već poznatu Mendeljejev-Klapejronovu jednačinu. Da bismo opravdali njihovo uvođenje, napominjemo da u jednačini (3.4.2) zapremina označava zapreminu posude koja sadrži jedan mol gasa. U slučaju idealnog plina koji se sastoji od materijalnih tačaka, cijeli ovaj volumen je dostupan za kretanje molekula. U pravom plinu, same molekule zauzimaju određeni dio zapremine posude, a taj dio je nedostupan svim ostalim molekulima. Ovaj dio volumena treba oduzeti od volumena. Tada jednačina (3.4.2) poprima oblik
. (3.4.4)
Iz posljednjeg izraza je jasno da je korekcija jednaka volumenu koji bi plin zauzeo pri beskonačno visokom tlaku, tj. molekuli stvarnog plina ne mogu se približiti jedni drugima na razdaljinu jednaku nuli, čak ni pri beskonačno visokom tlaku. Dakle, uvođenje korekcije znači približno uzimanje u obzir odbojnih sila između molekula.
Kao što znamo, između molekula ne djeluju samo odbojne sile, već i sile privlačnosti. Bilo koji molekul koji se nalazi blizu zida posude doživljava neto silu privlačenja
sa strane molekula koji se nalaze u sferi djelovanja privlačnih sila (sl. 51).

Odaberimo platformu na površini zida. Neka na njemu budu molekuli. Zatim rezultirajuća sila koja djeluje na molekule ovog područja iz plina
 ,
(3.4.6)
,
(3.4.6)
pošto iz uslova simetrije sve sile imaju istu veličinu i pravac. Ako silu podijelimo s površinom, dobivamo takozvani molekularni tlak, kojim molekule smještene na zidu djeluju na ostatak mase plina:
. (3.4.7)
Svaki od faktora u formuli (3.4.7) je očigledno proporcionalan gustini gasa, koja je, pak, obrnuto proporcionalna zapremini gasa, tako da možemo napisati:
, (3.4.8)
Gdje a– pozitivni konstantni koeficijent.
Tako će, kao rezultat djelovanja privlačnih sila, pritisak na zid sa strane gasa biti manji od pritiska (3.4.4) koji bi zid doživeo da između molekula nema privlačnih sila, tj.
![]() .
.
Gdje nalazimo van der Waalsovu jednačinu:
 .
(3.4.9)
.
(3.4.9)
Objasnimo pojavu dodatnog pritiska u formuli (3.4.9). Neka plin bude u cilindru ispod bestežinskog klipa. Spoljni pritisak teži da komprimuje gas, odnosno da približi njegove molekule. Ako se molekuli plina ne privlače jedni druge, plin bi iskusio samo vanjski pritisak. Ali međusobna privlačnost molekula, kako smo saznali, također teži približavanju molekula jedni drugima, odnosno djeluje u istom smjeru kao i vanjski pritisak. Stoga se rezultat privlačenja molekula ogleda u očiglednom povećanju vanjskog pritiska na plin, kao da je pritisku na klip dodan neki dodatni pritisak.
Eksperimentalno određivanje konstanti van der Waalsove jednadžbe
Za eksperimentalno određivanje konstanti a a ispitivani gas se stavlja u posudu zatvorene zapremine sa ugrađenim manometrom i pritisak ovog gasa se meri na različitim temperaturama. Numeričkim diferencijacijom eksperimentalno dobijene krive određujemo parcijalni izvod. Iz van der Waalsove jednadžbe nalazimo ovaj izvod
 .
(3.5.1)
.
(3.5.1)
Odavde dobijamo vrijednost:
. (3.5.2)
Zamjenom izraza (3.5.2) u van der Waalsovu jednačinu (3.4.9) izračunavamo drugu veličinu a:
![]() .
(3.5.3)
.
(3.5.3)
Iskustvo je pokazalo da su vrijednosti a i nisu konstantne, ali zavise od temperature, iako slabo. U proračunima se koristi van der Waalsova jednačina, kao konstante a i uzmite prosječne vrijednosti funkcija i u temperaturnom rasponu od interesa


53. Izoterme van der Waalsove jednadžbe i njihovo poređenje s eksperimentalnim izotermama. Određivanje kritičnih parametara supstance iz VdW jednačine. Metastabilna stanja materije su prezasićena para i pregrijana tečnost. Wilsonova komora i mjehurasta komora.
Na sl. 52 prikazuje van der Waalsove izoterme gasa.
Na vrlo visokim temperaturama imaju oblik blizak hiperboli; ove izoterme karakteriziraju plinovito stanje tvari (skoro idealan plin). Kako temperatura opada, oblik izoterme se mijenja i na određenoj temperaturi (kritičnoj) detektira točku savijanja krivulje. Na još nižim temperaturama (podkritičnim), umjesto horizontalnog presjeka koji odgovara faznom prijelazu tekućina-para, izoterme imaju valoviti presjek (Sl. 53).


Rice. 52 R i str. 53
Mjerenja pokazuju da se izoterme stvarne materije praktično poklapaju sa van der Waalsovom izotermom u presjecima (gasovito stanje) i (tečno stanje). Međutim, u srednjem dijelu, umjesto horizontalnog dijela 51, koji odgovara faznom prijelazu tekućina-para, van der Waalsova izoterma ima valoviti dio. Ovaj valoviti dio karakterizira se kako slijedi. Odeljak 12 odgovara metastabilnom stanju pare (prezasićena para), a deo 54 odgovara metastabilnom stanju tečnosti (pregrejana tečnost). U tački 1 postoji samo zasićena para, a u tački 5 samo je ključala tečnost. Što se tiče dijela 234 valovite krivulje, to je fizički nemoguće, jer u prirodi ne postoje tvari za koje bi pri konstantnoj temperaturi povećanje volumena dovelo do povećanja tlaka. Potonje je moguće samo ako temperatura u ovom području nije konstantna. Prezasićena para (odjeljak 12) je plinovito stanje tvari u kojoj je tlak str veći od pritiska zasićene pare na datoj temperaturi - može se dobiti eksperimentalno kompresijom čistog gasa na pritisak veći od pritiska zasićene pare i neće kondenzovati. Stanje prezasićene pare, iako ima određenu stabilnost, manje je stabilno od dvofaznog stanja (izobar 135), u kojem je, kao što znamo, dio tvari u obliku tekućine, a dio u obliku zasićene pare. Stoga, uz blagi vanjski utjecaj, prezasićena para djelomično prelazi u tekućinu, a preostala para postaje zasićena.
Pregrijana tečnost (odjeljak 45) - stanje koje karakterizira činjenica da postoji pri pritisku nižem od tlaka zasićene pare na datoj temperaturi - može se dobiti produženim ključanjem čiste tekućine, uslijed čega se stvaraju mjehurići plina (jezgra isparavanje) uklanjaju se iz tečnosti, a tečnost se zagreva na temperaturu iznad tačke ključanja pri datom pritisku. Ispostavilo se da je i stanje pregrijane tekućine manje stabilno od stanja ravnoteže između tekućine i zasićene pare. Ako se u tako pregrijanu tekućinu unesu čestice strane tvari, ona brzo prelazi u dvofazno stanje.
Stanja prezasićene pare i pregrijane tekućine koriste se u instrumentima nuklearne fizike (oblačna komora i komora s mjehurićima) za snimanje i mjerenje parametara elementarnih čestica.
Ako se na van der Waalsovoj izotermi valoviti dio zamijeni nekom horizontalnom ravnom linijom 135, tada će izoterma dobivena na ovaj način kvalitativno ispravno opisivati dvofazno stanje tvari. Položaj ove linije može se odrediti ako se drugi zakon termodinamike u Klauzijevoj notaciji (2.13.7) primijeni na zatvoreni reverzibilni ciklus 1234531:
. (3.6.1)
Budući da duž cijelog puta 1234531 temperatura tvari ostaje nepromijenjena (budući da se ovaj put sastoji od odsječaka dvije moguće varijante iste izoterme), posljednja jednačina se može napisati u obliku
. (3.6.5) sa eksperimentalnim podacima pokazuju da je van der Waalsova jednačina, iz koje se dobija ova vrijednost, približna, iako je kvalitativnu sliku promjene stanja materije jednačina sasvim korektno prenijela. Postoji veliki broj pokušaja da se dobije tačnija jednačina stanja materije. Međutim, ove jednačine sadrže veliki broj faktora korekcije čije je fizičko značenje nejasno, kao u van der Waalsovoj jednačini.
U najopštijem obliku, koristeći metode statističke fizike, akademik N. N. Bogolyubov je dobio jednačinu stanja
 ,
(3.6.12)
,
(3.6.12)
gdje su takozvani viralni koeficijenti, koji su funkcije samo temperature. Iz jednadžbe Bogolyubova slijedi da što je veća vrijednost molarne zapremine, manji broj članova serije treba uzeti u obzir da bi se dobio prilično tačan rezultat. Kada svi članovi redova stepena nestanu, a jednačina (3.6.12) dobije oblik , tj., kako bi se očekivalo, jednačina Bogoljubova se pretvara u Mendeljejev-Klapejronovu jednačinu. Virijalni koeficijenti se ne mogu izračunati čisto teorijskim metodama i stoga se moraju odrediti korištenjem eksperimentalnih podataka. Međutim, pokazalo se da je ovaj problem toliko složen da je prikladnije dobiti jednadžbu stanja jednostavno u obliku interpolacijske formule koja opisuje eksperimentalne podatke.
Određivanje toplote isparavanja tečnosti
Za ravnotežu između tečnosti i pare, Clapeyron-Clausiusova jednačina se može izvesti na sledeći način.
Prema drugom zakonu termodinamike, ako je sistem u ravnoteži, onda pod datim uslovima ( R, T) nijedan posao nije obavljen
Ap = 0; G i -G P = 0; G i = G P (2)
odnosno Gibbsove slobodne energije čiste tečnosti i njene pare su jednake (ovo su uslovi ravnoteže).
Promenimo jedan od uslova koji određuju ravnotežu, na primer temperaturu (tj. grejemo sistem T), kao rezultat toga će se uspostaviti novi pritisak, nova ravnoteža tekućina-para:
G " i = G " P (3)
ili G i = G P (4)
Ako dođe do promjene vanjskog parametra za beskonačno mali iznos - dT, tada će se izobarično-izotermni potencijali promijeniti za beskonačno malu vrijednost:
dG i =dG P (5)
Izobarično-izotermni potencijal predstavlja slobodnu energiju sistema i funkcija je pritiska i temperature:
dG=VdP–SDT(6)
stoga se može koristiti za uspostavljanje kvantitativne veze između pritiska zasićene pare i temperature.
Nakon zamjene (6) u (5) nalazimo se u ravnotežnom stanju
V i dP-S i dT = V P dP-S P dT(7)
odakle (8)
Gdje ( S P -S i) I ( V P - V i) - promjena entropije i zapremine sistema tokom prelaska supstance iz tečnog u parno stanje. Prema drugom zakonu termodinamike, promena entropije sistema tokom isparavanja jednaka je smanjenoj toploti isparavanja
 (9)
(9)
Zamjenom izraza (9) u (8) dobijamo
 (10)
(10)
gdje je ∆ H isp i ∆ V isp- respektivno, promena entalpije i zapremine tokom isparavanja, i T bale- temperatura ključanja.
Jednadžba (10) nazvana Clapeyron-Clausiusova jednačina . Prema (10), nagib linija u faznom dijagramu vode (slika 1) određen je predznakom izvoda dP/dT ili njegova recipročna dT/dP- karakteriziranje promjene temperature s povećanjem pritiska.
Od faznih prelaza smatramo isparavanje i taljenje. Toplota isparavanja - prijelaz tekuće faze u plinovitu fazu - je pozitivna. Molarna toplota isparavanja je količina topline koja se troši da ispari jedan mol tekuće tvari. Volumen gasa tokom isparavanja je uvek veći od odgovarajuće zapremine tečnosti, odnosno u jednačini (10) V P >V i. Zbog toga dP/dT, i zbog toga dT/dP također su uvijek pozitivni ( dT/dP> 0). Posljedično, temperatura isparavanja uvijek raste s povećanjem tlaka (kriva uredu na sl. 1 ili pogledajte tabelu. 1 Dodatak). Sa povećanjem temperature, pritisak zasićene pare iznad tečnosti raste, dostižući svoju maksimalnu vrednost na kritičnoj temperaturi. Ovo posljednje je granična temperatura (na primjer, za vodu je 374,12 o C) pri kojoj je moguća ravnoteža između tekuće i parne faze tvari. Na višim temperaturama supstanca može biti samo u gasovitom stanju, a pojam zasićene pare gubi smisao.
Toplota fuzije - prijelaz čvrste faze u tečnu fazu je također uvijek pozitivan.

Rice. 1. Dijagram stanja vode pri niskim pritiscima
Regioni: 1 - čvrsta faza (led); II- tečnost; III - par.
Krive: AO - sublimacija; OK - isparavanje; OV - topljenje.
O je trostruka tačka koja odgovara ravnoteži tri faze.
Zapremina tečne faze u opštem slučaju može biti veća ili manja od zapremine iste količine čvrste faze. Odavde, u skladu sa jednačinom (10), slijedi da je vrijednost dP/dT ili njegovu inverznu vrijednost dT/dP, može biti pozitivan ili negativan. To znači da tačka topljenja može porasti ili pasti s povećanjem pritiska. Magnituda dT/dP pozitivno na većinu supstanci. Ima negativnu vrijednost samo za vodu, bizmut i nekoliko drugih tvari kod kojih je gustina tekućine na tački tališta veća od gustine čvrste faze ( V i -V T) < 0. В связи с этим при увеличении давления температура плавления льда понижается (криваяOB).
Treba napomenuti da razmatrani obrasci vrijede za niske pritiske.
Clapeyron-Clausiusova jednačina (10) može se transformirati uzimanjem sljedećih aproksimacija:
1) Kako je ∆ V isp =(V P -V i) >> 0 (na primjer, za vodu, molarni volumen u stanju pare na br. V P≈ 22400 cm 2, iu tečnom stanju V i≈ 18 cm 3), tada bez velike greške možemo zanemariti vrijednost V i i prihvatimo da ∆ V isp ≈ V P .
2) Na ne previsokim pritiscima i temperaturama (daleko od kritičnih), jednačina stanja idealnih gasova se može primeniti na realne sisteme. Dobijena greška u ovom slučaju ispada beznačajna.
 (11)
(11)
Zamjenom (11) u (10) dobijamo:
 (12)
(12)
koji nakon transformacije
 (13)
(13)
poprima oblik
 (14)
(14)
Toplota isparavanja zavisi od temperature : Kako temperatura raste, toplota isparavanja se smanjuje. Na kritičnoj temperaturi, toplota isparavanja je nula. Međutim, na temperaturama daleko od kritičnih, promjene ∆ N isp sa temperaturom nisu baš sjajni. U ne previše širokom temperaturnom rasponu∆ N isp može se smatrati konstantnim.
Integracija Clapeyron-Clausiusove jednadžbe (14) unutar temperaturnog raspona T 1 i T 2, koji odgovaraju pritiscima R 1 i R 2 pri konstanti ∆ N isp, daje
 (15)
(15)
ili pri prelasku na decimalne logaritme
 (16)
(16)
(R- univerzalna plinska konstanta jednaka 8,314 J/mol K).
Jednačine (15), (16) nam omogućavaju da izračunamo toplotu isparavanja. Da biste to učinili, na temelju eksperimentalnih podataka, gradi se ovisnost lnP=f(1/T) ili lgP=f(1/T) i odaberite dvije tačke na rezultirajućoj pravoj liniji (slika 2). Zamijenite vrijednosti logaritma pritiska i inverzne temperature koje odgovaraju ovim tačkama u jednadžbu (17):
 (17)
(17)
∆ vrijednost N isp prema jednačini (17) zavisi od uzetog temperaturnog intervala i što je bliži pravom, to je ovaj interval manji. Međutim, takav proračun zahtijeva vrlo precizna mjerenja tačke ključanja i pritiska pare.
Za izračunavanje ∆ N isp u relativno širokom temperaturnom rasponu (50...100 o C), trebali biste odabrati tačke koje najpreciznije odgovaraju pravoj liniji lgP=f(1/T).
Tačka ključanja tečnosti, pritisak pare na datoj temperaturi i toplota isparavanja su specifične konstante materije , čije su vrijednosti neophodne za mnoge teorijske i praktične proračune. Na osnovu ovih podataka moguće je odrediti čistoću hemikalija, izračunati razdvajanje smeša destilacijom i izračunati troškove energije za isparavanje tečnosti potrebne za izvođenje reakcije u gasnoj fazi.
Izračunavanje topline isparavanja pomoću molekularnih parametara uvijek uključuje pretpostavke. Približan je i prikladan ako je ispunjen niz uslova. Međutim, postoji fundamentalna Clapeyron-Clausiusova jednačina koja povezuje toplinu isparavanja sa drugim termodinamičkim karakteristikama sistema i dobijena je striktno na osnovu drugog zakona termodinamike.
Neka radna tvar koja izvodi Carnotov ciklus bude dvofazni parni sistem zasićen tekućinom. Početno stanje takvog sistema prikazujemo kao tačku 1 na slici 8.17. Izvršimo izobarično-izotermno širenje sistema na temperaturi od stanja 1 do stanja 2. U tom slučaju će određena masa tečnosti ispariti i, shodno tome, apsorbovaće se toplota jednaka toploti isparavanja tečnosti od termostata. Razlika u zapreminama u tačkama 2 i 1 jednaka je razlici zapremina u gasovitom i tečnom stanju za isparenu masu supstance: Iz stanja 2, dvofazni sistem se adijabatski prelazi u stanje 3 sa nižom temperaturom od 7%. Iz stanja 3 radna tvar se izobarično-izotermički prelazi u stanje 4, dok se dio para kondenzira i toplina se oslobađa u hladnjak.Iz stanja 4 dvofazni sistem se adijabatskom kompresijom prenosi u početno stanje. Rad u ciklusu je:
gdje je efikasnost ciklusa
![]()
Pri malim razlikama temperatura (pritisaka) rad ciklusa je jednak:
Koristeći (83.3) i (83.2), prepisujemo (83.1):
![]()
Zamjenom i prolaskom do granice dobijamo:
![]()
Ovaj odnos je pronašao francuski inženjer Clapeyron (1832) prije nego što je uspostavljen prvi zakon termodinamike.

Modernu derivaciju ove jednačine dao je Clausius, zbog čega se naziva Clapeyron-Clausiusova jednačina. Ova jednadžba vam omogućava da izračunate toplinu isparavanja (specifična, molarna), ako su poznati ovisnost tlaka zasićene pare o temperaturi, te zapremine tekućine i pare (specifične, molarne).
Derivat se određuje iz eksperimentalno utvrđene zavisnosti (ovisnost pritiska zasićene pare o temperaturi).
Clapeyron-Clausiusova jednačina vrijedi ne samo za prijelaz tekućina-para, već i za sve druge fazne prijelaze. Izražava promjenu tlaka pri kojoj je faza u ravnoteži s promjenom temperature. Dakle, za topljenje, jednačina (83.4) poprima oblik
![]()