Logaritms no skaitļa 8 līdz bāzei 4. Kas ir logaritms. Kā uzrakstīt skaitli kā logaritmu

Jūsu privātuma saglabāšana mums ir svarīga. Šī iemesla dēļ mēs esam izstrādājuši Privātuma politiku, kurā aprakstīts, kā mēs izmantojam un uzglabājam jūsu informāciju. Lūdzu, pārskatiet mūsu privātuma praksi un informējiet mūs, ja jums ir kādi jautājumi.

Personiskās informācijas vākšana un izmantošana

Personiskā informācija attiecas uz datiem, kurus var izmantot, lai identificētu vai sazinātos ar konkrētu personu.

Jums var tikt lūgts sniegt savu personisko informāciju jebkurā laikā, kad sazināsieties ar mums.

Tālāk ir sniegti daži piemēri par to, kāda veida personas informāciju mēs varam vākt un kā mēs varam izmantot šādu informāciju.

Kādu personas informāciju mēs apkopojam:

• Kad jūs iesniedzat pieteikumu vietnē, mēs varam apkopot dažādu informāciju, tostarp jūsu vārdu, tālruņa numuru, e-pasta adresi utt.

Kā mēs izmantojam jūsu personisko informāciju:

• Mūsu apkopotā personas informācija ļauj mums sazināties ar jums par unikāliem piedāvājumiem, akcijām un citiem notikumiem un gaidāmajiem pasākumiem.
• Laiku pa laikam mēs varam izmantot jūsu personisko informāciju, lai nosūtītu svarīgus paziņojumus un paziņojumus.
• Mēs varam izmantot personas informāciju arī iekšējiem mērķiem, piemēram, auditu, datu analīzes un dažādu pētījumu veikšanai, lai uzlabotu mūsu sniegtos pakalpojumus un sniegtu jums ieteikumus par mūsu pakalpojumiem.
• Ja jūs piedalāties balvu izlozē, konkursā vai līdzīgā akcijā, mēs varam izmantot jūsu sniegto informāciju šādu programmu administrēšanai.

Informācijas izpaušana trešajām personām

Mēs neizpaužam no jums saņemto informāciju trešajām personām.

Izņēmumi:

• Ja nepieciešams - saskaņā ar likumu, tiesas procedūru, tiesvedībā un/vai pamatojoties uz publiskiem pieprasījumiem vai valdības iestāžu lūgumiem Krievijas Federācijas teritorijā - izpaust savu personas informāciju. Mēs varam arī izpaust informāciju par jums, ja konstatēsim, ka šāda izpaušana ir nepieciešama vai piemērota drošības, tiesībaizsardzības vai citiem sabiedrībai svarīgiem mērķiem.
• Reorganizācijas, apvienošanas vai pārdošanas gadījumā mēs varam nodot mūsu apkopoto personas informāciju attiecīgajai trešajai pusei.

Personiskās informācijas aizsardzība

Mēs veicam piesardzības pasākumus, tostarp administratīvus, tehniskus un fiziskus, lai aizsargātu jūsu personisko informāciju pret pazaudēšanu, zādzību un ļaunprātīgu izmantošanu, kā arī no nesankcionētas piekļuves, izpaušanas, pārveidošanas un iznīcināšanas.

Jūsu privātuma ievērošana uzņēmuma līmenī

Lai nodrošinātu jūsu personiskās informācijas drošību, mēs saviem darbiniekiem paziņojam par privātuma un drošības standartiem un stingri īstenojam privātuma praksi.

Kā zināms, reizinot izteiksmes ar pakāpēm, to eksponenti vienmēr summējas (a b *a c = a b+c). Šo matemātisko likumu atvasināja Arhimēds, un vēlāk, 8. gadsimtā, matemātiķis Virasens izveidoja veselo skaitļu eksponentu tabulu. Tieši viņi kalpoja turpmākai logaritmu atklāšanai. Šīs funkcijas izmantošanas piemērus var atrast gandrīz visur, kur nepieciešams vienkāršot apgrūtinošo reizināšanu ar vienkāršu saskaitīšanu. Ja veltīsiet 10 minūtes šī raksta lasīšanai, mēs jums paskaidrosim, kas ir logaritmi un kā ar tiem strādāt. Vienkāršā un pieejamā valodā.

Definīcija matemātikā

Logaritms ir šādas formas izteiksme: log a b=c, tas ir, jebkura nenegatīva skaitļa (tas ir jebkura pozitīva) logaritms “b” līdz tā bāzei “a” tiek uzskatīts par pakāpju “c”. ”, līdz kuram jāpaaugstina bāze “a”, lai galu galā iegūtu vērtību “b”. Analizēsim logaritmu, izmantojot piemērus, pieņemsim, ka ir izteiksme log 2 8. Kā atrast atbildi? Tas ir ļoti vienkārši, jums ir jāatrod tāda jauda, ​​lai no 2 līdz vajadzīgajai jaudai iegūtu 8. Pēc dažu aprēķinu veikšanas galvā mēs iegūstam skaitli 3! Un tā ir taisnība, jo 2 līdz 3 dod atbildi kā 8.

Logaritmu veidi

Daudziem skolēniem un studentiem šī tēma šķiet sarežģīta un nesaprotama, taču patiesībā logaritmi nav tik biedējoši, galvenais ir saprast to vispārējo nozīmi un atcerēties to īpašības un dažus noteikumus. Ir trīs atsevišķi logaritmisko izteiksmju veidi:

1. Naturālais logaritms ln a, kur bāze ir Eilera skaitlis (e = 2,7).
2. Decimāldaļa a, kur bāze ir 10.
3. Jebkura skaitļa b logaritms uz bāzi a>1.

Katrs no tiem tiek atrisināts standarta veidā, ieskaitot vienkāršošanu, samazināšanu un sekojošu samazināšanu līdz vienam logaritmam, izmantojot logaritmiskās teorēmas. Lai iegūtu pareizās logaritmu vērtības, risinot tos, jāatceras to īpašības un darbību secība.

Noteikumi un daži ierobežojumi

Matemātikā ir vairāki noteikumi-ierobežojumi, kas tiek pieņemti kā aksioma, tas ir, tie nav diskutējami un ir patiesība. Piemēram, nav iespējams dalīt skaitļus ar nulli, kā arī nav iespējams iegūt negatīvo skaitļu pāra sakni. Logaritmiem ir arī savi noteikumi, pēc kuriem jūs varat viegli iemācīties strādāt pat ar garām un ietilpīgām logaritmiskām izteiksmēm:

• Bāzei “a” vienmēr jābūt lielākai par nulli, nevis vienādai ar 1, pretējā gadījumā izteiksme zaudēs savu nozīmi, jo “1” un “0” jebkurā pakāpē vienmēr ir vienādi ar to vērtībām;
• ja a > 0, tad a b >0, izrādās, ka arī “c” ir jābūt lielākam par nulli.

Kā atrisināt logaritmus?

Piemēram, ir dots uzdevums atrast atbildi uz vienādojumu 10 x = 100. Tas ir ļoti vienkārši, jums jāizvēlas jauda, ​​paaugstinot skaitli desmit, līdz kuram mēs iegūstam 100. Tas, protams, ir 10 2 = 100.

Tagad attēlosim šo izteiksmi logaritmiskā formā. Iegūstam log 10 100 = 2. Atrisinot logaritmus, visas darbības praktiski saplūst, lai atrastu jaudu, līdz kurai jāievada logaritma bāze, lai iegūtu doto skaitli.

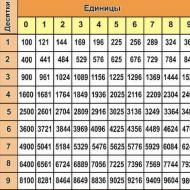
Lai precīzi noteiktu nezināmas pakāpes vērtību, jums jāiemācās strādāt ar grādu tabulu. Tas izskatās šādi:

Kā redzat, dažus eksponentus var uzminēt intuitīvi, ja jums ir tehnisks prāts un zināšanas par reizināšanas tabulu. Tomēr lielākām vērtībām jums būs nepieciešams strāvas galds. To var izmantot pat tie, kas neko nezina par sarežģītām matemātikas tēmām. Kreisajā kolonnā ir skaitļi (bāze a), augšējā skaitļu rinda ir jaudas c vērtība, līdz kurai tiek pacelts skaitlis a. Krustojumā šūnās ir skaitļu vērtības, kas ir atbilde (a c = b). Ņemsim, piemēram, pašu pirmo šūnu ar skaitli 10 un kvadrātā, iegūstam vērtību 100, kas norādīta mūsu divu šūnu krustpunktā. Viss ir tik vienkārši un viegli, ka sapratīs pat visīstākais humānists!

Vienādojumi un nevienādības

Izrādās, ka noteiktos apstākļos eksponents ir logaritms. Tāpēc jebkuras matemātiskas skaitliskas izteiksmes var uzrakstīt kā logaritmisku vienādību. Piemēram, 3 4 =81 var uzrakstīt kā 81 bāzes 3 logaritmu, kas vienāds ar četriem (log 3 81 = 4). Negatīvām pakāpēm noteikumi ir vienādi: 2 -5 = 1/32 rakstām kā logaritmu, iegūstam log 2 (1/32) = -5. Viena no aizraujošākajām matemātikas sadaļām ir “logaritmu” tēma. Tālāk mēs apskatīsim vienādojumu piemērus un risinājumus, tūlīt pēc to īpašību izpētes. Tagad apskatīsim, kā izskatās nevienlīdzības un kā tās atšķirt no vienādojumiem.

Tiek dota šāda izteiksme: log 2 (x-1) > 3 - tā ir logaritmiska nevienādība, jo nezināmā vērtība “x” atrodas zem logaritmiskās zīmes. Un arī izteiksmē tiek salīdzināti divi lielumi: vēlamā skaitļa logaritms bāzei divi ir lielāks par skaitli trīs.

Būtiskākā atšķirība starp logaritmiskiem vienādojumiem un nevienādībām ir tā, ka vienādojumi ar logaritmiem (piemēram, logaritms 2 x = √9) atbildē ietver vienu vai vairākas konkrētas skaitliskās vērtības, savukārt, risinot nevienādību, abas pieļaujamās vērtības. vērtības un punkti tiek noteikti, pārkāpjot šo funkciju. Rezultātā atbilde nav vienkārša atsevišķu skaitļu kopa, kā vienādojuma atbildē, bet gan nepārtraukta skaitļu virkne vai kopa.

Pamatteorēmas par logaritmiem

Risinot primitīvus logaritma vērtību atrašanas uzdevumus, tā īpašības var nebūt zināmas. Taču, runājot par logaritmiskiem vienādojumiem vai nevienādībām, pirmkārt, ir skaidri jāsaprot un jāpiemēro praksē visas logaritmu pamatīpašības. Vienādojumu piemērus apskatīsim vēlāk; vispirms apskatīsim katru īpašumu sīkāk.

1. Galvenā identitāte izskatās šādi: a logaB =B. To piemēro tikai tad, ja a ir lielāks par 0, nav vienāds ar vienu, un B ir lielāks par nulli.
2. Produkta logaritmu var attēlot ar šādu formulu: log d (s 1 * s 2) = log d s 1 + log d s 2. Šajā gadījumā obligāts nosacījums ir: d, s 1 un s 2 > 0; a≠1. Jūs varat sniegt pierādījumu šai logaritmiskajai formulai ar piemēriem un risinājumu. Pieņemsim, ka log a s 1 = f 1 un log a s 2 = f 2, tad a f1 = s 1, a f2 = s 2. Iegūstam, ka s 1 * s 2 = a f1 *a f2 = a f1+f2 (īpašības grādi ), un pēc tam pēc definīcijas: log a (s 1 * s 2) = f 1 + f 2 = log a s1 + log a s 2, kas ir tas, kas bija jāpierāda.
3. Koeficienta logaritms izskatās šādi: log a (s 1/ s 2) = log a s 1 - log a s 2.
4. Teorēma formulas formā iegūst šādu formu: log a q b n = n/q log a b.

Šo formulu sauc par "logaritma pakāpes īpašību". Tas atgādina parasto grādu īpašības, un tas nav pārsteidzoši, jo visa matemātika balstās uz dabiskiem postulātiem. Apskatīsim pierādījumu.

Lai log a b = t, izrādās a t =b. Ja abas daļas paaugstinām pakāpē m: a tn = b n ;

bet tā kā a tn = (a q) nt/q = b n, tāpēc log a q b n = (n*t)/t, tad log a q b n = n/q log a b. Teorēma ir pierādīta.

Problēmu un nevienlīdzību piemēri

Visizplatītākie logaritmu problēmu veidi ir vienādojumu un nevienādību piemēri. Tie ir atrodami gandrīz visās uzdevumu grāmatās, kā arī ir obligāta matemātikas eksāmenu sastāvdaļa. Lai iestātos augstskolā vai nokārtotu iestājpārbaudījumus matemātikā, jums jāzina, kā pareizi atrisināt šādus uzdevumus.

Diemžēl nav vienota plāna vai shēmas logaritma nezināmās vērtības risināšanai un noteikšanai, taču katrai matemātiskajai nevienādībai vai logaritmiskajam vienādojumam var piemērot noteiktus noteikumus. Pirmkārt, jums vajadzētu noskaidrot, vai izteiksmi var vienkāršot vai samazināt līdz vispārīgai formai. Jūs varat vienkāršot garās logaritmiskās izteiksmes, ja pareizi izmantojat to īpašības. Ātri iepazīsim tos.

Risinot logaritmiskos vienādojumus, ir jānosaka, kāda veida logaritms mums ir: izteiksmes piemērs var saturēt naturālo logaritmu vai decimāldaļu.

Šeit ir piemēri ln100, ln1026. Viņu risinājums ir saistīts ar faktu, ka viņiem ir jānosaka jauda, ​​kurai bāze 10 būs attiecīgi vienāda ar 100 un 1026. Lai atrisinātu naturālos logaritmus, jāpiemēro logaritmiskās identitātes vai to īpašības. Apskatīsim dažādu veidu logaritmisko problēmu risināšanas piemērus.

Kā lietot logaritma formulas: ar piemēriem un risinājumiem

Tātad, aplūkosim logaritmu pamata teorēmu izmantošanas piemērus.

1. Produkta logaritma īpašību var izmantot uzdevumos, kur nepieciešams lielu skaitļa b vērtību sadalīt vienkāršākos faktoros. Piemēram, log 2 4 + log 2 128 = log 2 (4*128) = log 2 512. Atbilde ir 9.
2. log 4 8 = log 2 2 2 3 = 3/2 log 2 2 = 1,5 - kā redzat, izmantojot logaritma jaudas ceturto īpašību, mums izdevās atrisināt šķietami sarežģītu un neatrisināmu izteiksmi. Jums vienkārši jāaprēķina bāze un pēc tam jāizņem eksponenta vērtības no logaritma zīmes.

Vienotā valsts eksāmena uzdevumi

Logaritmi bieži sastopami iestājeksāmenos, īpaši daudz logaritmisku uzdevumu Vienotajā valsts eksāmenā (valsts eksāmens visiem skolas absolventiem). Parasti šie uzdevumi ir ne tikai A daļā (vieglākā eksāmena testa daļa), bet arī C daļā (sarežģītākie un apjomīgākie uzdevumi). Eksāmenam nepieciešamas precīzas un nevainojamas zināšanas par tēmu “Dabas logaritmi”.

Problēmu piemēri un risinājumi ir ņemti no vienotā valsts eksāmena oficiālajām versijām. Redzēsim, kā šādi uzdevumi tiek risināti.

Dotais log 2 (2x-1) = 4. Risinājums:
pārrakstīsim izteiksmi, nedaudz vienkāršojot log 2 (2x-1) = 2 2, pēc logaritma definīcijas iegūstam, ka 2x-1 = 2 4, tātad 2x = 17; x = 8,5.

• Vislabāk visus logaritmus samazināt līdz vienai bāzei, lai risinājums nebūtu apgrūtinošs un mulsinošs.
• Visas izteiksmes zem logaritma zīmes tiek norādītas kā pozitīvas, tāpēc, kad izteiksmes eksponents, kas atrodas zem logaritma zīmes un kā tās bāze, tiek izņemts kā reizinātājs, izteiksmei, kas paliek zem logaritma, jābūt pozitīvai.

\(a^(b)=c\) \(\bultiņa pa kreisi\) \(\log_(a)(c)=b\)

Paskaidrosim vienkāršāk. Piemēram, \(\log_(2)(8)\) ir vienāds ar jaudu, līdz kurai jāpalielina \(2\), lai iegūtu \(8\). No tā ir skaidrs, ka \(\log_(2) (8)=3\).

Arguments un logaritma bāze

Jebkuram logaritmam ir šāda “anatomija”:

Logaritma argumentu parasti raksta tā līmenī, un bāzi raksta ar apakšindeksu tuvāk logaritma zīmei. Un šis ieraksts skan šādi: "logaritms no divdesmit pieci līdz pieci."

Kā aprēķināt logaritmu?

Lai aprēķinātu logaritmu, jāatbild uz jautājumu: līdz kādai jaudai jāpaaugstina bāze, lai iegūtu argumentu?

Piemēram, aprēķiniet logaritmu: a) \(\log_(4)(16)\) b) \(\log_(3)\)\(\frac(1)(3)\) c) \(\log_(\) sqrt (5)) (1)\) d) \(\log_(\sqrt(7))(\sqrt(7))\) e) \(\log_(3)(\sqrt(3))\)

a) Uz kādu jaudu jāpaaugstina \(4\), lai iegūtu \(16\)? Acīmredzot otrais. Tāpēc:

\(\log_(4)(16)=2\)

\(\log_(3)\)\(\frac(1)(3)\) \(=-1\)

c) Uz kādu jaudu jāpalielina \(\sqrt(5)\), lai iegūtu \(1\)? Kāds spēks padara jebkuru pirmo numuru? Nulle, protams!

\(\log_(\sqrt(5))(1)=0\)

d) Uz kādu jaudu jāpalielina \(\sqrt(7)\), lai iegūtu \(\sqrt(7)\)? Pirmkārt, jebkurš skaitlis ar pirmo pakāpi ir vienāds ar sevi.

\(\log_(\sqrt(7))(\sqrt(7))=1\)

e) Uz kādu jaudu jāpalielina \(3\), lai iegūtu \(\sqrt(3)\)? Mēs zinām, ka tas ir daļskaitlis, kas nozīmē, ka kvadrātsakne ir \(\frac(1) (2)\) jauda.

\(\log_(3)(\sqrt(3))=\)\(\frac(1)(2)\)

Piemērs : Aprēķināt logaritmu \(\log_(4\sqrt(2))(8)\)

Risinājums :

Atbilde : \(\log_(4\sqrt(2))(8)=1,2\)

Kāpēc tika izgudrots logaritms?

Lai to saprastu, atrisināsim vienādojumu: \(3^(x)=9\). Vienkārši saskaņojiet \(x\), lai vienādojums darbotos. Protams, \(x=2\).

Tagad atrisiniet vienādojumu: \(3^(x)=8\). Ar ko x ir vienāds? Tā ir būtība.

Gudrākie teiks: "X ir nedaudz mazāks par diviem." Kā tieši uzrakstīt šo numuru? Lai atbildētu uz šo jautājumu, tika izgudrots logaritms. Pateicoties viņam, atbildi šeit var uzrakstīt kā \(x=\log_(3)(8)\).

Es gribu uzsvērt, ka \(\log_(3) (8)\), patīk jebkurš logaritms ir tikai skaitlis. Jā, tas izskatās neparasti, bet ir īss. Jo, ja mēs gribētu to rakstīt kā decimāldaļskaitli, tas izskatītos šādi: \(1.892789260714.....\)

Piemērs : atrisiniet vienādojumu \(4^(5x-4)=10\)

Risinājums :

Atbilde : \(\frac(\log_(4)(10)+4)(5)\)

Decimāllogaritmi un naturālie logaritmi

Kā teikts logaritma definīcijā, tā bāze var būt jebkurš pozitīvs skaitlis, izņemot vienu \((a>0, a\neq1)\). Un starp visām iespējamām bāzēm ir divas, kas sastopamas tik bieži, ka logaritmiem ar tiem tika izgudrots īpašs īss apzīmējums:

Dabiskais logaritms: logaritms, kura bāze ir Eilera skaitlis \(e\) (vienāds ar aptuveni \(2,7182818…\)), un logaritms ir uzrakstīts kā \(\ln(a)\).

Tas ir, \(\ln(a)\) ir tāds pats kā \(\log_(e)(a)\)

Decimālais logaritms: logaritms, kura bāze ir 10, tiek uzrakstīts \(\lg(a)\).

Tas ir, \(\lg(a)\) ir tāds pats kā \(\log_(10)(a)\), kur \(a\) ir kāds skaitlis.

Pamatlogaritmiskā identitāte

Logaritmiem ir daudz īpašību. Viens no tiem tiek saukts par “Pamata logaritmisko identitāti” un izskatās šādi:

Šis īpašums izriet tieši no definīcijas. Redzēsim, kā tieši šī formula radās.

Atcerēsimies īsu logaritma definīcijas apzīmējumu:

ja \(a^(b)=c\), tad \(\log_(a)(c)=b\)

Tas nozīmē, ka \(b\) ir tāds pats kā \(\log_(a)(c)\). Tad mēs varam ierakstīt \(\log_(a)(c)\) nevis \(b\) formulā \(a^(b)=c\). Izrādījās \(a^(\log_(a)(c))=c\) - galvenā logaritmiskā identitāte.

Jūs varat atrast citas logaritmu īpašības. Ar to palīdzību jūs varat vienkāršot un aprēķināt izteiksmju vērtības ar logaritmiem, kuras ir grūti tieši aprēķināt.

Piemērs : atrodiet izteiksmes vērtību \(36^(\log_(6)(5))\)

Risinājums :

Atbilde : \(25\)

Kā uzrakstīt skaitli kā logaritmu?

Kā minēts iepriekš, jebkurš logaritms ir tikai skaitlis. Ir arī otrādi: jebkuru skaitli var uzrakstīt kā logaritmu. Piemēram, mēs zinām, ka \(\log_(2) (4)\) ir vienāds ar divi. Tad divu vietā var rakstīt \(\log_(2)(4)\).

Bet \(\log_(3)(9)\) ir arī vienāds ar \(2\), kas nozīmē, ka mēs varam rakstīt arī \(2=\log_(3)(9)\) . Tāpat ar \(\log_(5)(25)\) un ar \(\log_(9)(81)\) utt. Tas ir, izrādās

\(2=\log_(2)(4)=\log_(3)(9)=\log_(4)(16)=\log_(5)(25)=\log_(6)(36)=\ log_(7)(49)...\)

Tādējādi, ja mums ir nepieciešams, mēs varam ierakstīt divus kā logaritmu ar jebkuru bāzi jebkurā vietā (vienādojumā, izteiksmē vai nevienādībā) - mēs vienkārši rakstām bāzi kvadrātā kā argumentu.

Tas pats ir ar trīskāršu — to var rakstīt kā \(\log_(2)(8)\), vai kā \(\log_(3)(27)\), vai kā \(\log_(4)( 64) \)... Šeit mēs rakstām bāzi kubā kā argumentu:

\(3=\log_(2)(8)=\log_(3)(27)=\log_(4)(64)=\log_(5)(125)=\log_(6)(216)=\ log_(7)(343)...\)

Un ar četriem:

\(4=\log_(2)(16)=\log_(3)(81)=\log_(4)(256)=\log_(5)(625)=\log_(6)(1296)=\ log_(7)(2401)...\)

Un ar mīnus viens:

\(-1=\) \(\log_(2)\)\(\frac(1)(2)\) \(=\) \(\log_(3)\)\(\frac(1)( 3)\) \(=\) \(\log_(4)\)\(\frac(1)(4)\) \(=\) \(\log_(5)\)\(\frac(1) )(5)\) \(=\) \(\log_(6)\)\(\frac(1)(6)\) \(=\) \(\log_(7)\)\(\frac (1) (7)\) \(...\)

Un ar vienu trešdaļu:

\(\frac(1)(3)\) \(=\log_(2)(\sqrt(2))=\log_(3)(\sqrt(3))=\log_(4)(\sqrt( 4))=\log_(5)(\sqrt(5))=\log_(6)(\sqrt(6))=\log_(7)(\sqrt(7))...\)

Jebkuru skaitli \(a\) var attēlot kā logaritmu ar bāzi \(b\): \(a=\log_(b)(b^(a))\)

Piemērs : atrodiet izteiciena nozīmi \(\frac(\log_(2)(14))(1+\log_(2)(7))\)

Risinājums :

Atbilde : \(1\)

Logaritms no dotā skaitļa tiek saukts eksponents, līdz kuram jāpaaugstina cits skaitlis, jāizsauc pamata logaritms, lai iegūtu šo skaitli. Piemēram, 100. bāzes logaritms ir 2. Citiem vārdiem sakot, 10 ir jāliek kvadrātā, lai iegūtu 100 (10 2 = 100). Ja n- dots numurs, b– bāze un l– tad logaritms b l = n. Numurs n sauc arī par bāzes antilogaritmu b cipariem l. Piemēram, antilogaritms no 2 līdz 10. bāzei ir vienāds ar 100. To var uzrakstīt attiecību žurnāla formā. b n = l un antilog b l = n.

Logaritmu pamatīpašības:

Jebkurš pozitīvs skaitlis, kas nav viens, var kalpot par logaritmu bāzi, bet diemžēl izrādās, ka, ja b Un n ir racionālie skaitļi, tad retos gadījumos ir šāds racionāls skaitlis l, Kas b l = n. Tomēr ir iespējams definēt iracionālu skaitli l, piemēram, tā, ka 10 l= 2; tas ir neracionāls skaitlis l var tuvināt ar jebkuru nepieciešamo precizitāti ar racionāliem skaitļiem. Izrādās, ka dotajā piemērā l ir aptuveni vienāds ar 0,3010, un šo 2 bāzes 10 logaritma tuvinājumu var atrast decimālo logaritmu četrciparu tabulās. 10 bāzes logaritmi (vai 10 bāzes logaritmi) tiek tik bieži izmantoti aprēķinos, ka tos sauc parasts logaritmus un rakstīts kā log2 = 0,3010 vai log2 = 0,3010, izlaižot skaidru norādi par logaritma bāzi. Logaritmi uz bāzi e, tiek izsaukts transcendentālais skaitlis, kas aptuveni vienāds ar 2,71828 dabisks logaritmi. Tie galvenokārt atrodami darbos par matemātisko analīzi un tās pielietojumu dažādās zinātnēs. Arī naturālos logaritmus raksta, tieši nenorādot bāzi, bet izmantojot speciālo apzīmējumu ln: piemēram, ln2 = 0,6931, jo e 0,6931 = 2.

Izmantojot parasto logaritmu tabulas.

Parastais skaitļa logaritms ir eksponents, līdz kuram ir jāpalielina 10, lai iegūtu noteiktu skaitli. Tā kā 10 0 = 1, 10 1 = 10 un 10 2 = 100, mēs uzreiz iegūstam, ka log1 = 0, log10 = 1, log100 = 2 utt. veselu skaitļu pakāpju palielināšanai 10. Tāpat 10 –1 = 0,1, 10 –2 = 0,01 un tāpēc log0,1 = –1, log0,01 = –2 utt. visiem negatīvajiem veselo skaitļu pakāpēm 10. Atlikušo skaitļu parastie logaritmi ir iekļauti starp 10 tuvāko veselo skaitļu pakāpju logaritmiem; log2 ir jābūt no 0 līdz 1, log20 ir jābūt no 1 līdz 2, un log0.2 jābūt no -1 līdz 0. Tādējādi logaritms sastāv no divām daļām, vesela skaitļa un decimāldaļas, kas ir ietvertas starp 0 un 1. izsaukta vesela skaitļa daļa raksturīgs logaritmu un nosaka pats skaitlis, tiek izsaukta daļēja daļa mantisa un to var atrast no tabulām. Arī log20 = log(2ґ10) = log2 + log10 = (log2) + 1. Logaritms 2 ir 0,3010, tātad log20 = 0,3010 + 1 = 1,3010. Līdzīgi log0.2 = log(2о10) = log2 – log10 = (log2) – 1 = 0.3010 – 1. Pēc atņemšanas iegūstam log0.2 = – 0.6990. Tomēr ērtāk ir attēlot log0.2 kā 0.3010 – 1 vai kā 9.3010 – 10; Var formulēt arī vispārīgu noteikumu: visiem skaitļiem, kas iegūti no dotā skaitļa, reizinot ar pakāpju 10, ir identiskas mantisas, kas vienādas ar dotā skaitļa mantisu. Lielākajā daļā tabulu ir norādītas skaitļu mantisas diapazonā no 1 līdz 10, jo visu pārējo skaitļu mantisas var iegūt no tabulā norādītajiem.

Lielākajā daļā tabulu logaritmi ir norādīti ar četrām vai piecām zīmēm aiz komata, lai gan ir septiņu ciparu tabulas un tabulas ar vēl vairāk zīmēm aiz komata. Vienkāršākais veids, kā iemācīties izmantot šādas tabulas, ir ar piemēriem. Lai atrastu log3.59, vispirms jāņem vērā, ka skaitlis 3.59 ir no 10 0 līdz 10 1, tātad tā raksturlielums ir 0. Tabulā atrodam skaitli 35 (kreisajā pusē) un virzāmies pa rindu uz kolonnu, kuras augšpusē ir skaitlis 9 ; šīs kolonnas un 35. rindas krustpunkts ir 5551, tātad log3,59 = 0,5551. Lai atrastu skaitļa mantisu ar četriem zīmīgajiem cipariem, jāizmanto interpolācija. Dažās tabulās interpolāciju atvieglo proporcijas, kas norādītas pēdējās deviņās kolonnās katras tabulu lapas labajā pusē. Tagad atradīsim log736.4; skaitlis 736.4 atrodas starp 10 2 un 10 3, tāpēc tā logaritma raksturlielums ir 2. Tabulā atrodam rindu, no kuras pa kreisi ir 73 un kolonnu 6. Šīs rindas un šīs kolonnas krustpunktā ir skaitlis 8669. Starp lineārajām daļām atrodam 4. kolonnu 73. rindas un 4. ailes krustpunktā ir skaitlis 2. Saskaitot 2 ar 8669, iegūstam mantisu – tā ir vienāda ar 8671. Tādējādi log736.4 = 2,8671.

Dabiskie logaritmi.

Dabisko logaritmu tabulas un īpašības ir līdzīgas parasto logaritmu tabulām un īpašībām. Galvenā atšķirība starp abiem ir tāda, ka naturālā logaritma veselā skaitļa daļai nav nozīmes decimālpunkta pozīcijas noteikšanā, un tāpēc atšķirībai starp mantisu un raksturlielumu nav īpašas nozīmes. Skaitļu naturālie logaritmi 5,432; 54,32 un 543,2 ir attiecīgi vienādi ar 1,6923; 3,9949 un 6,2975. Saikne starp šiem logaritmiem kļūs acīmredzama, ja ņemsim vērā atšķirības starp tiem: log543.2 – log54.32 = 6.2975 – 3.9949 = 2.3026; pēdējais skaitlis ir nekas cits kā skaitļa 10 naturālais logaritms (rakstīts šādi: ln10); log543.2 – log5.432 = 4.6052; pēdējais cipars ir 2ln10. Bet 543,2 = 10ґ54,32 = 10 2ґ5,432. Tādējādi pēc dotā skaitļa naturālā logaritma a jūs varat atrast skaitļu naturālos logaritmus, kas vienādi ar skaitļa reizinājumiem a jebkuram grādam n skaitļi 10 ja uz ln a pievieno ln10, kas reizināts ar n, t.i. ln( aґ10n) = žurnāls a + n ln10 = ln a + 2,3026n. Piemēram, ln0,005432 = ln(5,432ґ10 –3) = ln5,432 – 3ln10 = 1,6923 – (3ґ2,3026) = – 5,2155. Tāpēc naturālo logaritmu tabulas, tāpat kā parasto logaritmu tabulas, parasti satur tikai skaitļu logaritmus no 1 līdz 10. Naturālo logaritmu sistēmā var runāt par antilogaritmiem, bet biežāk runā par eksponenciālu funkciju vai eksponentu. Ja x= baļķis y, Tas y = e x, Un y sauc par eksponentu x(tipogrāfiskas ērtības labad viņi bieži raksta y= exp x). Eksponents spēlē skaitļa antilogaritma lomu x.

Izmantojot decimālo un naturālo logaritmu tabulas, varat izveidot logaritmu tabulas ar jebkuru bāzi, izņemot 10 un e. Ja log ba = x, Tas b x = a, un tāpēc piesakieties c b x=log c a vai xžurnāls c b=log c a, vai x=log c a/log c b=log ba. Tāpēc, izmantojot šo inversijas formulu no bāzes logaritma tabulas c Jūs varat veidot logaritmu tabulas jebkurā citā bāzē b. Reizinātājs 1/log c b sauca pārejas modulis no pamatnes c uz bāzi b. Nekas neliedz, piemēram, izmantot inversijas formulu vai pāriet no vienas logaritmu sistēmas uz citu, atrast naturālos logaritmus no parasto logaritmu tabulas vai veikt apgriezto pāreju. Piemēram, log105.432 = log e 5,432/log e 10 = 1,6923/2,3026 = 1,6923ґ0,4343 = 0,7350. Skaitlis 0,4343, ar kuru jāreizina dotā skaitļa naturālais logaritms, lai iegūtu parasto logaritmu, ir modulis pārejai uz parasto logaritmu sistēmu.

Īpaši galdi.

Logaritmi sākotnēji tika izgudroti tā, lai, izmantojot to īpašības, reģistrētos ab=log a+ baļķis b un žurnālu a/b=log a– žurnāls b, pārvērst produktus par summām un koeficientus par atšķirībām. Citiem vārdiem sakot, ja log a un žurnālu b ir zināmi, tad, izmantojot saskaitīšanu un atņemšanu, mēs varam viegli atrast reizinājuma logaritmu un koeficientu. Tomēr astronomijā bieži tiek dotas log vērtības a un žurnālu b jāatrod žurnāls ( a + b) vai žurnāls( a – b). Protams, vispirms varēja atrast no logaritmu tabulām a Un b, tad veic norādīto saskaitīšanu vai atņemšanu un, atkal atsaucoties uz tabulām, atrod vajadzīgos logaritmus, taču šādai procedūrai būtu jāatsaucas uz tabulām trīs reizes. Z. Leonelli 1802. gadā publicēja tabulas t.s. Gausa logaritmi– logaritmi summu un starpību saskaitīšanai – kas ļāva aprobežoties ar vienu pieeju tabulām.

1624. gadā I. Keplers ierosināja proporcionālo logaritmu tabulas, t.i. skaitļu logaritmi a/x, Kur a– kāda pozitīva nemainīga vērtība. Šīs tabulas galvenokārt izmanto astronomi un navigatori.

Proporcionālie logaritmi plkst a= 1 tiek izsaukti kologaritmi un tiek izmantoti aprēķinos, kad jātiek galā ar produktiem un koeficientiem. Skaitļa kologaritms n vienāds ar apgrieztā skaitļa logaritmu; tie. colog n= log1/ n= – žurnāls n. Ja log2 = 0,3010, tad colog2 = – 0,3010 = 0,6990 – 1. Kologaritmu izmantošanas priekšrocība ir tāda, ka, aprēķinot logaritma vērtību tādām izteiksmēm kā pq/r pozitīvo decimāldaļu žurnāla trīskāršā summa lpp+ baļķis q+kologs r ir vieglāk atrast nekā jauktās summas un starpības žurnāls lpp+ baļķis q– žurnāls r.

Stāsts.

Princips, kas ir jebkuras logaritmu sistēmas pamatā, ir zināms ļoti ilgu laiku, un to var izsekot senajā Babilonijas matemātikā (apmēram 2000. gadā pirms mūsu ēras). Tajos laikos, lai aprēķinātu saliktos procentus, tika izmantota interpolācija starp tabulu vērtībām ar veselu skaitļu pozitīvo veselo skaitļu pakāpēm. Daudz vēlāk Arhimēds (287–212 BC) izmantoja 108 jaudas, lai atrastu augšējo robežu smilšu graudu skaitam, kas nepieciešams, lai pilnībā aizpildītu toreiz zināmo Visumu. Arhimēds vērsa uzmanību uz eksponentu īpašību, kas ir logaritmu efektivitātes pamatā: pakāpju reizinājums atbilst eksponentu summai. Viduslaiku beigās un modernā laikmeta sākumā matemātiķi arvien vairāk sāka pievērsties ģeometriskās un aritmētiskās progresijas attiecībām. M. Stīfels savā esejā Veselo skaitļu aritmētika(1544) sniedza skaitļa 2 pozitīvo un negatīvo spēku tabulu:

Stīfels pamanīja, ka divu skaitļu summa pirmajā rindā (eksponentu rindā) ir vienāda ar divu eksponentu, kas atbilst divu atbilstošo skaitļu reizinājumam apakšējā rindā (eksponentu rindā). Saistībā ar šo tabulu Stīfels formulēja četrus noteikumus, kas ir līdzvērtīgi četriem mūsdienu likumiem darbībām ar eksponentiem vai četriem likumiem darbībām ar logaritmiem: summa augšējā rindā atbilst reizinājumam apakšējā rindā; atņemšana augšējā rindā atbilst dalīšanai apakšējā rindā; reizināšana augšējā rindā atbilst eksponenciālai kāpināšanai apakšējā rindā; sadalījums augšējā rindā atbilst sakņošanai apakšējā rindā.

Acīmredzot Stīfela likumiem līdzīgi noteikumi lika Dž.Neiperam savā darbā oficiāli ieviest pirmo logaritmu sistēmu. Apbrīnojamās logaritmu tabulas apraksts, publicēts 1614. gadā. Taču Napiera domas nodarbināja problēma par produktu konvertēšanu summās, kopš vairāk nekā desmit gadus pirms sava darba publicēšanas Napier saņēma ziņas no Dānijas, ka Tycho Brahe observatorijā viņa palīgiem ir metode, kas ļauj iespējams pārvērst produktus summās. Metode, kas tika apspriesta Napier saņemtajā ziņojumā, balstījās uz trigonometrisko formulu izmantošanu, piemēram,

tāpēc Napera tabulas galvenokārt sastāvēja no trigonometrisko funkciju logaritmiem. Lai gan bāzes jēdziens Napier piedāvātajā definīcijā nebija skaidri iekļauts, viņa sistēmā logaritmu sistēmas bāzei līdzvērtīgu lomu spēlēja skaitlis (1 – 10 –7)ґ10 7, aptuveni vienāds ar 1/ e.

Neatkarīgi no Napera un gandrīz vienlaikus ar viņu 1620. gadā J. Bürgi izgudroja un publicēja Prāgā diezgan līdzīgu logaritmu sistēmu. Aritmētiskās un ģeometriskās progresijas tabulas. Tās bija antilogaritmu tabulas pret bāzi (1 + 10 –4) ґ10 4, diezgan labs skaitļa aptuvens e.

Napera sistēmā skaitļa 10 7 logaritms tika pieņemts kā nulle, un, skaitļiem samazinoties, logaritmi pieauga. Kad G. Brigss (1561–1631) viesojās Napierā, abi vienojās, ka ērtāk būtu par bāzi izmantot skaitli 10 un uzskatīt, ka logaritms viens ir nulle. Tad, skaitļiem palielinoties, to logaritmi pieaugs. Tādējādi mēs ieguvām mūsdienu decimālo logaritmu sistēmu, kuras tabulu Brigss publicēja savā darbā Logaritmiskā aritmētika(1620). Logaritmi uz bāzi e, lai gan ne tieši tos, ko ieviesa Naper, bieži sauc par Naper. Terminus "raksturīgs" un "mantisa" ierosināja Briggs.

Pirmie logaritmi vēsturisku iemeslu dēļ izmantoja tuvinājumus skaitļiem 1/ e Un e. Nedaudz vēlāk dabisko logaritmu ideja sāka saistīt ar hiperbolas apgabalu izpēti xy= 1 (1. att.). 17. gadsimtā tika parādīts, ka apgabals, ko ierobežo šī līkne, ass x un ordinātas x= 1 un x = a(1. attēlā šis laukums ir klāts ar treknākiem un retākiem punktiem) palielinās aritmētiskā progresija, kad a pieaug eksponenciāli. Tieši šī atkarība rodas noteikumos par darbībām ar eksponentiem un logaritmiem. Tas izraisīja Naperijas logaritmu nosaukšanu par “hiperboliskajiem logaritmiem”.

Logaritmiskā funkcija.

Bija laiks, kad logaritmi tika uzskatīti tikai par aprēķina līdzekli, bet 18. gadsimtā, galvenokārt pateicoties Eilera darbam, izveidojās logaritmiskās funkcijas jēdziens. Šādas funkcijas grafiks y= baļķis x, kuras ordinātas palielinās aritmētiskajā progresijā, bet abscises palielinās ģeometriskā progresijā, ir parādīta attēlā. 2, A. Apgrieztas vai eksponenciālas funkcijas grafiks y = e x, kuras ordinātas palielinās ģeometriskajā progresijā un kuru abscises palielinās aritmētiskajā progresijā, ir parādītas attiecīgi attēlā. 2, b. (Līknes y=log x Un y = 10x pēc formas līdzīgas līknēm y= baļķis x Un y = e x.) Ir piedāvātas arī alternatīvas logaritmiskās funkcijas definīcijas, piem.

kpi ; un, līdzīgi, skaitļa -1 naturālie logaritmi ir formas (2 k + 1)pi, Kur k– vesels skaitlis. Līdzīgi apgalvojumi attiecas uz vispārējiem logaritmiem vai citām logaritmu sistēmām. Turklāt logaritmu definīciju var vispārināt, izmantojot Eilera identitātes, lai iekļautu komplekso skaitļu kompleksos logaritmus.

Alternatīvu logaritmiskās funkcijas definīciju nodrošina funkcionālā analīze. Ja f(x) – reāla skaitļa nepārtraukta funkcija x, kam ir šādas trīs īpašības: f (1) = 0, f (b) = 1, f (uv) = f (u) + f (v), Tas f(x) ir definēts kā skaitļa logaritms x balstoties uz b. Šai definīcijai ir vairākas priekšrocības salīdzinājumā ar šī raksta sākumā sniegto definīciju.

Lietojumprogrammas.

Logaritmi sākotnēji tika izmantoti tikai aprēķinu vienkāršošanai, un šī lietojumprogramma joprojām ir viena no vissvarīgākajām. Produktu, koeficientu, pakāpju un sakņu aprēķināšanu atvieglo ne tikai publicēto logaritmu tabulu plašā pieejamība, bet arī t.s. slide rule - skaitļošanas rīks, kura darbības princips ir balstīts uz logaritmu īpašībām. Lineāls ir aprīkots ar logaritmiskiem svariem, t.i. attālums no skaitļa 1 līdz jebkuram skaitlim x izvēlēts vienāds ar baļķi x; Pārbīdot vienu skalu attiecībā pret otru, ir iespējams uzzīmēt logaritmu summas vai atšķirības, kas dod iespēju tieši no skalas nolasīt atbilstošo skaitļu reizinājumus vai koeficientus. Varat arī izmantot priekšrocības, ko sniedz skaitļu attēlošana logaritmiskā formā. logaritmisks papīrs grafiku zīmēšanai (papīrs ar logaritmiskām skalām, kas uzdrukātas uz abām koordinātu asīm). Ja funkcija izpilda formas jaudas likumu y = kxn, tad tā logaritmiskais grafiks izskatās kā taisna līnija, jo žurnāls y=log k + nžurnāls x– vienādojums lineārs attiecībā pret log y un žurnālu x. Gluži pretēji, ja kādas funkcionālas atkarības logaritmiskais grafiks izskatās kā taisna līnija, tad šī atkarība ir pakāpeniska. Daļēji žurnāla papīrs (kur Y asij ir logaritmiska skala, bet x asij ir vienota skala) ir noderīgs, ja nepieciešams identificēt eksponenciālas funkcijas. Formas vienādojumi y = kb rx rodas ikreiz, kad daudzums, piemēram, iedzīvotāju skaits, radioaktīvā materiāla daudzums vai bankas atlikums, samazinās vai palielinās proporcionāli pašlaik pieejamo iedzīvotāju, radioaktīvā materiāla vai naudas daudzumam. Ja šādu atkarību uzzīmē uz daļēji logaritmiska papīra, grafiks izskatīsies kā taisna līnija.

Logaritmiskā funkcija rodas saistībā ar visdažādākajām dabas formām. Ziedi saulespuķu ziedkopās sakārtoti logaritmiskās spirālēs, gliemju čaumalas savītas Nautilus, kalnu aitu ragi un papagaiļu knābji. Visas šīs dabiskās formas var kalpot kā piemēri līknei, kas pazīstama kā logaritmiska spirāle, jo polāro koordinātu sistēmā tās vienādojums ir r = ae bq, vai ln r= baļķis a + bq. Šādu līkni apraksta kustīgs punkts, kura attālums no pola palielinās ģeometriskā progresijā, bet leņķis, ko raksturo tā rādiusa vektors, palielinās aritmētiskajā progresijā. Šādas līknes un līdz ar to arī logaritmiskās funkcijas visuresamību labi ilustrē fakts, ka tā notiek tik tālu un pilnīgi atšķirīgos apgabalos kā ekscentriskas izciļņa kontūra un dažu pret gaismu lidojošu kukaiņu trajektorija.