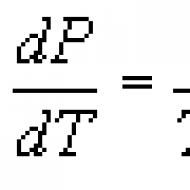クラペイロン・クラウジウス方程式。 Clapeyron 方程式と Clausius-Clapeyron 方程式 Clapeyron 方程式はどの相転移に適用できますか?
クラペイロン・クラウジウス方程式 物質がある相から別の相への転移プロセス (蒸発、融解、昇華、多形変化など) に関連する熱力学方程式。 K. - K. u. によれば、平衡過程における相転移熱 (蒸発熱、融解熱など) は次の式で求められます。 どこ た -転移温度(等温過程)、 dp/dT -特定の転移温度における温度に対する圧力の導関数の値 ( V2-V1) - 第一相から第二相への移行中の物質の体積の変化。 この方程式は、もともと 1834 年に B. P. E. Clapeyron によって、液体と熱平衡にある蒸気を凝縮させるカルノー サイクルの解析から得られたものです。 1850 年に P. Clausius は方程式を改良し、他の相転移にも拡張しました。 K. - K. u. 熱の吸収または放出を伴うあらゆる相転移 (いわゆる一次相転移) に適用でき、相平衡条件の直接的な結果です (相平衡を参照)。 ,
そこから派生したものです。 K. - K. u. 他の量が既知であれば、方程式に含まれる量のいずれかを計算するために使用できます。 特に、蒸発熱の計算に使用されますが、蒸発熱を実験的に求めるのは大きな困難を伴います。 多くの場合、K. - K. u. デリバティブを基準にして書かれています dp/dTまたは dT/dp:
蒸発および昇華プロセス用 dp/dT飽和蒸気圧の変化を表します R温度とともに Tさん溶融および多形変換プロセス用 dT/dp圧力による転移温度の変化を決定します。 つまり、K. - K. u. 変数における相平衡曲線の微分方程式です。 r、T.
K. - K. u を解くには 温度と圧力によって量がどのように変化するかを知る必要がある L、V1そして V2、それは難しい仕事です。 通常、この依存関係は経験的に確立され、K. - K. u によって解決されます。 数値的には。 K. - K. u. 純粋な物質と溶液および溶液の個々の成分の両方に適用できます。 後者の場合、K. - K. u. 特定の成分の部分飽和蒸気圧をその部分蒸発熱に関連付けます。 ユウ・I・ポリアコフ。 ソビエト大百科事典。 - M.: ソビエト百科事典.
1969-1978
.
![]()
他の辞書で「クラペイロン・クラウジウス方程式」が何であるかを見てください。
クラペイロン・メンデレーエフの式、理想気体 (理想気体を参照) の状態方程式 (状態方程式を参照)。1 モル (MOL を参照) の気体を指します。 1874年にD.I.メンデレーエフ(MENDELEEV Dmitry Ivanovichを参照)はクラペイロン方程式に基づいて…… 百科事典
クラペイロン・クローシス方程式- 物質がある相から別の相への転移プロセス (蒸発、融解、多形変化など) に関連する熱力学方程式。 Clapeyron Clausis 方程式によれば、相転移熱 (たとえば、融解熱) 冶金辞典
理想気体の状態方程式。その体積と圧力 pi abs の関係を確立します。 t roy T。形式は pV=nRT です。 ここで、n はガスのモル数、R = 8.31431 J/mol です。 K) 気体定数。 1 モルのガスの場合、pv=RT、ここで v はモル体積です。 K・M・U…… 化学事典
状態方程式 この記事は熱力学シリーズの一部です。 理想気体の状態方程式 ファンデルワールス方程式 ディテリチ方程式 熱力学の各セクション 熱力学の原理 方程式 ... Wikipedia
- (クラペイロン・メンデレーエフ方程式)、理想気体の状態を決定するパラメーター (圧力 p、体積 V、絶対温度 T) 間の関係: pV=BT、ここで係数。 比例 B はガス M の質量とそのモルに依存します。 大衆。 インストールされました… … 物理百科事典
状態方程式 Stat ... Wikipedia
- (クラペイロン・メンデレーエフ方程式)、質量 M の理想気体の圧力 p、絶対温度 T、体積 V の関係: pV=BT、B=M/m (m は原子質量での気体分子の質量)単位)。 フランスの科学者B.P.E.によって設立されました。 クラペイロン…… 現代の百科事典- クラペイロン・メンデレーエフ方程式、B. P. E. Clapeyron (1834) によって発見されました。理想気体の状態を決定する物理量間の関係、つまり気体の圧力 p、その体積 V、および絶対温度 T. K. u.... ソビエト大百科事典
クラペイロン・メンデレーエフ方程式 [フランス人の名前にちなんで命名。 物理学 B. Clapeyron (V. Clapeyron; 1799 1864) およびロシア語。 化学者 D.I. メンデレーエフ (1834 1907)]、理想気体の状態レベル: pVm = RT、p は圧力、T は気体の熱力学的温度、Vm ... ... 大百科事典ポリテクニック辞典
クラペイロン方程式とクラウジウス・クラペイロン方程式
ギブス位相則から分かるように、二相 1 成分系における独立強度変数の数は 1 に等しい。 したがって、次の関係式が存在するはずです。 Rそして テレビそういうシステム。 この関係は、位相平衡条件の結果です。
ここで、指定 p(p, た)各相の化学ポテンシャルが関数であることを強調します。 rT。
p の依存性が Rそして Tが明示的に知られている場合、(3.7) は原則として次に関して解くことができます。 Rまたは Tそして依存症を見つける R = p(T)または T = T(r)。ただし、一般的な場合、依存性 p ネガティブ 7" は不明なので実行できません。ただし、派生関数を見つけることはできます。 Rによる T(またはその逆)。
1 つの物質の 2 つの相 a と b が平衡状態にあると仮定します。 温度を値 d7" だけ変更すると、平衡条件 (3.7) に違反することなく、両方の相の化学ポテンシャルが等しく変化するように圧力が変化する必要があります。つまり、次のようになります。
両方の差分を変数に分解する ティル、我々が得る
関係 (2.31) と組み合わせると、次のようになります。
このことから、次のことがわかります。
Df Pはどこですか? - 相転移のエントロピー; A fp U=U^ -- 大臼歯
相転移体積(相転移体積によるモル体積の変化) T= 定数、 p =定数)。
相転移のエントロピーとエンタルピーは、関係式 (3.5) によって相互に関係付けられます。 AS = AN/T。したがって、(3.9) は次の形式で書くことができます。 
どこ T- 相転移温度。
式 (3.9) と (3.10) は等価であり、どちらも Clapeyron 方程式と呼ばれます。
クラペイロン方程式の実際の応用は、相転移のエンタルピーと相のモル体積が相ごとに異なるように温度に依存するという事実によって制限されます。 これは、この方程式を積分する一般的な方法がないことを意味します。 しかし、温度間隔が狭い場合は、特定の近似を受け入れることで、これらの方程式を多くの目的に十分な精度で統合できます。
最初の近似は、狭い温度範囲では相転移のエンタルピーはほぼ一定であると仮定できることです。 固体と液体の凝縮相のモル体積についても、それらは弱く依存するため、同じことができます。 ティルから。次に、固相間および固相と液相の間の相平衡については、モル体積の変化も一定であると仮定できます。 これらの近似を使用すると、(3.10) は次のように積分されます (融解の場合)。

固相間の平衡についても同様です。
気相のモル体積は一定であるとは考えられません。 ただし、低気圧の場合は、他の近似も可能です。 まず、低圧でのガスのモル体積は、凝縮相のモル体積よりもはるかに大きくなります (cf)。 したがって、蒸発のために次のものを摂取できます。
第二に、低圧では、多くのガスが
ガス CT d__ ヤット
理想に近い特性。 したがって ~-i L isp k t ~- です。
これを式 (3.10) に代入すると、次のようになります。

なぜなら &r/r= s!1p R、結果として得られる関係は、クラウジウス-クラペイロン方程式と呼ばれます。
液相と固相の両方の蒸発(昇華)に適用できます。
相転移の一定エンタルピーの近似では、この方程式は次のように積分されます。
これらの方程式を適用するには、常圧での相転移エンタルピーと相転移温度のデータがよく使用されます。 それらは、物理量および化学量の多くの参考書に記載されています。 通常の圧力は、101,325 Pa = 101.325 kPa = 1.01325 bar = 1 atm = 760 mm Hg の値です。 美術。 = 760トル。 参考書籍のデータは、通常と大きく変わらない圧力で式 (3.11) および (3.13) を使用した近似計算の基礎として機能します。
式 (3.11) を使用した計算に必要な凝縮相のモル体積は、通常、参考書には記載されていません。 しかし、それらの代わりに、河川密度に関するデータを見つけることができます。 定義を知っていれば、モル体積の計算に使用できます。 うーん = 国連、 p = それそして M = t/p.それらから次のようになります。 うーん = M/ p、ここで M -モル質量。
一方、相転移の比熱を示している参考書もあります。 この場合、式 (3.10) は次の形式で書くことができます。

ここで、Af p/g と Af P y は、それぞれ相転移中の比エンタルピーと比容積の変化です (および v= 1/r)。
気化エンタルピーが不明な場合は、ほとんどの液体の気化のモルエントロピーが約 90 J K -1 mol -1 であるという Trouton の経験則を使用して近似的に推定できる場合があります。 Dfp^ - AfpR/G であるため、L は R/J mol -1 = 90(G M/K) になります。ここで、7^ は常圧での沸点です。 この蒸発エンタルピーの値を (3.13) に代入し、 ピクセル通常の圧力は 1 気圧、温度は T! 通常の沸点 T液体上の平衡蒸気圧は次のようになります。

トラウトンの法則は、極性の高い液体、特に液体には適用されません。 関連する水やアルコールなどの液体。 (会合液体とは、分子が相互作用する液体です。 水素結合。)この規則は、沸点が約 150 ~ 1000 K の範囲内の無極性物質に適用される場合にのみ満足されます。
クラペイロン-クラウジウス方程式 (微分)。
こちらもお読みください:
|
液体-蒸気平衡曲線、つまり特定の物質の飽和蒸気圧の温度依存性は、いわゆるクラペイロン-クラウジウス方程式を解くことで求めることができます。
熱力学サイクルの方法により、この方程式の形式を確立することができます。 温度と に対応する 2 つの実験等温線があるとします (図 50)。

初期状態 1 では、1 モルの液体が温度で圧力下にあり、体積を占めます (蒸気相は存在しません)。 熱を加えることで、このモルの液体を等温的に蒸発させます。 この場合、液体には常にその飽和蒸気の圧力と等しい圧力がかかります。 その結果、液体は気体状態に変わります 2。一定の温度および圧力で 1 モルの液体を気体状態に変換するのに必要な熱量は、定義により蒸発潜熱です。 したがって、遷移 12 で液体は に等しい熱量を受け取りました。
サイクルごとに行われる仕事は、数値的には四角形 1234 の面積に等しくなります。
![]() (3.3.1)
(3.3.1)
とサイクル効率
 .
(3.3.2)
.
(3.3.2)
一方、1234 サイクルはカルノーサイクルであるため、その効率は
![]() (3.3.3)
(3.3.3)
式 (3.3.2) と (3.3.3) を比較すると、次のようになります。

 .
(3.3.4)
.
(3.3.4)
式 (3.3.4) は、少し異なる形式で表すことができます。 これを行うために、液体が状態 1 から気体状態 2 に遷移する際のエントロピーの変化を調べます (図 50)。
 ,
(3.3.5)
,
(3.3.5)
ここで、 と はそれぞれ、状態 1 の液体と状態 2 の蒸気のエントロピーです。 最後の関係を使用すると、方程式 (3.3.4) は次のように書くことができます。
 .
(3.3.6)
.
(3.3.6)
微分方程式 (3.3.4) は、クラペイロン・クラウジウス方程式です。 この式は、温度が によって変化するときの飽和蒸気圧の変化を表します。 この方程式の解を見つけるには、蒸発潜熱の温度依存性と、液体と気体の体積の温度と圧力依存性を知る必要があります。 一般に、この方程式は非線形微分方程式であり、その解は数値積分によって求められます。
臨界温度よりも大幅に低い温度では、液体が占める体積は液体が占める体積よりもはるかに小さくなります。 したがって、たとえば、水蒸気の体積は水の体積より 1600 倍大きく、温度 – ℃ で液体酸素が沸騰すると、体積は約 300 倍増加します。 したがって、温度では、方程式 (3.3.4) は次の形式になります。
. (3.3.7)
同じ近似で、飽和蒸気も理想気体とみなすことができます。 これにより、式 (3.3.7) を次のように書くことができます。
. (3.3.8)
式 (3.3.8) の左辺を から の範囲で積分し、右辺を から の範囲で積分すると、次のようになります。
 ,
(3.3.9)
,
(3.3.9)
ここで、 はその温度での実験から得られた飽和蒸気圧、 は温度範囲にわたる蒸発熱の平均値です。
式 (3.3.9) から、飽和蒸気の圧力は温度の上昇とともに指数関数的に増加することが明らかです。
クラペイロン・クラウジウス方程式は次のように書き直されました。
 , (3.3.10)
, (3.3.10)
後で示すように、液体の沸点の外部圧力への依存性も決定します。 式(3.3.10)において
は外部圧力が によって変化したときの沸点の変化です。 したがって、液体と蒸気の平衡曲線は沸騰曲線とも呼ばれます。
52. ファンデルワールス方程式 - 非理想気体の状態方程式。 ファンデルワールス方程式定数の実験による決定。
前に述べたように、低温高圧では、物質 1 モルに対するメンデレーエフ・クラペイロン方程式は次のようになります。
実験的に測定された値から大幅な偏差が生じます。
物質のすべての状態ではないにしても、少なくとも気体と液体をカバーできる、実際の物質の状態方程式を見つけるために多くの試みが行われてきました。 提案された多くの方程式の中で、最も有名なものはファン デル ワールス方程式です。
 ,
(3.4.2)
,
(3.4.2)
物質1モルについて書かれています。 モルの場合、この式は次のようになります。
 .
(3.4.3)
.
(3.4.3)
定数は実験的に決定され、分子の種類ごとに異なる値を持ちます。 式 (3.4.2) は導出されたものではなく、既知のメンデレーエフ-クラペイロン方程式に 2 つの補正を導入することによって確立されます。 これらの導入を正当化するために、式 (3.4.2) では体積が 1 モルのガスを含む容器の体積を意味することに注意してください。 物質点で構成される理想気体の場合、この体積全体が分子の移動に利用できます。 実際の気体では、分子自体が容器の体積の特定の部分を占めており、この部分には他のすべての分子がアクセスできません。 ボリュームのこの部分をボリュームから差し引く必要があります。 この場合、式 (3.4.2) は次の形式になります。
. (3.4.4)
最後の式から、補正が無限高圧で気体が占める体積に等しいことは明らかです。つまり、無限高圧でも、実際の気体の分子は互いに距離がゼロに近づくことはできません。 したがって、補正を導入するとは、分子間の反発力を近似的に考慮することになる。
ご存知のとおり、分子間には反発力だけでなく引力も作用します。 容器の壁の近くにある分子は正味の引力を受けます。
引力の作用範囲にある分子の側から見たものです(図51)。

壁面のプラットフォームを選択しましょう。 その上に分子があるとしましょう。 その結果、ガスからこの領域の分子に作用する力が生じます。
 ,
(3.4.6)
,
(3.4.6)
なぜなら、対称性の条件から、すべての力は同じ大きさと方向をもつからです。 力を面積で割ると、壁にある分子が気体の残りの部分に作用する、いわゆる分子圧力が得られます。
. (3.4.7)
式 (3.4.7) の各係数は明らかにガスの密度に比例し、密度はガスの体積に反比例するため、次のように書くことができます。
, (3.4.8)
どこ ある– 正の定数係数。
したがって、引力の作用の結果として、ガス側から壁にかかる圧力は、分子間に引力がない場合、つまり分子間に引力が存在しない場合に壁が受ける圧力 (3.4.4) よりも小さくなります。
![]() .
.
ファンデルワールス方程式はどこにありますか:
 .
(3.4.9)
.
(3.4.9)
式(3.4.9)における追加圧力の様子を説明しましょう。 ガスを無重力ピストンの下のシリンダー内に入れます。 外部圧力はガスを圧縮する、つまり分子を近づける傾向があります。 気体分子が互いに引き付け合わなければ、気体は外部圧力のみを受けます。 しかし、私たちが発見したように、分子の相互引力は分子を互いに近づける傾向もあり、外圧と同じ方向に作用します。 したがって、分子の引力の結果は、あたかもピストンの圧力に追加の圧力が加えられたかのように、ガスに対する外部圧力の見かけの増加に反映されます。
ファンデルワールス方程式定数の実験による決定
定数の実験的決定用 ある研究対象のガスは、圧力計が組み込まれた密閉容器に入れられ、このガスの圧力がさまざまな温度で測定されます。 実験的に得られた曲線を数値微分することにより、偏導関数を決定します。 ファンデルワールス方程式から、次の導関数を求めます。
 .
(3.5.1)
.
(3.5.1)
ここから値を取得します。
. (3.5.2)
式 (3.5.2) をファンデルワールス方程式 (3.4.9) に代入して、別の量を計算します。 ある:
![]() .
(3.5.3)
.
(3.5.3)
経験が示している価値観は、 あると は定数ではなく、弱いとはいえ温度に依存します。 ファンデルワールス方程式を用いた計算では定数として ある対象の温度範囲における関数の平均値を取得します


53. ファンデルワールス方程式の等温線と実験等温線との比較。 VdW 方程式からの物質の臨界パラメータの決定。 物質の準安定状態は過飽和水蒸気と過熱液体です。 ウィルソンチャンバーとバブルチャンバー。
図では、 図52は、ファンデルワールスガス等温線を示す。
非常に高温では、双曲線に近い形状になります。 これらの等温線は、物質の気体状態 (ほぼ理想気体) を特徴付けます。 温度が低下すると等温線の形状が変化し、特定の温度 (臨界) で曲線の変曲点が検出されます。 さらに低い温度 (臨界未満) では、液体-蒸気相転移に対応する水平断面の代わりに、等温線は波状の断面を持ちます (図 53)。


米。 52Rとp. 53
測定の結果、実際の物質の等温線は、セクション (気体状態) および (液体状態) のファンデルワールス等温線と実質的に一致することがわかりました。 しかしながら、中間部分では、液体−蒸気相転移に対応する水平セクション51の代わりに、ファンデルワールス等温線は波状セクションを有する。 この波状部分には次のような特徴があります。 セクション 12 は蒸気の準安定状態 (過飽和蒸気) に対応し、セクション 54 は液体の準安定状態 (過熱液体) に対応します。 ポイント 1 には飽和蒸気のみが存在し、ポイント 5 には沸騰した液体のみが存在します。 波曲線のセクション 234 に関しては、一定の温度で体積の増加が圧力の増加を引き起こす物質は自然界には存在しないため、物理的に不可能です。 後者は、この領域の温度が一定でない場合にのみ可能です。 過飽和蒸気 (セクション 12) は、圧力が以下の物質の気体状態です。 p所定の温度における飽和蒸気圧よりも高い圧力 - 純粋なガスを飽和蒸気圧よりも高い圧力まで圧縮することによって実験的に得ることができ、それは凝縮しません。 過飽和蒸気の状態は、ある程度の安定性はありますが、二相状態 (等圧線 135) よりも不安定です。ご存知のとおり、物質の一部は液体の状態であり、一部は液体の状態です。飽和蒸気の形。 そのため、わずかな外部影響で過飽和蒸気の一部が液体となり、残りの蒸気は飽和状態となります。
過熱液体(セクション 45) - 所定の温度で飽和蒸気圧よりも低い圧力で存在するという事実を特徴とする状態 - は、純粋な液体を長時間沸騰させることによって得ることができ、その結果として気泡(液体の核)が発生します。蒸発)を液体から除去し、液体を所定の圧力で沸点以上の温度まで加熱します。 過熱液体の状態は、液体と飽和蒸気の間の平衡状態よりも不安定であることもわかります。 このような過熱液体に異物の粒子が混入すると、液体は急速に二相状態に移行します。
過飽和水蒸気と過熱液体の状態は、原子核物理装置 (霧箱や気泡室) で素粒子のパラメーターを記録および測定するために使用されます。
ファンデルワールス等温線において波状部分が水平な直線135に置き換えられると、このようにして得られた等温線は物質の二相状態を定性的に正確に表すことになる。 この線の位置は、クラウジウス表記 (2.13.7) の熱力学第 2 法則を可逆閉サイクル 1234531 に適用すると決定できます。
. (3.6.1)
経路 1234531 全体に沿って物質の温度は変化しないため (この経路は同じ等温線の 2 つの可能な変形のセクションで構成されているため)、最後の方程式は次の形式で書くことができます。
. (3.6.5) と実験データは、この値が得られるファン デル ワールス方程式が近似的であることを示していますが、物質の状態変化の定性的イメージはこの方程式によって非常に正確に伝えられています。 より正確な物質の状態方程式を取得しようとする試みは数多く行われています。 しかし、これらの方程式には、ファンデルワールス方程式と同様に、物理的意味が不明瞭な補正係数が多数含まれています。
最も一般的な形式では、統計物理学の方法を使用して、学者の N. N. ボゴリュボフが状態方程式を取得しました。
 ,
(3.6.12)
,
(3.6.12)
ここで、 は温度のみの関数である、いわゆるビリアル係数です。 ボゴリュボフ方程式から、かなり正確な結果を得るには、モル体積の値が大きいほど、考慮すべき級数の項の数が少なくなることがわかります。 べき級数のすべての項が消滅し、方程式 (3.6.12) が の形をとるとき、つまり、予想どおり、ボゴリュボフ方程式はメンデレーエフ-クラペイロン方程式に変わります。 ビリアル係数は純粋に理論的な方法では計算できないため、実験データを使用して決定する必要があります。 ただし、この問題は非常に複雑であることが判明したため、実験データを記述する補間式の形式で単純に状態方程式を取得する方が適切であることが判明しました。
液体の蒸発熱の測定
液体と蒸気の間の平衡については、クラペイロン-クラウジウス方程式を次のように導出できます。
熱力学の第 2 法則によれば、システムが平衡状態にある場合、与えられた条件下では ( R、T) 仕事は何も行われていません
AP = 0; G そして -G P = 0; G そして =G P (2)
つまり、純粋な液体とその蒸気のギブズ自由エネルギーは等しい (これらは平衡状態です)。
平衡を決定する条件の 1 つ、たとえば温度を変更してみましょう (つまり、システムを次の方法で加熱します)。 T)、この結果として、新しい圧力、新しい液体と蒸気の平衡が確立されます。
G " そして =G " P (3)
または G そして = G P (4)
外部パラメータの変化が極微量で発生した場合 - dTの場合、等圧等温ポテンシャルは微小な値だけ変化します。
dG そして =dG P (5)
等圧等温ポテンシャルはシステムの自由エネルギーを表し、圧力と温度の関数です。
dG=VdP–SDT(6)
したがって、飽和蒸気圧と温度の間の定量的な関係を確立するために使用できます。
(6) を (5) に代入すると、平衡状態になります。
V そして dP-S そして dT = V P dP-S P dT(7)
どこから(8)
どこ ( S P -S そして) そして ( V P -V そして) - 物質が液体から蒸気状態に遷移する際の系のエントロピーと体積のそれぞれの変化。 熱力学の第 2 法則によれば、蒸発中の系のエントロピーの変化は蒸発熱の減少に等しい
 (9)
(9)
式 (9) を (8) に代入すると、次のようになります。
 (10)
(10)
ここで、Δ H ISPとΔ V ISP- それぞれ、蒸発中のエンタルピーと体積の変化、および T ベール- 沸騰温度。
式(10) クラペイロン・クラウジウス方程式と呼ばれる 。 (10) によれば、水の状態図 (図 1) の線の傾きは微分の符号によって決まります。 dP/dTまたはその逆数 dT/dP- 圧力の増加に伴う温度の変化を特徴づけます。
相転移のうち、蒸発と融解を考えます。 蒸発熱(液相から気相への転移)は正の熱です。 モル蒸発熱 液体物質 1 モルを蒸発させるのに消費される熱量です。 蒸発中のガスの体積は、対応する液体の体積よりも常に大きくなります。つまり、式 (10) V P >V そして。 それが理由です dP/dT、 したがって dT/dP常にプラスです ( dT/dP>0)。 したがって、蒸発温度は圧力の増加とともに常に増加します (曲線 わかりました図の 1 または表を参照してください。 1 付録)。 温度が上昇すると、液体上の飽和蒸気圧が増加し、臨界温度で最大値に達します。 後者は、物質の液相と蒸気相の間の平衡が可能な限界温度 (たとえば、水の場合は 374.12 ℃) です。 より高い温度では、物質は気体状態のみになり、飽和蒸気の概念は意味を失います。
固相から液相への転移である融解熱も常に正です。

米。 1. 低圧における水の状態の図
領域: 1 - 固相 (氷)。 II-液体; III - パー。
カーブ: AO - 昇華。 OK - 蒸発; OV - 溶ける。
Oは三相の平衡に対応する三重点です。
一般に、液相の体積は、同量の固相の体積よりも大きくなる場合も小さくなる場合もあります。 ここから、式 (10) に従って、値は次のようになります。 dP/dTまたはその逆数値 dT/dP、正または負の値を指定できます。 これは、圧力の増加に伴って融点が上昇または下降する可能性があることを意味します。 マグニチュード dT/dPほとんどの物質に対して陽性です。 これは、融点における液体の密度が固相の密度より大きい、水、ビスマス、およびその他のいくつかの物質に対してのみ負の値を持ちます ( V そして -V T) < 0. В связи с этим при увеличении давления температура плавления льда понижается (криваяOB).
考慮されたパターンは低圧力に対して有効であることに注意してください。
Clapeyron-Clausius 方程式 (10) は、次の近似を行うことで変形できます。
1) Δ以降 V ISP =(V P -V そして) >> 0 (たとえば、水の場合、蒸気状態のモル体積は 0 です。 V P≈ 22400 cm 2、液体状態 V そして≈ 18 cm 3)、大きな誤差がなければ、この値は無視できます。 V そしてそしてそのΔを受け入れます V ISP ≈ V P .
2) 圧力と温度が高すぎない (臨界からはほど遠い) 場合、理想気体の状態方程式は実際のシステムに適用できます。 この場合に得られる誤差は、重要ではないことがわかります。
 (11)
(11)
(11) を (10) に代入すると、次のようになります。
 (12)
(12)
変身後はどれ
 (13)
(13)
形をとる
 (14)
(14)
気化熱は温度に依存します :温度が上昇すると気化熱は減少します。 臨界温度では、蒸発熱はゼロになります。 ただし、臨界から程遠い温度では、Δの変化は N ISP温度に関してはあまり良くありません。 広すぎない温度範囲でΔ N ISP一定であると考えることができます。
温度範囲内での Clapeyron-Clausius 方程式 (14) の積分 T 1と T 2、圧力に対応 R 1と R定数Δで2 N ISP、与える
 (15)
(15)
または 10 進対数に移動する場合
 (16)
(16)
(R- 8.314 J/mol K に等しい普遍気体定数)。
式 (15)、(16) により、蒸発熱を計算できます。 これを行うには、実験データに基づいて依存関係を構築します。 私nP=f(1/T) または lgP=f(1/T) を選択し、得られた直線上の 2 点を選択します (図 2)。 これらの点に対応する圧力の対数と温度の逆数の値を式 (17) に代入します。
 (17)
(17)
Δ値 N ISP式 (17) によると、取得した温度間隔に依存し、真の温度間隔に近づくほど、この間隔は小さくなります。 ただし、そのような計算には、沸点と蒸気圧の非常に正確な測定が必要です。
Δを計算するには N ISP比較的広い温度範囲 (50 ~ 100 ℃) では、直線に最も正確に適合する点を選択する必要があります。 lgP=f(1/T).
液体の沸点、特定の温度での蒸気圧、気化熱 物質の特定の定数です 、その値は多くの理論的および実際的な計算に必要です。 これらのデータに基づいて、化学物質の純度を決定し、蒸留による混合物の分離を計算し、気相での反応を実行するために必要な液体の蒸発にかかるエネルギーコストを計算することができます。
分子パラメータを使用して蒸発熱を計算するには、常に仮定が必要です。 これはおおよその値であり、いくつかの条件が満たされる場合に適しています。 ただし、蒸発熱とシステムの他の熱力学特性を結び付ける基本的なクラペイロン-クラウジウス方程式があり、厳密に熱力学第 2 法則に基づいて得られます。
カルノーサイクルを実行する作動物質を二相液体飽和蒸気系とする。 このようなシステムの初期状態を図 8.17 のポイント 1 として示します。 ある温度で状態 1 から状態 2 まで系の等圧等温膨張を実行してみましょう。この場合、一定質量の液体が蒸発し、したがって液体の蒸発熱に等しい熱が吸収されます。サーモスタットから。 点 2 と点 1 の体積の差は、物質の蒸発質量の気体状態と液体状態の体積の差に等しくなります。二相系は、状態 2 から、より低い温度の状態 3 に断熱的に移行します。 7%。 状態 3 から、作動物質は等圧等温的に状態 4 に移行し、蒸気の一部が凝縮して熱が冷凍機に放出されます。状態 4 から、二相系は断熱圧縮によって初期状態に移行します。 サイクルワークは次のとおりです。
サイクル効率はどこにありますか
![]()
温度 (圧力) 差が小さい場合、サイクル仕事量は次のようになります。
(83.3) と (83.2) を使用して、(83.1) を書き換えます。
![]()
置き換えて限界まで渡すと、次のようになります。
![]()
この関係は、熱力学の第一法則が確立される前に、フランスの技術者クラペイロン (1832 年) によって発見されました。

この方程式の現代的な導出はクラウジウスによって与えられたため、クラペイロン-クラウジウス方程式と呼ばれています。 この式を使用すると、飽和蒸気圧の温度依存性と、液体と蒸気の体積 (比、モル) がわかっている場合、蒸発熱 (比、モル) を計算できます。
導関数は、実験的に見出された依存性(飽和蒸気圧の温度依存性)から決定されます。
クラペイロン-クラウジウス方程式は、液体-蒸気転移だけでなく、他のすべての相転移にも当てはまります。 相が温度変化と平衡状態になる圧力の変化を表します。 したがって、溶融の場合、式 (83.4) は次の形式になります。
![]()