St.の配電線。 離散確率変数の分布の法則。 問題解決の例 離散確率変数の指定方法

「かわいらしいヒロインが逃亡中に、曲がりくねった危険な山道に出くわすことは十分に認めます。 彼女が足を踏み入れた瞬間に、深淵に架かる橋が崩壊する可能性は低いですが、それでも可能性はあります. 彼女が最後の瞬間に草の葉をつかんで深淵にぶら下がる可能性は非常に低いですが、そのような可能性があっても私は同意できます. かなり難しいですが、その時ちょうどハンサムなカウボーイが通りかかって不幸な人を助けてくれると信じられます。 しかし、その瞬間、カメラを持ったカメラマンがいて、これらすべてのエキサイティングなイベントをフィルムでキャプチャする準備ができているでしょう-私はこれを信じられません、ありがとう!

カウボーイ西部劇のニールス・ボーア

確率論の中心的な概念の 1 つは、確率変数の概念です。

ランダム値- これは、テストの結果として、事前に未知であり、事前に考慮できないランダムな原因に応じて、唯一の可能な値をとる量です。

ラテンアルファベットの文字で確率変数を示します バツ, よ, Z

確率変数は次のとおりです。

離散

連続

混合（離散-
連続）

例：サイコロ。 ドロップされた数は、1、2、3、4、5、または 6 のいずれかの値を同じ確率で取ることができる確率変数です*。

例：生徒の身長 - 生徒の身長は、1 m から 2.5 m までの数値範囲の任意の値を取ることができ、可能な値の数は無限です。

離散確率変数の分布法則

離散確率変数を指定するには、考えられるすべての値をリストするだけでは十分ではなく、それらの確率も示す必要があります。

離散確率変数の分布法則確率変数の可能な値とそれらの発生確率の間の対応と呼ばれます。

分布法則は、分析的に (式の形式で) 表で、またはグラフで (分布多角形の形式で) 指定できます。

確率変数を考える バツ、値を取ります ×1, x2, ×3 . × nある程度の確率で 円周率 、 どこ 私= 1..n. 確率の合計 円周率 1に等しい。

確率変数の値とその形式の確率の対応表

と呼ばれる 離散確率変数の分布の近くまたは配布の直前。 この表は、離散確率変数を指定する最も便利な形式です。

このテーブルのグラフィカル表現は 配布ポリゴン。離散確率変数の可能な値は横軸に沿ってプロットされ、対応する確率は縦軸に沿ってプロットされます。

離散確率変数の数値特性

分布法則は、離散確率変数を完全に特徴付けます。 ただし、分布法則を決定することが不可能な場合、またはこれが必要でない場合は、確率変数の数値特性と呼ばれる値を見つけることに限定できます。

• 期待値、
• 分散、
• 標準偏差

これらの量は、確率変数の値がグループ化される平均値と、この平均値の周りの分散の程度を決定します。

数学的期待値 M離散確率変数は、確率変数の平均値であり、確率変数のすべての可能な値とその確率の積の合計に等しくなります。

数学的期待値の特性:

確率変数の多くの実際に重要な特性を説明するには、その数学的期待値だけでなく、平均値からの可能な値の偏差も知る必要があります。

確率変数の分散- 確率変数の広がりの尺度。確率変数の数学的期待値からの偏差の二乗の数学的期待値に等しい。

数学的期待値の特性を考慮すると、次のことを簡単に示すことができます。

確率変数の数学的期待値からの二乗偏差ではなく、単に偏差を考慮するのが自然に思えます。 ただし、この偏差の数学的な期待値はゼロです。 これは、考えられる偏差のいくつかは正であり、他の偏差は負であり、それらの相互の相殺の結果としてゼロが得られるという事実によって説明されます。 分散の尺度として、確率変数の数学的期待値からの偏差係数の数学的期待値を取ることができますが、原則として、絶対値に関連するアクションは面倒な計算につながります。

分散特性:

1. 定数の分散はゼロです。
2. 定数係数は、それを二乗することによって分散符号から取り出すことができます。
3. もし バツ と y 独立確率変数の場合、これらの変数の合計の分散はそれらの分散の合計に等しくなります。

標準偏差確率変数 (時には " 確率変数の標準偏差 "") に等しい数と呼ばれます

したがって、標準偏差は、分散と同様に分布の分散の尺度ですが、分散とは異なり、確率変数の値を測定するために使用されるのと同じ単位で測定されます。

テストの繰り返し。 ベルヌーイの公式。

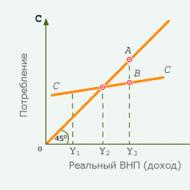
ランダムにコインを投げて上下逆さまになる確率は1/2です。 では、イベントの発生確率がわかれば、コインを 100 回投げると紋章が 50 回出現すると予測できますか? 正確に 50 である必要はありません。しかし、そのあたりは確かです。

Jacob Bernoulli (1654-1705) は、イベントが発生する確率が しかし正確に来る k独立時 nテストは





どこ p- イベントが発生する確率 しかし, q逆の事象が起こる確率です。

flash-library.narod.ru

離散確率変数の指定方法 736

その他の関連資料:

離散確率変数に関心があるとします バツ. それを完全に説明するには、可能なすべての値を示すだけで十分です。 バツ 1 , バツ 2 , . × n（ここ nは与えられた整数) と確率 R X= 私は>= 私は、 どこ 私 = 1, 2, . nこれらの値が受け入れられるもの。 通常、これらすべての値は表の形式で記録されます (表 3.1)。

この表は、離散確率変数の分布法則と呼ばれます (統計と確率論の関係を確認するには、離散統計機能の変動系列と比較してください)。

この一連の条件の実装ごとに、確率変数 バツ可能な値のセットから 1 つの値のみを取得できる場合、これらの値は互換性のないイベントの完全なグループを表します。 次に、確率の加算の規則からの系 2 に基づいて、条件を満たす必要があります。 これを正規化条件と呼びます。

グラフィカルに、離散確率変数の分布法則は破線、つまり多角形として表すことができます (図 3.2) (ここでも、変分級数を思い出すことが適切です)。



米。 3.2. 分配法則のグラフ表示
離散確率変数

離散確率変数の可能な値のセットが無限であるが可算である場合、分布法則は次の形式になります (表 3.2)。

講義 1_06: 確率論。 ランダム変数

確率論の実際の使用では、素事象の空間は扱われません。 この概念は、確率論的スキームの理論的実証に必要です。 イベントが特定の数の出現であるランダムスキームが最も頻繁に考慮されます。 このようなスキームでは、確率変数の概念が導入されています。 この概念は、私たちの講義の焦点になります。 確率変数、それらを指定する方法 (いわゆる分布法則)、確率変数の数値特性、および最も一般的な分布法則について検討します。

確率変数は、基本イベントのセットを実数 (または整数) のセットにマッピングしたものです。

次のスキームが想定されます。ランダムな実験の結果として、基本イベントの1つが選択され、そこから関数の値が計算され、この値が観察されます。 前述のマッピングは、確率変数の特定の値の発生確率を決定します。

たとえば、基本イベントのセットがサイコロを 2 回投げることで構成されているとします。これにより、36 の基本的な結果が得られます。 関数 ξ を、サイコロを振った値の合計として定義します。 明らかに、そのような確率変数は2から12までの値をとることができます。この場合、値2は1つの基本イベントに対応し、たとえば、値9 - 4：(3.6)、(4.5)、(5.4)および ( 6.3)。

通常、それは私たちが完全に知らない素的な出来事ではなく、観測され研究される確率変数です。 それらの確率的動作を設定するには、確率変数が特定の値を取る確率を設定する必要があります。 私たちが考える確率変数の例は、次のように定義できます。

さいころを 3 回振って点数の合計が出る確率の表を自分で作ってみてください。

確率変数がその値を取る確率の決定は、その分布法則と呼ばれます。

確率変数の分布関数

分布法則を設定する最も重要な方法の 1 つは、分布関数を設定することです。

確率変数 ξ の分布関数は次の関数です。

写真は示す
例として考えられる確率変数の分布関数。

わかりやすくするために、関数のグラフの下の領域は灰色でシェーディングされています。 この関数が単調に非減少であり、区分的に一定であることがはっきりとわかります。 確率が正の値に対応するポイントでジャンプします。

このような分布関数は、しばしば積分と呼ばれます。 連続で導関数がある場合、この導関数はしばしば分布密度と呼ばれます。 この例のように、分布関数が区分的に一定である場合、一連のジャンプが密度の役割を果たすことができます。

任意の分布関数を定義するのは面倒です。 簡単にするために、2 つのアプローチを使用します。

まず、確率変数のいくつかの非常に単純な数値特性に自分自身を制限できることがよくあります。

第 2 に、確率分布には複数のクラスが発生することが多く、多くの場合、何らかの「モデル」上の理由から、特定の分布がどのクラスに属しているかを理解できます。 この場合、この分布のパラメータを指定するだけで十分です。

これらのアプローチを検討していきます。

確率変数の特徴

確率変数 ξ が与えられ、有限個の値を取るとします。 a 1 , a 2 , . a k確率で
p 1 , p 2 , . p k. この確率変数の数学的期待値は合計です えξ = Σ 私約 1: k p 私 a 私 .

より一般的なケースで数学的な期待値がどのように決定されるかについては、個別に話す必要があります。積分が使用されますが、積分は積分和によって定義されることをすでに教えられており、確率変数については、それらに近い離散確率変数を導入できます。 、その数学的期待値は、元の確率変数の数学的期待値の積分和の役割を果たします。

この式からわかるように、数学的期待値は、一連の質量の重心として解釈できます。 p 私ポイントに集中 a 私. 当然、その特性は重心の特性としてよく知られています。

4. a、つまり、 k= 1 の場合 えξ = a,
5. η = cξ 、ここで c一定である場合、 えη = cえξ ,
6. 任意の ξ と η に対して、 え(ξ + η) = えξ + えη .

確率変数の分散は、この確率変数の数学的期待値からの偏差の 2 乗の数学的期待値です。

この定義は、最初は静かな恐怖を引き起こします。 実際、これは数式の非常に便利な口頭での説明です。 数学的期待という言葉は、私たちが書くべきことを意味します
Dξ = え (.)
正方形が明確になります
Dξ = え (.) 2
偏差は括弧内の式にすでに適用されています
Dξ = え (. − .) 2
数学的期待値からのランダム変数は、式の記述を完了します
Dξ = え (ξ − えξ) 2

分散は、重心の周りの同じ一連の質量の慣性モーメントとして解釈できます。 その特性もよく知られています。

7. 確率 1 の確率変数が値を取る場合 a、 それから Dξ = 0,
8. η = cξ 、ここで c一定である場合、 Dη = c 2 Dξ .
9. 平等にしたい D(ξ + η) = Dξ + Dη ですが、独立した確率変数の場合にのみ当てはまります。

ランダム変数 ξ と η は、任意の場合、独立していると呼ばれます aと b独立したイベント

まとめてみるとわかりやすい n数学的な期待値を持つ独立した同一分布の確率変数 aと分散 b、その合計の数学的期待値と分散は、それぞれ、 なしと 注意、および算術平均 - それぞれ aと b/n .

したがって、確率変数の数学的期待値である数値を評価したい場合は、確率変数を何度も観察して算術平均を計算するランダム検定を行うことができます。 真の値の周囲の広がりは、観測数の増加とともに減少します。100 回測定すると、10 分の 1 に減少します (重要なのは分散自体ではなく、その根であるため)。 この事実は、統計モデリングの重要な計算方法の根底にあります。

ランダムイベントとの類推により、相互に独立した確率変数とペアごとに独立した確率変数を区別できることに注意してください。 前述の分散の特性については、確率変数がペアで独立していれば十分です。 他の特性が使用されますが、これらは最も重要です。 ここで、いくつかの重要な種類の分布を検討し、そのたびにそれらの数学的期待値を示します。

配布タイプ

一様分布

確率変数は区間 [ a,b] 、 どこ aその分布関数の場合
ふ(バツ) は 0 に等しい バツ、1 で バツ > bで 0 から 1 まで直線的に変化します。 a .

(a + b)/2 で、分散は ( b − a) 2 /12 .

次の図は、この分布関数のプロットを示しています。 a= 0 および b = 1 .

確率変数 (疑似乱数) のすべての標準的なコンピューター センサーはまさにそのような確率変数をモデル化し、それらから必要な確率変数が作成されるため、この分布法則は私たちにとって非常に重要です。

指数分布

確率変数は、非負であり、 ふ(バツ) = 1 − exp(−λ バツ) 、ここで λ は正の定数です。

このような確率変数の数学的な期待値は λ − 1 で、分散は λ − 2 です。

次の図は、λ = 3 の場合のこの分布関数のプロットを示しています。

アプリケーション、特に無線工学と通信において、この分布法則にしばしば遭遇します。 特に、2 人の加入者の会話時間は指数法則に従って分配されると想定されることがよくあります。

正規分布

これは標準的な確率分布の中で最も人気があり、一見、このような複雑な式が最も一般的であることは奇妙に思えるかもしれません。

確率変数は正規分布またはガウス分布に従う場合 (右側は K. F. ガウス (1777-1855) の肖像)



この関数はパラメータに依存します aとσ。 このような確率変数の数学的期待値は次のとおりです。 a、分散は σ 2 です。



グラフは、 a= 0 および σ = 1 .

アプリケーションでこの法則が頻繁に現れる理由は、確率変数を追加すると、確率変数と見なされるそれらの合計の分布が非常に頻繁に正規に近づくためです。

私たちのタスクでは発生しませんが、言うまでもなく卑猥です。

ベルヌーイ分布

この最も単純な離散分布は、スイスの数学者ヤコブ・ベルヌーイ (1654-1705) にちなんで名付けられました (サンクトペテルブルクで働いていた若い方もいました)。

確率変数は、値が 2 つしかない場合、ベルヌーイ分布です。 通常、これらの値は 1 であり、その確率は p ,
そして0、その確率はに等しい q = 1 − p.

このような確率変数の数学的期待値は次のとおりです。 p、分散は pq .

もちろん、そのようなスケジュールを自分で作成します。

ベルヌーイの法則は、あらゆる種類のモデル構築に非常に便利です。特定のケース (コインを投げる場合) よりも少しだけ複雑です。 p = 1/2 .

二項分布

合計に等しい確率変数 ξ n独立同一ベルヌーイ確率変数は、二項分布を持ちます。 彼女のために

このような確率変数の数学的期待値は次のとおりです。 np、分散は npq .

項数が増加する二項分布 n正規分布に非常に似ています。

確率変数を適切な方法で正規化することだけが必要です。数学的期待値を引き、分散の根で割ります。つまり、ξ の代わりに、
η = (ξ — np)(npq) − 1/2 .

成長があれば n確率 p減少し、製品が保存または安定するような方法で np、次に説明する別の古典的な分布を取得します。

ポアソン分布

この分布は、サンクトペテルブルク科学アカデミーの名誉会員であるフランスの数学者シメオン ポアソン (1781-1840) によって提案されました。

次の場合、確率変数 ξ はポアソン分布になります。

このような確率変数の数学的期待値は λ であり、分散も λ です。



ポアソン分布は、まれなイベントのスキームの典型です。ベルヌーイ分布のランダム変数が多数あり、それぞれに肯定的な結果が生じる可能性は非常に小さいです。

たとえば、封筒にマークのないメールボックスにドロップされた手紙の数には、ポアソン分布があることが注目されています。

演習

確率変数は、0.3 の確率で 0、0.2 の確率で 2、0.5 の確率で 4 の値を取ります。 その数学的期待値と分散を見つけます。

2 つの確率変数の数学的な期待値は 0 で、分散は 1 です。合計の分散はどの程度変化しますか。 合計の分散の最大値と最小値を使用して例を作成します。

試験問題

確率変数とその分布関数。

数学的期待値と分散。 それらのプロパティ。

www.math.spbu.ru

教育ブログ - 勉強のためのすべて

実験の繰り返し

確率論の実際の応用では、同じ実験または類似の実験が複数回繰り返されるという問題に遭遇することがよくあります。 各実験の結果として、いくつかのイベント A が表示される場合と表示されない場合があり、個々の実験の結果ではなく、一連の実験の結果としてイベント A が発生した合計数に関心があります。 このような問題では、一連の実験の結果として、任意の数の事象が現れる確率を決定できる必要があります。 実験が独立している場合、それらは非常に簡単に解決されます。

いくつかの実験は、各実験のいずれかの結果の確率が他の実験の結果に依存しない場合、独立していると呼ばれます。

独立した実験は、同じまたは異なる条件下で行うことができます。 最初のケースでは、すべての実験でイベント A の確率は同じ Р i (А) = const です。 2 番目のケースでは、イベント A の確率は経験ごとに変化し、Р i (А) = var となります。 前者は特定の定理で、後者は実験の繰り返しに関する一般的な定理です。

実験の繰り返しに関する特定の定理の定式化:
n 個の独立した実験が実行され、それぞれのイベント A が確率 p で発生する場合、イベント A が正確に m 回発生する確率は次の式で表されます。

ここで、q = 1 - p、C n m はすべての組み合わせの数です。 事象 A が発生した n 回の実験から m 個を選択できる方法の数。

一般定理式:

ここで、z は任意のパラメーターです。

一般的にも特定の場合にも:

確率変数とその分布の法則
確率変数は、実験の結果として、ある値または別の値を取ることができる量であり、どの値であるかは事前にわかりません。

確率変数には次の 2 つのタイプがあります。
連続;
不連続 (離散)。

将来的には、確率変数を大文字で表し、可能な値を対応する小文字で表すことに同意しましょう。
例：
X は 3 発のヒット数です。
× 1 = 0;
× 2 = 1;
× 3 = 2;
× 4 = 3。

可能な値 x 1 、 x 2 、…、 x n を持つ不連続確率変数 X を考えてみましょう。 これらの値はそれぞれ可能ですが、確実ではなく、Xの値はある程度の確率でそれぞれを取ることができます
X \u003d x 1;
X \u003d x 2;
X \u003d x 3;
X \u003d x 4。

互換性のないイベントは完全なグループを形成するため、∑P m,n = 1 です。 この合計確率は、個々の値の間で何らかの方法で分散されます。 この分布が与えられている場合、確率変数は確率論的な観点から完全に記述されます。 各イベントの正確な確率が記載されています。 これにより、いわゆる確率変数の分布法則が確立されます。

確率変数の分布の法則確率変数の可能な値とそれに対応する確率の間の関係を確立する関係が呼び出されます。

不連続確率変数 X の分布法則は、次の形式で与えることができます。
表形式;
分析的;
グラフィック。

不連続確率変数 X の分布法則を設定する最も簡単な形式はテーブルです。

ランダム変数。 離散確率変数。
期待値

の第 2 セクション 確率論ひたむきな ランダム変数 、このトピックに関するすべての記事で、目に見えない形で文字通り私たちに同行しました。 そして、それが何であるかを明確に表現する時が来ました：

ランダム と呼ばれる 価値、テストの結果として 唯一無二のランダムな要因に依存し、事前に予測できない数値。

確率変数は通常 指定する終えた * 、および対応する下付き文字付きの小文字の値、たとえば .

* ギリシア文字と同様に使われることもある

の例に出くわしました 確率論の最初のレッスンここで、実際には次の確率変数を考慮しました。

-サイコロを投げた後に落ちるポイントの数。

このテストにより、 一つだけ予測不可能な線 (トリックは考慮されません); この場合、確率変数は次の値のいずれかを取ることができます。

- 新生児 10 人中の男の子の数。

この数が事前にわかっていないことは明らかであり、次の 10 人の子供が生まれる可能性があります。

または男の子 - 唯一無二のリストされたオプションの。

そして、体型を維持するために、少しの体育を行います。

・ジャンプ距離が長い （一部ユニット）.

スポーツの達人でさえ、それを予測することはできません🙂

しかし、あなたの仮説は何ですか？

出来るだけ早く 実数の集合無限の場合、確率変数は次の値を取ることができます 無限に多いある間隔からの値。 そして、これが前の例との根本的な違いです。

この上、 確率変数を 2 つの大きなグループに分けることをお勧めします:

1) ディスクリート （間欠）確率変数 - 個別に取得された分離された値を取ります。 これらの値の数 もちろんですまた 無限だが可算.

・・・意味不明な用語が描かれた？ 緊急に繰り返す 代数の基礎!

2) 連続確率変数 - かかる 全て有限または無限の範囲からの数値。

ノート : 省略形の DSV と NSV は、教育文献でよく使用されます。

まず、離散確率変数を分析してみましょう。 連続.

離散確率変数の分布法則

- これは 適合この量の可能な値とその確率の間。 ほとんどの場合、法律は表に書かれています。

この用語はかなり一般的です 行 分布、しかし、場合によっては曖昧に聞こえるので、「法律」を守ります。

そしていま 非常に重要なポイント: 確率変数 必要な受け入れます 値の 1 つ、次に対応するイベントフォーム フルグループそして、それらの発生確率の合計は 1 に等しくなります。

または、折りたたんで書かれている場合:

したがって、たとえば、サイコロ上のポイントの確率分布の法則は次の形式になります。

離散確率変数は「適切な」整数値しかとれないという印象を受けているかもしれません。 幻想を払拭しましょう - それらは何でもかまいません:

一部のゲームには、次の利得分配法則があります。

...おそらく、あなたはそのようなタスクを長い間夢見てきました🙂秘密を教えましょう-私もです。 特に作業終了後 場の理論.

解決: 確率変数は 3 つの値のうちの 1 つしかとれないため、対応するイベントが形成されます。 フルグループ、これは、それらの確率の合計が 1 に等しいことを意味します。

「パルチザン」を公開します。

– したがって、従来の単位を獲得する確率は 0.4 です。

コントロール: 確認する必要があるもの。

答え:

分配法則を個別に編集する必要がある場合は珍しくありません。 この用途に 確率の古典的な定義, 事象確率の乗法・加法定理その他のチップ テルベラ:

ボックスには50枚の宝くじがあり、そのうち12枚が当選し、そのうち2枚がそれぞれ1000ルーブルを獲得し、残りはそれぞれ100ルーブルを獲得します。 ボックスから 1 枚のチケットがランダムに引き出された場合の賞金のサイズである確率変数の分布の法則を作成します。

解決: お気づきのように、確率変数の値を 昇順. したがって、最小の賞金、つまりルーブルから始めます。

合計で、そのようなチケットは 50 - 12 = 38 あり、 古典精細:
ランダムに抽選されたチケットが当たらない確率です。

残りのケースは単純です。 ルーブルを獲得する確率は次のとおりです。

そしてのために：

チェック: - そして、これはそのようなタスクの特に楽しい瞬間です!

答え: 必要な利得分配法則:

独立した決定のための次のタスク:

射手が的を射る確率は です。 確率変数の分布法則を作成します - 2 ショット後のヒット数。

... 私はあなたが彼がいなくて寂しかったことを知っていました 🙂 私たちは覚えています 掛け算と足し算の定理. レッスンの最後に解決策と答え。

分布法則は確率変数を完全に説明しますが、実際には、その一部だけを知っておくと便利です (場合によってはより便利です)。 数値特性 .

離散確率変数の数学的期待値

得られた結果の確率論的意味は何ですか? 十分な回数サイコロを振ると、 平均減点は 3.5 に近くなり、テストを行うほど、より近くなります。 実は、この効果については、すでにレッスンで詳しく説明しました 統計的確率.

では、仮想ゲームを思い出してみましょう。

疑問が生じます: このゲームをプレイすることは有益ですか? …感想は？ だから「手抜き」とは言えません！ しかし、この質問は、本質的に、数学的期待値を計算することで簡単に答えることができます - 加重平均勝つ確率:

したがって、このゲームの数学的期待値は 負け.

印象を信用しないでください - 数字を信頼してください！

はい、ここでは 10 回または 20 ～ 30 回連続で勝つことができますが、長期的には必然的に台無しになります。 そして、そのようなゲームをプレイすることはお勧めしません🙂まあ、たぶん 楽しみのために.

上記のすべてから、数学的な期待値は RANDOM 値ではないことがわかります。

独立した研究のための創造的なタスク:

Mr X は次のシステムに従ってヨーロピアン ルーレットをプレイします。彼は常に赤に 100 ルーブルを賭けます。 確率変数の分配法則 - そのペイオフを構成します。 賞金の数学的期待値を計算し、コペックに切り上げます。 どのように 平均プレイヤーは 100 ベットごとに負けますか?

参照 : ヨーロピアン ルーレットには、18 個の赤、18 個の黒、および 1 個の緑のセクター (「ゼロ」) が含まれます。 「赤」が出た場合、プレーヤーにはダブルベットが支払われ、それ以外の場合はカジノの収入になります

独自の確率テーブルを作成できるルーレット システムは他にもたくさんあります。 しかしこれは、プレイヤーの数学的期待値がまったく同じであることが確実に確立されているため、分布法則やテーブルが必要ない場合です。 システムからシステムへの変更のみ 分散、レッスンのパート 2 で学習します。

ただし、その前に、電卓のキーに指を伸ばすと便利です。

確率変数は、独自の確率分布法則によって与えられます。

であることがわかっているかどうかを調べます。 チェックを実行します。

それから私たちは研究に目を向けます 離散確率変数の分散、そして可能であれば、

健康診断には何が含まれますか (命令 302n による) 命令 No. 302n に従って健康診断を実施する場合、全員が次の検査を受ける必要があります。尿の臨床分析。 […]

海外に住む同胞のロシア連邦への自発的な再定住を支援する国家プログラム国家の参加者のためのステップバイステップガイド[…]

私たちは、グループ 2 の障害者の最低年金の規模を把握し、現在、国は社会的に保護されていない人口セグメントにさまざまな方法で支援を提供しています。 特別なケア […]

危険な状況では、特定の選択肢の結果と、これらの結果が発生する可能性を知っています。 つまり、結果の確率分布がわかっているので、結果を次の形式で表す (モデル化する) ことができます。 確率変数. このセクションでは、本書の資料をさらに研究するために必要な確率変数とその決定方法に関する確率論からの情報を思い出します。

古典的な定義によれば、ランダム値とは、その値が経験ごとにランダムに変化する量です。 つまり、各「テスト」で、特定のセットから 1 つの値を取得できます。 同時に、それがどのような値になるかを予測することは不可能です。

確率変数は、離散変数と連続変数に分けられます。 離散 CV は、有限または可算の値のセットのみを取ることができます。 連続 SW は、無限の間隔を含む、閉じた間隔または開いた間隔から任意の値を取ることができます。

3.2.2. 確率変数の分布法則

確率変数は、その分布法則によって決定されます。 分配法次の場合に設定されていると見なされます。

• 確率変数（無限を含む）の可能な値のセットと
• 確率変数がこのセットの任意の領域に入る確率、またはそのような確率を計算できる法則 (式)。

実際、確率は、特定の領域で確率変数が発生する可能性を特徴付ける指標です。

確率変数のさまざまな値の確率を決定する最も一般的で一般的な方法は、設定することです 確率分布関数と略されます。 分布関数.

確率変数 X の分布関数は関数 F(x) であり、CV が特定の値 x より小さい値を取る確率を設定します。つまり、次のようになります。

F(x) = P(X< x)

X ("x big") - 確率変数を示します。

x ("x small") - 確率変数の可能な値のセットからの特定の値。

分布関数は非減少です。 x が負の無限大になる傾向がある場合、x はゼロになる傾向があり、x がプラスの無限大になる傾向がある場合、x は 1 になる傾向があります。

確率変数の分布法則の表現形式は異なる場合があり、それが離散的か連続的かによって異なります。

次の依存関係は、分布関数の定義から得られます。

確率変数が a から b までの区間で値を取る確率:

P(a ≤ X< b) = F(b) - F(a)

確率変数がa以上の値を取る確率:

3.2.3. 離散確率変数の分布を表す方法

離散確率変数分布関数または分布の行 (テーブル) によって完全に指定できます。 これらは、表形式、分析形式、またはグラフ形式で表示できます。

確率変数 X が、それぞれ 25% 、 35% 、および 40% の確率で 25 、 45 、および 50 の 3 つの可能な値を取ることができるとします。 この SW の配布シリーズは次のようになります。

特定の値を超えない確率を示す同じ確率変数の分布関数は、次のように記述できます。

図 3.1 は、この離散確率変数 X の分布法則を設定するためのグラフィカルな方法を示しています。

図3.1。

確率分布系列 p j のグラフでは、各可能な値 x j の実現がバーで表され、その高さは確率に等しくなります。 すべての M バー (つまり、すべての確率) の高さの合計は、すべての可能な x 値をカバーするため、1 に等しくなります。

場合によっては、列の代わりに破線が描かれ、CB の値を実現する確率が結ばれます。

離散確率変数が a 未満の値を取る確率は、a 未満のすべての結果の確率の合計に等しくなります。

定義により、これは点 x = a における分布関数の値に等しくなります。 xがマイナス無限大からプラス無限大までのすべての値を「実行」するときの分布関数の値を座標平面にプロットすると、分布関数のプロットが得られます。 ディスクリート SW の場合は段階的です。 負の無限大から最初の可能な値 x 1 までの区間では、この区間では値を受け入れることができないため、ゼロに等しくなります。

さらに、ｘ j の各可能な値は、この値ｐ j の発生確率に等しい量だけ分布関数を増加させる。 x j と x j+1 の 2 つの連続する値の間では、他に可能な x の値がなく、ジャンプがないため、分布関数は変化しません。 最終的に、最後の可能な値 x M の点で、確率値 p M だけジャンプがあり、分布関数は 1 に等しい限界値に達します。 さらに、グラフはこのレベルで x 軸に平行になります。 確率が 1 より大きくなることはあり得ないため、これより高くなることはありません。

3.2.4. 連続確率変数の分布を表す方法

連続確率変数は、その分布関数によっても与えられ、原則として分析形式で提示されます。 さらに、分布関数 F(x) の一次導関数である確率密度関数 f(x) によって完全に説明できます。

確率密度関数は非負であり、無限限界での積分は 1 に等しい。

例として、通常の法則に従って分布する連続確率変数を取り上げます。

その確率密度関数は、次の形式の式によって分析的に与えられます。

ここで、m X と σ X は分布パラメーターです。 m X は分布中心の位置を特徴付け、σ X - この「中心」に対する分散。

「学校での確率論」 - 複雑な出来事。 いくつかのテスト。 基本イベントの空間の任意のサブセット。 確率。 特定の条件セットの実装。 独立したイベント。 確率乗法定理。 製品ルール。 イベントが発生する可能性が最も高い回数。 相容れない事象の確率の加法定理。

「ランダムイベントの確率」 - 初歩的なイベント。 左右対称のコインを 2 回投げます。 サイコロを 1 つ投げます。 ランダムな実験の基本的なイベント。 確率の合計。 縁起の良いエレメンタル イベント。 シューター。 サッカーの試合。 初歩的な出来事の表。 右のコインを投げることによって。 同等の基本イベント。

「確率の加算と乗算」 - 確率の乗算と加算の定理。 少なくとも 1 つのイベントが発生する確率。 特別なケース。 独立したイベント。 乗算定理。 全確率式。 確率の加算の定理。 ターゲットに命中する確率。 確率乗法定理。 すべてのイベント。 条件付き確率。

「試験の確率論」 - 転がしたポイントの合計が 6 になる確率。 有利な出来事 A. 積則（掛け算の法則）。 袋には黒玉2個と白玉3個が入っています。 順列、配置、組み合わせの違い。 イベントの確率。 教材。 真ん中に書いてある数字。

「事象の発生確率」 - 自然数。 イベントの確率の決定。 実験。 確率の推定の可能性。 組み合わせ。 確率。 場所。 反対のイベントの確率。 イベントの確率。 ケース数。 組み合わせ論の要素。 要素の数。 確率論の要素。 イベントの確率の統計的定義。

「確率変数」 - ベルヌーイの公式。 狭い長方形。 分布関数を構築するために、その値のいくつかを計算します。 分布関数は非減少関数です。 SWの分配法則は任意の比率です。 仕事。 確率変数 (CV)。 SW値の異なる間隔。 この関数は、いわば SW の分布密度を表しています。

トピックの合計 23 プレゼンテーション

離散確率変数を指定する方法は一般的ではありません。たとえば、連続確率変数には適用できません。 実際、確率変数 X の可能な値が区間 (a;b) を完全に満たすようにします。 X のすべての可能な値のリストを作成することは可能ですか? いいえ。 任意のタイプの確率変数を指定する一般的な方法が必要です。 この目的のために、確率変数の確率分布関数が導入されます。

分布関数 分布関数は関数 F(x) と呼ばれ、テストの結果として確率変数 X が x より小さい値を取る確率を決定します。 F(x) = P(X

X 1. 3. 3. 確率変数が値を取る確率が結論付けられます" title="(!LANG: 分布関数のプロパティ 1. 1. 分布関数の値は次のセグメントに属します: 0 F(x) 1. 2. 2. F (x) - 非減少関数、つまり F (x 2) F (x 1)、x 2 > x 1 の場合。 3. 3. 確率変数が値をとります" class="link_thumb"> 4 !}分布関数のプロパティ 分布関数の値は次の区間に属します: 0 F(x) F(x) - 非減少関数、つまり F(x 2) F(x 1)、x 2 > x の場合確率変数が区間 (a; b) に含まれる値を取る確率は、この区間での分布関数の増分に等しくなります: P (a x 1. 3. 3. 確率変数が区間 (a; b) に含まれる値を取る確率は、この区間での分布関数の増分に等しくなります: P (a "\u003e x 1. 3 . 3. 確率変数が値を取る確率, 結論" title = "(!LANG: 分布関数のプロパティ 1. 1. 分布関数の値は、間隔に属します: 0 F( x ) 1. 2. 2. F (x) - 非減少関数、つまり F (x 2) F (x 1)、x 2 > x 1 の場合。 3. 3. 確率変数が価値"> title="分布関数のプロパティ 1. 1. 分布関数の値は次の区間に属します: 0 F(x) 1. 2. 2. F(x) は非減少関数、つまり F(x 2) F(x 1) (x 2 > x 1 の場合) 3. 3. 確率変数が値を取る確率は、"> !}

例 1. 確率変数 X は、x -1 で 0 の分布関数によって与えられます。 F(x) = x/4+1/4 at 検定の結果、X が次の値を取る確率を求めます。間隔 (0; 2): P(0

4. 4. 連続確率変数 X が 1 つの明確な値を取る確率は 0 です。したがって、任意に小さい場合でも、確率変数が区間に入る確率を考慮することは理にかなっています。 たとえば、部品の寸法が許容範囲を超えない確率に関心がありますが、設計サイズと一致する確率の問題は提起しません。

しかし、確率 P(X=x 1) が 0 に等しいということは、イベント X=x 1 が不可能であることを意味すると考えるのは誤りです (確率の古典的な定義に限定されない場合)。 テストの結果、確率変数は必ず可能な値の 1 つを取ります。 特に、この値は x 1 に等しい場合があります。

5. 5. 確率変数の可能な値が区間 (a;b) に属する場合、1) F(x) = 0 for x a; 2) F(x) = 1 for x b. ] 連続確率変数の可能な値が x 軸全体にある場合、次の極限関係が有効です。 Lim F(x) = 0; リム F(x) = 1. x- x+

連続確率変数の確率分布の密度 分布関数を使用して連続確率変数を設定する方法は、唯一のものではありません。 連続確率変数は、分布密度または確率密度と呼ばれる別の関数 (微分関数と呼ばれることもあります) を使用して指定することもできます。

連続確率変数 X の確率分布密度は、関数 f (x) - 分布関数 F (x) の 1 次導関数: f (x) \u003d F "(x) です。したがって、分布関数は逆導関数です。分布密度について。

π/2。 分布密度 f(x) を求めます。 x π/2 に対して 0。 ). x π/2 の場合は 0。" class="link_thumb"> 18 !}例。 x 0 における連続確率変数 X 0 の分布関数 F(x) = 0 π/2 における sinx が与えられます。 分布密度 f(x) を求めます。 x π/2 の場合は 0。 π/2。 分布密度 f(x) を求めます。 x π/2 の場合は 0."> π/2. 分布密度 f(x) を求めます。x π/2 の場合は 0."> π/2. 分布密度 f(x) を求めます。 x π/2 に対して 0。 ). x π/2 の場合は 0。"> (x) = cosx при 0 π/2." title="例。 x 0 における連続確率変数 X 0 の分布関数 F(x) = 0 π/2 における sinx が与えられます。 分布密度 f(x) を求めます。 x π/2 の場合は 0。"> !}

分布密度の性質 分布密度は非負の関数です: f(x) 0. 分布密度のプロットは分布曲線と呼ばれます. - から までの範囲の分布密度の不適切な積分は 1 に等しくなります. f(x) dx = 1. -

分布密度の確率的意味 関数 f(x) は、各点 x の確率分布密度を決定します。 十分に小さい x の場合。 F(x + x) - F(x) f(x)x. なぜなら 差 F (x + x) - F (x) は、X が間隔 (x; x + x) に属する値を取る確率を決定します (上記を参照)。この確率は、したがって、積にほぼ等しくなります。間隔 x の長さによる m. x の確率密度。

Ⅱ． ランダム値、その分布関数

2.1. 確率変数、設定方法

ランダム テストの結果、1つまたは別の数値をとることができる量が呼び出され、どれがどれであるかは事前にわかりません。

ある量について、実質的に同じ条件下で何度も測定を繰り返すと、毎回多少異なる結果が得られることがわかります。 これは、2 種類の原因の影響です。1) 結果の主な重要性を決定する主な原因。 2) 二次的で、それらの発散を引き起こします。

これらの原因の共同作用の下では、必然性と偶然性の概念は密接に関連していることが判明するが、必然性が偶発性よりも優勢である.

したがって、確率変数の可能な値は、いくつかの数値セットに属します。

これらのセットでは、量が任意の値を取ることができるのはランダムですが、事前にどの値になるかはわかりません。

ランダム変数は、ランダム イベントに関連付けられます。

ランダムイベントなら 品質特性 テストの場合、確率変数はその 量的特徴 .

確率変数は大文字のラテン文字で示され、その値は大文字で示されます。
.

確率変数が
意味を持っていきます 支持する：

等

確率変数は分布法則によって与えられます。

確率変数の分布法則 確率変数の可能な値とその確率の間に確立された対応です。

分布法則は、表、グラフ、分析の 3 つの方法で指定できます。 確率変数の種類によって設定方法が異なります。

確率変数には主に 2 つのタイプがあります。 離散および連続分布確率変数。

2.2. 離散確率変数と連続確率変数

与えられた確率変数が取ることができる値が、離散 (有限または無限) の数列を形成する場合
次に、確率変数自体が呼び出されます 離散。

この確率変数が取り得る値が、数値軸の有限または無限のギャップ (a, c) を満たす場合 おー、次に、確率変数が呼び出されます 連続。

離散型確率変数の各値 ある確率に相当する ; 連続型の確率変数の範囲からの各区間 (a, c) も、特定の確率に対応します
確率変数によって受け入れられた値がこの間隔内にあるという事実。

2.3. 確率変数の分布法則

何らかの方法で、確率変数の可能な値とその確率の間の関係を確立する関係は、 分配法 ランダム変数。

離散確率変数の分布法則は、通常、次の式で与えられます。 近い分布:

その中で
、ここで、合計は、指定された確率変数の可能な値のセット全体 (有限または無限) に拡張されます。

連続確率変数の分布法則は、以下を使用して便利に指定されます。 確率密度関数
.

確率変数が取る値が区間 (a, c) に入る確率は、等式によって決定されます。

関数のグラフが呼び出されます 分布曲線 . 幾何学的には、確率変数が間隔 (a、c) に入る確率は、分布曲線によって囲まれた、対応する曲線台形の面積に等しくなります。 おーそして直接 x=a、x=b。

タスク1。確率変数の値の確率が与えられます。値 10 の確率は 0.3 です。 値 2 - 確率 0.4; 値 8 - 確率 0.1; 値 4 – 確率 0.2。 確率変数 の分布系列を構築します。

解決。確率変数の値を昇順に並べると、分布系列が得られます。

飛行機に乗ろう コーラスポイント (2; 0.4)、(4; 0.2)、(8; 0.1) および (10; 0.3)。 連続する点を直線セグメントで結ぶと、 ポリゴン （また ポリゴン ) 確率変数の分布

タスク 2。それぞれ 5,000 ルーブル相当のアイテムが 2 つと、30,000 ルーブル相当のアイテムが 1 つ再生されます。 50 枚中 1 枚のチケットを購入した人の賞金分配の法則を作成します。

解決。 目的の確率変数は勝利であり、0、5,000、30,000 ルーブルの 3 つの値を取ることができます。 最初の結果は 47 件、2 番目の結果は 2 件、3 番目の結果は 1 件有利です。 それらの確率を見つけてみましょう：

; ; .

確率変数の分布法則は、次の形式をとります。

テストとして、

タスク 3。確率変数は、密度 の分布法則に従い、

必須: 1) 係数 a を見つけます。 2) 密度分布をプロットする
; 3) 間隔 (1; 2) に入る確率を見つけます。

解決。 1) この確率変数のすべての値が区間に含まれているため、

、 どこ

、 また

、つまり
.

2) 区間内の関数のグラフは放物線であり、この区間外では横座標自体がグラフとして機能します。

3) 確率変数が区間 (1; 2) に入る確率は、等式から求めることができます。

2.4. 二項分布

特定の数を生産する n独立した実験であり、それらのそれぞれで同じ確率で何らかのイベントが発生する可能性があります R. イベントの発生回数である確率変数を考えてみましょう あの n実験。 その分布法則は次の形をしています

値
確率

どこ
、ベルヌーイの公式で計算されます。

このような表を特徴とする分布法則を 二項式 .

仕事。コインを5回投げます。 紋章の喪失数 - 確率変数の分布法則を構成します。

解決。 可能性のある確率変数の値は次のとおりです: 0、1、2、3、4、5。ベルヌーイの公式を使用した確率変数:

分配法則は次の形をしています。

値
確率

確認しよう：

III. ランダム値の期待値と分散

3.1. 離散確率変数の数学的期待値

確率変数の最も包括的な特性は、その確率分布の法則です。 ただし、必ずしも分配法則のすべてを知っている必要はありません。 確率変数の「平均値」の意味を持つ数値や、確率変数の平均サイズを示す数値など、分布法則の最も重要な特徴を反映する 1 つ以上の数値でうまくいく場合があります。確率変数の平均値からの偏差。 そのような番号は呼ばれます 数値特性 ランダム変数。 数値特性を利用すれば、分布法則を使わなくても多くの問題を解くことができます。

確率変数の最も重要な数値特性の 1 つは、数学的な期待値です。

分布法則が次の形式を持つ離散確率変数が既知の場合

値
確率

それから 数学的期待値 離散量の (または平均値) は数と呼ばれます

したがって、離散確率変数の数学的期待値は、この変数の可能な値とその確率の積の合計に等しくなります。

例 1. その分布の法則を知って、確率変数の数学的期待値を見つけます

解決。

数学的期待値の特性。

定数係数は、期待値記号から取り出すことができます。

定数値の数学的期待値 からは次の値と等しい:

2 つの確率変数の合計の数学的期待値は、それらの数学的期待値の合計に等しくなります。

独立確率変数の積の数学的期待値は、これらの変数の数学的期待値の積に等しくなります。

3.2. 確率変数の標準偏差と分散。

例 2確率変数の数学的期待値を求め、 それらの分布の法則を知る

P

興味深い結果が得られました。量の分布の法則と は異なりますが、それらの数学的期待値は同じです。

図面から b数量の値が数学的期待値の周りにより集中していることがわかります
量の値よりも、その数学的期待値に対して散らばっています (散らばっています)
（写真 a).

数学的期待値に対する確率変数の値の分散度の主な数値特性
は分散であり、次のように表されます。
.

意味。 偏差 確率変数とその数学的期待値の差、つまり
.

偏差とその二乗
も確率変数です。

意味。 離散分散 確率変数は、その偏差の 2 乗の数学的な期待値と呼ばれます。

分散特性。

分散定数 から 0:

.

.

分散を計算するには、式の方が便利です

例 3離散確率変数は次の法則に従って分布します。

解決。 まず、 を見つけます。

その後
.

私たちが持っている式によって

確率変数の標準偏差 はその分散の平方根と呼ばれます。

.

IV. セルフコントロールのための実践的な課題

組み合わせ論

1、3、5、7、9 の 5 桁の数は、同じ数字が重複しない場合、何通りできますか?

抽選に 7 チームが参加した場合、3 つの賞品を配布するオプションはいくつありますか?

グループに 33 人がいる場合、会議のために 2 人の学生を選ぶ方法は何通りありますか?

方程式を解く

a)
. b)
.

5 で割り切れる 4 桁の数は、0、1、2、5、7 の各数字に同じ数字が含まれてはならない場合、これらの数字から何個作ることができますか?

15人のグループから、職長と旅団の4人のメンバーを選択する必要があります。 これはいくつの方法で行うことができますか?

モールス符号文字は記号 (ドットとダッシュ) で構成されています。 各文字が 5 文字以内である必要がある場合、何文字を表すことができますか?

7本の異なる色のリボンで4色のリボンを作る方法は何通りありますか?

9 人の候補者から 4 つの異なる役職に 4 人を選ぶ方法は何通りありますか?

6枚のカードから3枚を選ぶ方法は何通りありますか?

卒業前に、30 人の学生のグループが写真を交換しました。 配られた写真の数。

お祝いのテーブルで 10 人のゲストが 10 か所に座るには、何通りの方法がありますか?

1ラウンドのチャンピオンシップで、20のサッカーチームが何試合を行う必要がありますか?

各チームに 6 人がいる場合、12 人をチームに分ける方法は何通りありますか?

確率論

壷には、7 つの赤と 6 つの青のボールが含まれています。 2つのボールが同時に壷から取り出されます。 両方のボールが赤である確率 (イベント A) は?

1つの棚に9冊の本がランダムに並べられています。 ある本が 4 冊並べて置かれる確率 (事象 C) を求めよ.

10 枚中 2 枚が当選 ランダムに取った 5 枚のチケットのうち 1 枚が当選する確率を求めよ.

カードのデッキ (52 枚のカード) から 3 枚のカードがランダムに引き出されます。 スリー、セブン、エースである確率を求めよ。

子供は分割アルファベット A、K、R、W、Y の 5 文字で遊んでいます。 文字をランダムに一列に並べた場合、彼が「屋根」という単語を受け取る確率はどのくらいですか。

箱の中には白玉が6個、赤玉が4個入っています。 2つのボールがランダムに取られます。 それらが同じ色である確率は?

最初の骨壷には黒ボールが 6 個と白ボールが 4 個入っており、2 番目の骨壺には黒ボールが 5 個と白ボールが 7 個入っています。 各壷から 1 つのボールが引き出されます。 両方のボールが白である確率は?

確率変数、確率変数の数学的期待値と分散

1発で命中する確率が0.4の場合、6発で標的に命中する回数の分布法則を書きなさい。

生徒が必要な本を図書館で見つける確率は 0.3 です。 市内に 4 つの図書館がある場合、彼が訪問する図書館の数の分配法を作成します。

ハンターは最初のヒットの前にゲームを撃ちますが、4発しか撃ちません。 一発で的中する確率が 0.7 のときの、的を外した回数の分散を求めよ。

分布の法則が次の表で与えられる場合、確率変数 X の数学的な期待値を求めます。

工場には4つの自動ラインがあります。 作業シフト中に最初の行が調整を必要としない確率は 0.9、2 番目は 0.8、3 番目は 0.75、4 番目は 0.7 です。 勤務シフト中に調整を必要としないライン数の数学的期待値を見つけます。

確率変数 X の分散を求め、その分布の法則を知っています。

ダンコ P.E. 演習と課題における高等数学。 2 つの部分で。 パート II / 体育 Danko, A.G. ポポフ、T.Ya。 コジェフニコフ。 - M.: Higher School, 1986. - 415 p. Vygodsky M.Ya。 高等数学のハンドブック。 – M.: Nauka、1975. – 872 p. 追加： グリグレツキー V.G. 経済専門の学生のための数学。 パート 2 / V.G. Griguletsky、I.V。 Lukyanova、I.A。 ペチュニナ。 - クラスノダール、2002. - 348 p. マリキン V.I. 経済学における数学。 – M.: Infra-M, 1999. – 356 p. グサク A.A. 高等数学。 2巻で、V.2。 - 大学生向けの教科書。 – M.: テトラシステムズ、1988 年 – 448 ページ。 グリグレツキー V.G. 高等数学 / V.G. グリグレツキー、Z.V. ヤシチェンコ。 – クラスノダール、1998.-186 p. Gmurman V.E. 確率論と数理統計の問題を解くためのガイド。 - M.: Higher School, 2000. - 400 p.

フェイスブック

ツイッター

連絡先

同級生

Google+