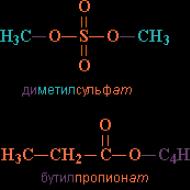
8 sayısının 4 tabanına göre logaritması. Logaritma nedir? Bir sayı logaritma olarak nasıl yazılır?

Gizliliğinizin korunması bizim için önemlidir. Bu nedenle bilgilerinizi nasıl kullandığımızı ve sakladığımızı açıklayan bir Gizlilik Politikası geliştirdik. Lütfen gizlilik uygulamalarımızı inceleyin ve herhangi bir sorunuz varsa bize bildirin.

Kişisel bilgilerin toplanması ve kullanılması

Kişisel bilgiler, belirli bir kişiyi tanımlamak veya onunla iletişim kurmak için kullanılabilecek verileri ifade eder.

Bizimle iletişime geçtiğinizde istediğiniz zaman kişisel bilgilerinizi vermeniz istenebilir.

Aşağıda toplayabileceğimiz kişisel bilgi türlerine ve bu bilgileri nasıl kullanabileceğimize dair bazı örnekler verilmiştir.

Hangi kişisel bilgileri topluyoruz:

• Siteye bir başvuru gönderdiğinizde adınız, telefon numaranız, e-posta adresiniz vb. dahil olmak üzere çeşitli bilgiler toplayabiliriz.

Kişisel bilgilerinizi nasıl kullanıyoruz:

• Topladığımız kişisel bilgiler, benzersiz teklifler, promosyonlar, diğer etkinlikler ve gelecek etkinlikler konusunda sizinle iletişim kurmamıza olanak tanır.
• Zaman zaman kişisel bilgilerinizi önemli bildirimler ve iletişimler göndermek için kullanabiliriz.
• Kişisel bilgileri, sunduğumuz hizmetleri geliştirmek ve size hizmetlerimizle ilgili tavsiyeler sunmak amacıyla denetimler, veri analizi ve çeşitli araştırmalar yapmak gibi şirket içi amaçlarla da kullanabiliriz.
• Bir ödül çekilişine, yarışmaya veya benzer bir promosyona katılırsanız, sağladığınız bilgileri bu tür programları yönetmek için kullanabiliriz.

Bilgilerin üçüncü şahıslara açıklanması

Sizden aldığımız bilgileri üçüncü şahıslara açıklamıyoruz.

İstisnalar:

• Gerekirse - yasaya, adli prosedüre uygun olarak, yasal işlemlerde ve/veya kamunun talepleri veya Rusya Federasyonu topraklarındaki hükümet yetkililerinin talepleri temelinde - kişisel bilgilerinizi ifşa etmek. Ayrıca, bu tür bir açıklamanın güvenlik, kanun yaptırımı veya diğer kamu önemi amaçları açısından gerekli veya uygun olduğunu tespit etmemiz halinde, hakkınızdaki bilgileri de açıklayabiliriz.
• Yeniden yapılanma, birleşme veya satış durumunda topladığımız kişisel bilgileri ilgili halef üçüncü tarafa aktarabiliriz.

Kişisel bilgilerin korunması

Kişisel bilgilerinizi kayıp, hırsızlık ve kötüye kullanımın yanı sıra yetkisiz erişime, ifşa edilmeye, değiştirilmeye ve imhaya karşı korumak için idari, teknik ve fiziksel önlemler alıyoruz.

Şirket düzeyinde gizliliğinize saygı duymak

Kişisel bilgilerinizin güvende olduğundan emin olmak için gizlilik ve güvenlik standartlarını çalışanlarımıza aktarıyor ve gizlilik uygulamalarını sıkı bir şekilde uyguluyoruz.

Bildiğiniz gibi ifadeleri kuvvetlerle çarparken üsleri daima toplanır (a b *a c = a b+c). Bu matematik kanunu Arşimet tarafından türetildi ve daha sonra 8. yüzyılda matematikçi Virasen tamsayı üslerinden oluşan bir tablo oluşturdu. Logaritmanın daha fazla keşfedilmesine hizmet edenler onlardı. Bu işlevin kullanımına ilişkin örnekler, zahmetli çarpma işlemlerini basit toplama yoluyla basitleştirmeniz gereken hemen hemen her yerde bulunabilir. Bu makaleyi okumaya 10 dakikanızı ayırırsanız size logaritmanın ne olduğunu ve onlarla nasıl çalışılacağını açıklayacağız. Basit ve erişilebilir bir dille.

Matematikte tanım

Logaritma aşağıdaki formun bir ifadesidir: log a b=c, yani negatif olmayan herhangi bir sayının (yani herhangi bir pozitif) “b”nin “a” tabanına göre logaritması, “c” kuvveti olarak kabul edilir. ” sonuçta "b" değerini elde etmek için "a" tabanının yükseltilmesi gerekir. Logaritmayı örneklerle inceleyelim, diyelim ki log 2 8 ifadesi var. Cevap nasıl bulunur? Çok basit, öyle bir güç bulmanız gerekiyor ki 2'den gerekli güce 8 ulaşacaksınız. Kafanızda bazı hesaplamalar yaptıktan sonra 3 sayısını elde ediyoruz! Ve bu doğru çünkü 2 üssü 3 cevabı 8 olarak veriyor.

Logaritma türleri

Pek çok öğrenci ve öğrenci için bu konu karmaşık ve anlaşılmaz görünüyor, ancak aslında logaritmalar o kadar da korkutucu değil, asıl önemli olan genel anlamlarını anlamak ve özelliklerini ve bazı kurallarını hatırlamaktır. Üç ayrı logaritmik ifade türü vardır:

1. Doğal logaritma ln a, burada taban Euler sayısıdır (e = 2,7).
2. Tabanı 10 olan ondalık a.
3. Herhangi bir b sayısının a>1 tabanına göre logaritması.

Bunların her biri, logaritmik teoremler kullanılarak basitleştirme, indirgeme ve ardından tek bir logaritmaya indirgeme dahil olmak üzere standart bir şekilde çözülür. Logaritmaların doğru değerlerini elde etmek için, bunları çözerken özelliklerini ve eylem sırasını hatırlamanız gerekir.

Kurallar ve bazı kısıtlamalar

Matematikte aksiyom olarak kabul edilen, yani tartışmaya konu olmayan ve gerçek olan birçok kural-kısıtlama vardır. Örneğin sayıları sıfıra bölmek mümkün olmadığı gibi negatif sayıların çift kökünü çıkarmak da imkansızdır. Logaritmaların da kendi kuralları vardır; bunları takip ederek uzun ve kapsamlı logaritmik ifadelerle bile çalışmayı kolayca öğrenebilirsiniz:

• "a" tabanı her zaman sıfırdan büyük olmalı ve 1'e eşit olmamalıdır, aksi takdirde ifade anlamını kaybeder, çünkü "1" ve "0" herhangi bir dereceye kadar her zaman değerlerine eşittir;
• a > 0 ise a b >0 ise "c"nin de sıfırdan büyük olması gerektiği ortaya çıkar.

Logaritmalar nasıl çözülür?

Örneğin 10 x = 100 denkleminin cevabını bulma görevi veriliyor. Bu çok kolay, on sayısını artırarak 100'e ulaşacağımız bir kuvvet seçmeniz gerekiyor. Bu elbette 10 2 = 100.

Şimdi bu ifadeyi logaritmik formda gösterelim. Log 10 100 = 2 elde ederiz. Logaritmaları çözerken, belirli bir sayıyı elde etmek için logaritmanın tabanına girmenin gerekli olduğu gücü bulmak için tüm eylemler pratik olarak birleşir.

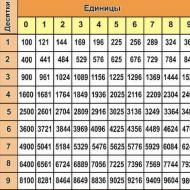
Bilinmeyen bir derecenin değerini doğru bir şekilde belirlemek için derece tablosuyla nasıl çalışılacağını öğrenmeniz gerekir. Şuna benziyor:

Gördüğünüz gibi, eğer teknik bir aklınız ve çarpım tablosu bilginiz varsa, bazı üsler sezgisel olarak tahmin edilebilir. Ancak daha büyük değerler için güç tablosuna ihtiyacınız olacaktır. Karmaşık matematik konuları hakkında hiçbir şey bilmeyen kişiler tarafından bile kullanılabilir. Sol sütun sayıları içerir (a tabanı), sayıların üst satırı a sayısının yükseltildiği c kuvvetinin değeridir. Kesişme noktasında hücreler cevap olan sayı değerlerini içerir (a c =b). Mesela 10 rakamının olduğu ilk hücreyi alıp karesini alalım, iki hücremizin kesişiminde gösterilen 100 değerini elde ederiz. Her şey o kadar basit ve kolaydır ki en gerçek hümanist bile anlayacaktır!

Denklemler ve eşitsizlikler

Belirli koşullar altında üssün logaritma olduğu ortaya çıktı. Bu nedenle herhangi bir matematiksel sayısal ifade logaritmik eşitlik olarak yazılabilir. Örneğin 3 4 =81, 81'in 3 tabanlı logaritması dörde eşit (log 3 81 = 4) olarak yazılabilir. Negatif kuvvetler için kurallar aynıdır: 2 -5 = 1/32 logaritma olarak yazarsak log 2 (1/32) = -5 elde ederiz. Matematiğin en büyüleyici bölümlerinden biri “logaritmalar” konusudur. Özelliklerini inceledikten hemen sonra aşağıdaki denklem örneklerine ve çözümlerine bakacağız. Şimdi eşitsizliklerin neye benzediğine ve onları denklemlerden nasıl ayıracağımıza bakalım.

Aşağıdaki ifade verilmiştir: log 2 (x-1) > 3 - bu logaritmik bir eşitsizliktir, çünkü bilinmeyen “x” değeri logaritmik işaretin altındadır. Ayrıca ifadede iki nicelik karşılaştırılır: İstenilen sayının iki tabanına göre logaritması üç sayısından büyüktür.

Logaritmik denklemler ve eşitsizlikler arasındaki en önemli fark, logaritmalı denklemlerin (örneğin, logaritma 2 x = √9) cevapta bir veya daha fazla spesifik sayısal değeri ima etmesi, bir eşitsizliği çözerken ise her iki kabul edilebilir değer aralığının da belirtilmesidir. Bu fonksiyon kırılarak değerler ve noktalar belirlenir. Sonuç olarak cevap, bir denklemin cevabında olduğu gibi basit bir bireysel sayılar dizisi değil, sürekli bir dizi veya sayı dizisidir.

Logaritmalarla ilgili temel teoremler

Logaritmanın değerlerini bulma gibi ilkel görevleri çözerken özellikleri bilinmeyebilir. Ancak konu logaritmik denklemler veya eşitsizlikler olduğunda öncelikle logaritmanın tüm temel özelliklerini net bir şekilde anlamak ve pratikte uygulamak gerekir. Daha sonra denklem örneklerine bakacağız; önce her özelliğe daha ayrıntılı olarak bakalım.

1. Ana kimlik şuna benzer: a logaB =B. Bu yalnızca a'nın 0'dan büyük olması, bire eşit olmaması ve B'nin sıfırdan büyük olması durumunda geçerlidir.
2. Çarpımın logaritması şu formülle temsil edilebilir: log d (s 1 * s 2) = log d s 1 + log d s 2. Bu durumda zorunlu koşul şudur: d, s 1 ve s 2 > 0; a≠1. Bu logaritmik formülün ispatını örneklerle ve çözümle yapabilirsiniz. Log a s 1 = f 1 ve log a s 2 = f 2 olsun, sonra a f1 = s 1, a f2 = s 2 olsun. s 1 * s 2 = a f1 *a f2 = a f1+f2 sonucunu elde ederiz (özellikleri derece ) ve ardından tanım gereği: log a (s 1 * s 2) = f 1 + f 2 = log a s1 + log a s 2, bunun kanıtlanması gerekiyordu.
3. Bölümün logaritması şuna benzer: log a (s 1/ s 2) = log a s 1 - log a s 2.
4. Formül biçimindeki teorem şu biçimi alır: log a q b n = n/q log a b.

Bu formüle “logaritma derecesinin özelliği” denir. Sıradan derecelerin özelliklerine benzer ve bu şaşırtıcı değildir çünkü tüm matematik doğal önermelere dayanmaktadır. Kanıta bakalım.

Log a b = t olsun, a t =b olur. Her iki parçayı da m kuvvetine çıkarırsak: a tn = b n ;

ancak a tn = (a q) nt/q = b n olduğundan, log a q b n = (n*t)/t olduğundan, log a q b n = n/q log a b olur. Teorem kanıtlandı.

Sorun ve eşitsizlik örnekleri

Logaritmalarla ilgili en yaygın problem türleri denklem ve eşitsizlik örnekleridir. Neredeyse tüm problem kitaplarında bulunurlar ve aynı zamanda matematik sınavlarının da zorunlu bir parçasıdırlar. Bir üniversiteye girmek veya matematikte giriş sınavlarını geçmek için bu tür görevleri nasıl doğru bir şekilde çözeceğinizi bilmeniz gerekir.

Ne yazık ki, logaritmanın bilinmeyen değerini çözmek ve belirlemek için tek bir plan veya şema yoktur, ancak her matematiksel eşitsizliğe veya logaritmik denkleme belirli kurallar uygulanabilir. Öncelikle ifadenin basitleştirilip sadeleştirilemeyeceğini veya genel bir forma indirgenip indirgenemeyeceğini öğrenmelisiniz. Uzun logaritmik ifadeleri, özelliklerini doğru kullanırsanız basitleştirebilirsiniz. Onları hızlıca tanıyalım.

Logaritmik denklemleri çözerken, ne tür bir logaritmaya sahip olduğumuzu belirlememiz gerekir: örnek bir ifade, doğal bir logaritma veya ondalık bir logaritma içerebilir.

İşte ln100, ln1026 örnekleri. Çözümleri, 10 tabanının sırasıyla 100 ve 1026'ya eşit olacağı gücü belirlemeleri gerektiği gerçeğine dayanıyor. Doğal logaritmaları çözmek için logaritmik kimlikleri veya bunların özelliklerini uygulamanız gerekir. Çeşitli türlerdeki logaritmik problemleri çözme örneklerine bakalım.

Logaritma Formülleri Nasıl Kullanılır: Örnekler ve Çözümlerle

Şimdi logaritmalarla ilgili temel teoremlerin kullanımına ilişkin örneklere bakalım.

1. Bir çarpımın logaritmasının özelliği, b sayısının büyük bir değerini daha basit faktörlere ayırmanın gerekli olduğu görevlerde kullanılabilir. Örneğin, log 2 4 + log 2 128 = log 2 (4*128) = log 2 512. Cevap 9'dur.
2. log 4 8 = log 2 2 2 3 = 3/2 log 2 2 = 1,5 - gördüğünüz gibi logaritmanın kuvvetinin dördüncü özelliğini kullanarak, görünüşte karmaşık ve çözülemez bir ifadeyi çözmeyi başardık. Tabanı çarpanlara ayırmanız ve ardından üs değerlerini logaritmanın işaretinden çıkarmanız yeterlidir.

Birleşik Devlet Sınavından Ödevler

Logaritmalara genellikle giriş sınavlarında, özellikle de Birleşik Devlet Sınavında (tüm okul mezunları için devlet sınavı) birçok logaritmik problemle karşılaşılır. Genellikle bu görevler yalnızca A bölümünde (sınavın en kolay test kısmı) değil, aynı zamanda C bölümünde de (en karmaşık ve hacimli görevler) mevcuttur. Sınav, “Doğal logaritmalar” konusunda doğru ve mükemmel bilgi gerektirir.

Sorunlara örnekler ve çözümler Birleşik Devlet Sınavının resmi versiyonlarından alınmıştır. Bu tür görevlerin nasıl çözüldüğünü görelim.

Log 2 (2x-1) = 4 verildiğinde. Çözüm:
ifadeyi biraz basitleştirerek yeniden yazalım log 2 (2x-1) = 2 2, logaritmanın tanımından 2x-1 = 2 4, dolayısıyla 2x = 17 elde ederiz; x = 8,5.

• Çözümün hantal ve kafa karıştırıcı olmaması için tüm logaritmaların aynı tabana indirilmesi en iyisidir.
• Logaritmanın işaretinin altındaki tüm ifadeler pozitif olarak gösterilir, dolayısıyla logaritmanın işaretinin altında olan bir ifadenin tabanı çarpan olarak üssü çıkarıldığında logaritmanın altında kalan ifadenin pozitif olması gerekir.

\(a^(b)=c\) \(\Leftrightarrow\) \(\log_(a)(c)=b\)

Daha basit bir şekilde açıklayalım. Örneğin, \(\log_(2)(8)\), \(8\) elde etmek için \(2\)'nin yükseltilmesi gereken kuvvete eşittir. Bundan \(\log_(2)(8)=3\) olduğu açıktır.

Argüman ve logaritmanın tabanı

Herhangi bir logaritma aşağıdaki “anatomiye” sahiptir:

Bir logaritmanın argümanı genellikle kendi düzeyinde yazılır ve tabanı, logaritma işaretine daha yakın bir alt simgeyle yazılır. Ve bu girdi şu şekilde okunur: "Yirmi beşin beş tabanına göre logaritması."

Logaritma nasıl hesaplanır?

Logaritmayı hesaplamak için şu soruyu yanıtlamanız gerekir: Tartışmayı elde etmek için taban hangi güce yükseltilmelidir?

Örneğin, logaritmayı hesaplayın: a) \(\log_(4)(16)\) b) \(\log_(3)\)\(\frac(1)(3)\) c) \(\log_(\ sqrt (5))(1)\) d) \(\log_(\sqrt(7))(\sqrt(7))\) e) \(\log_(3)(\sqrt(3))\)

a) \(16\) elde etmek için \(4\) hangi kuvvete yükseltilmelidir? Açıkçası ikincisi. Bu yüzden:

\(\log_(4)(16)=2\)

\(\log_(3)\)\(\frac(1)(3)\) \(=-1\)

c) \(1\) elde etmek için \(\sqrt(5)\) hangi kuvvete yükseltilmelidir? Hangi güç herhangi bir numarayı bir numara yapar? Elbette sıfır!

\(\log_(\sqrt(5))(1)=0\)

d) \(\sqrt(7)\) elde etmek için \(\sqrt(7)\) hangi kuvvete yükseltilmelidir? Öncelikle herhangi bir sayının birinci kuvveti kendisine eşittir.

\(\log_(\sqrt(7))(\sqrt(7))=1\)

e) \(\sqrt(3)\) elde etmek için \(3\) hangi kuvvete yükseltilmelidir? Bunun kesirli bir kuvvet olduğunu biliyoruz, yani karekök \(\frac(1)(2)\)'nin kuvvetidir.

\(\log_(3)(\sqrt(3))=\)\(\frac(1)(2)\)

Örnek : Logaritmayı hesaplayın \(\log_(4\sqrt(2))(8)\)

Çözüm :

Cevap : \(\log_(4\sqrt(2))(8)=1,2\)

Logaritma neden icat edildi?

Bunu anlamak için denklemi çözelim: \(3^(x)=9\). Denklemin çalışması için \(x\) ile eşleşmeniz yeterli. Elbette \(x=2\).

Şimdi denklemi çözün: \(3^(x)=8\).x neye eşittir? Önemli olan bu.

En akıllıları şunu söyleyecektir: "X ikiden biraz küçüktür." Bu sayı tam olarak nasıl yazılır? Bu soruyu cevaplamak için logaritma icat edildi. Onun sayesinde buradaki cevap \(x=\log_(3)(8)\) şeklinde yazılabilir.

Şunu vurgulamak istiyorum: \(\log_(3)(8)\), mesela herhangi bir logaritma sadece bir sayıdır. Evet, sıradışı görünüyor ama kısa. Çünkü bunu ondalık sayı olarak yazmak isteseydik şu şekilde görünürdü: \(1.892789260714.....\)

Örnek : \(4^(5x-4)=10\) denklemini çözün

Çözüm :

Cevap : \(\frac(\log_(4)(10)+4)(5)\)

Ondalık ve doğal logaritmalar

Logaritmanın tanımında belirtildiği gibi tabanı \((a>0, a\neq1)\) dışında herhangi bir pozitif sayı olabilir. Ve tüm olası tabanlar arasında, o kadar sık ​​görülen iki taban var ki, bunlarla logaritmalar için özel bir kısa notasyon icat edildi:

Doğal logaritma: tabanı Euler sayısı \(e\) (yaklaşık olarak \(2,7182818…\)'a eşit) olan ve logaritma \(\ln(a)\) şeklinde yazılan bir logaritma.

Yani, \(\ln(a)\) \(\log_(e)(a)\) ile aynıdır

Ondalık Logaritma: Tabanı 10 olan logaritma \(\lg(a)\) olarak yazılır.

Yani, \(\lg(a)\) \(\log_(10)(a)\) ile aynıdır, burada \(a\) bir sayıdır.

Temel logaritmik kimlik

Logaritmaların birçok özelliği vardır. Bunlardan birine “Temel Logaritmik Kimlik” denir ve şuna benzer:

Bu özellik doğrudan tanımdan kaynaklanmaktadır. Bu formülün tam olarak nasıl ortaya çıktığını görelim.

Logaritmanın tanımına ilişkin kısa bir notasyonu hatırlayalım:

eğer \(a^(b)=c\), o zaman \(\log_(a)(c)=b\)

Yani \(b\), \(\log_(a)(c)\) ile aynıdır. Daha sonra \(a^(b)=c\) formülünde \(b\) yerine \(\log_(a)(c)\) yazabiliriz. Ana logaritmik kimlik olan \(a^(\log_(a)(c))=c\) ortaya çıktı.

Logaritmanın diğer özelliklerini bulabilirsiniz. Onların yardımıyla, doğrudan hesaplanması zor olan ifadelerin değerlerini logaritmalarla basitleştirebilir ve hesaplayabilirsiniz.

Örnek : \(36^(\log_(6)(5))\) ifadesinin değerini bulun

Çözüm :

Cevap : \(25\)

Bir sayı logaritma olarak nasıl yazılır?

Yukarıda belirtildiği gibi, herhangi bir logaritma yalnızca bir sayıdır. Bunun tersi de doğrudur: Herhangi bir sayı logaritma olarak yazılabilir. Örneğin, \(\log_(2)(4)\)'un ikiye eşit olduğunu biliyoruz. Daha sonra iki yerine \(\log_(2)(4)\) yazabilirsiniz.

Ancak \(\log_(3)(9)\) aynı zamanda \(2\)'ye eşittir, bu da \(2=\log_(3)(9)\) yazabileceğimiz anlamına gelir. Aynı şekilde \(\log_(5)(25)\) ve \(\log_(9)(81)\), vb. ile. Yani ortaya çıkıyor

\(2=\log_(2)(4)=\log_(3)(9)=\log_(4)(16)=\log_(5)(25)=\log_(6)(36)=\ log_(7)(49)...\)

Dolayısıyla, eğer ihtiyacımız varsa, ikiyi herhangi bir yerde herhangi bir tabana sahip logaritma olarak yazabiliriz (bir denklemde, bir ifadede veya bir eşitsizlikte) - sadece tabanın karesini argüman olarak yazabiliriz.

Üçlü için de durum aynıdır; \(\log_(2)(8)\), \(\log_(3)(27)\) veya \(\log_(4)() olarak yazılabilir. 64) \)... Burada küpteki tabanı argüman olarak yazıyoruz:

\(3=\log_(2)(8)=\log_(3)(27)=\log_(4)(64)=\log_(5)(125)=\log_(6)(216)=\ log_(7)(343)...\)

Ve dört ile:

\(4=\log_(2)(16)=\log_(3)(81)=\log_(4)(256)=\log_(5)(625)=\log_(6)(1296)=\ log_(7)(2401)...\)

Ve eksi bir ile:

\(-1=\) \(\log_(2)\)\(\frac(1)(2)\) \(=\) \(\log_(3)\)\(\frac(1)( 3)\) \(=\) \(\log_(4)\)\(\frac(1)(4)\) \(=\) \(\log_(5)\)\(\frac(1) )(5)\) \(=\) \(\log_(6)\)\(\frac(1)(6)\) \(=\) \(\log_(7)\)\(\frac (1)(7)\) \(...\)

Ve üçte biriyle:

\(\frac(1)(3)\) \(=\log_(2)(\sqrt(2))=\log_(3)(\sqrt(3))=\log_(4)(\sqrt( 4))=\log_(5)(\sqrt(5))=\log_(6)(\sqrt(6))=\log_(7)(\sqrt(7))...\)

Herhangi bir \(a\) sayısı, \(b\) tabanına sahip bir logaritma olarak temsil edilebilir: \(a=\log_(b)(b^(a))\)

Örnek : İfadenin anlamını bulun \(\frac(\log_(2)(14))(1+\log_(2)(7))\)

Çözüm :

Cevap : \(1\)

Logaritma Belirli bir sayının üssüne, başka bir sayının yükseltilmesi gereken üssü denir. temel Bu sayıyı elde etmek için logaritma. Örneğin 100'ün 10 tabanındaki logaritması 2'dir. Yani 100'ü elde etmek için 10'un karesi alınmalıdır (10 2 = 100). Eğer N– belirli bir sayı, B– taban ve ben– logaritma, o halde b ben = n. Sayı N taban antilogaritma olarak da adlandırılır B sayılar ben. Örneğin 2'nin 10 tabanına göre antilogaritması 100'e eşittir. Bu, ilişkiler günlüğü şeklinde yazılabilir. bn = ben ve antilog b l = N.

Logaritmanın temel özellikleri:

Biri dışında herhangi bir pozitif sayı, logaritmaların temeli olabilir, ancak ne yazık ki şu ortaya çıkıyor: B Ve N rasyonel sayılardır, o zaman nadir durumlarda böyle bir rasyonel sayı vardır ben, Ne b ben = n. Ancak irrasyonel bir sayı tanımlamak mümkündür. benörneğin, öyle ki 10 ben= 2; bu irrasyonel bir sayı ben rasyonel sayılarla gerekli herhangi bir doğrulukla tahmin edilebilir. Verilen örnekte ortaya çıkıyor ben yaklaşık olarak 0,3010'a eşittir ve 2'nin 10 tabanlı logaritmasının bu yaklaşımı, dört basamaklı ondalık logaritma tablolarında bulunabilir. 10 tabanlı logaritmalar (veya 10 tabanlı logaritmalar) hesaplamalarda o kadar yaygın olarak kullanılır ki bunlara denir. sıradan logaritmalar ve log2 = 0,3010 veya log2 = 0,3010 olarak yazılır, logaritmanın tabanının açık göstergesi atlanır. Tabana göre logaritmalar e, yaklaşık olarak 2,71828'e eşit olan aşkın bir sayıya denir doğal logaritmalar. Esas olarak matematiksel analiz ve bunun çeşitli bilimlerdeki uygulamalarına ilişkin çalışmalarda bulunurlar. Doğal logaritmalar da tabanı açıkça belirtmeden, ancak özel ln gösterimi kullanılarak yazılır: örneğin, ln2 = 0,6931, çünkü e 0,6931 = 2.

Sıradan logaritma tablolarının kullanılması.

Bir sayının normal logaritması, belirli bir sayıyı elde etmek için 10'a yükseltilmesi gereken bir üstür. 10 0 = 1, 10 1 = 10 ve 10 2 = 100 olduğundan, hemen log1 = 0, log10 = 1, log100 = 2 vb. değerlerini elde ederiz. 10'un tam sayı kuvvetlerini arttırmak için. Aynı şekilde, 10 –1 = 0,1, 10 –2 = 0,01 ve dolayısıyla log0,1 = –1, log0,01 = –2, vb. tüm negatif tam sayı kuvvetleri için 10. Geriye kalan sayıların olağan logaritmaları, 10'un en yakın tam sayı kuvvetlerinin logaritmaları arasına alınır; log2 0 ile 1 arasında, log20 1 ile 2 arasında ve log0.2 -1 ile 0 arasında olmalıdır. Dolayısıyla logaritma, 0 ile 1 arasında yer alan bir tam sayı ve bir ondalık sayı olmak üzere iki bölümden oluşur. tamsayı kısmı denir karakteristik logaritma ve sayının kendisi tarafından belirlenir, kesirli kısım denir mantis ve tablolardan bulunabilir. Ayrıca log20 = log(2ґ10) = log2 + log10 = (log2) + 1. 2'nin logaritması 0,3010'dur, yani log20 = 0,3010 + 1 = 1,3010. Benzer şekilde log0.2 = log(2о10) = log2 – log10 = (log2) – 1 = 0.3010 – 1. Çıkarma işleminden sonra log0.2 = – 0.6990 elde ederiz. Ancak log0.2'yi 0,3010 – 1 veya 9,3010 – 10 olarak temsil etmek daha uygundur; Genel bir kural da formüle edilebilir: belirli bir sayıdan 10'un kuvvetleriyle çarpılarak elde edilen tüm sayılar, verilen sayının mantisine eşit aynı mantislere sahiptir. Çoğu tablo, 1'den 10'a kadar olan aralıktaki sayıların mantislerini gösterir, çünkü diğer tüm sayıların mantisleri tabloda verilenlerden elde edilebilir.

Çoğu tablo, dört veya beş ondalık basamaklı logaritmalar verir, ancak yedi basamaklı tablolar ve daha fazla ondalık basamaklı tablolar da vardır. Bu tür tabloların nasıl kullanılacağını öğrenmenin en kolay yolu örneklerdir. Log3.59'u bulmak için öncelikle 3.59 sayısının 10 0 ile 10 1 arasında olduğunu, yani karakteristiğinin 0 olduğunu not ediyoruz. Tabloda 35 sayısını (solda) buluyoruz ve satır boyunca üst kısmında 9 rakamı bulunan sütun; bu sütun ile 35. satırın kesişimi 5551'dir, yani log3.59 = 0.5551. Dört anlamlı basamaklı bir sayının mantisini bulmak için enterpolasyonu kullanmalısınız. Bazı tablolarda enterpolasyon, tabloların her sayfasının sağ tarafındaki son dokuz sütunda verilen oranlar sayesinde kolaylaştırılmıştır. Şimdi log736.4'ü bulalım; 736.4 sayısı 10 2 ile 10 3 arasındadır, dolayısıyla logaritmasının özelliği 2'dir. Tabloda solunda 73 ve 6 numaralı sütunların bulunduğu bir satır buluyoruz. Bu satır ile bu sütunun kesişiminde 8669 sayısı. Doğrusal parçalar arasında 4. sütunu buluyoruz. 73. satır ile 4. sütunun kesişiminde 2 sayısı var. 8669'a 2 ekleyerek mantis elde ederiz - 8671'e eşittir. Böylece log736.4 = 2.8671.

Doğal logaritmalar.

Doğal logaritmanın tabloları ve özellikleri, sıradan logaritmanın tabloları ve özelliklerine benzer. Her ikisi arasındaki temel fark, doğal logaritmanın tamsayı kısmının ondalık noktanın konumunu belirlemede önemli olmaması ve dolayısıyla mantis ile karakteristik arasındaki farkın özel bir rol oynamamasıdır. 5.432 sayısının doğal logaritması; 54,32 ve 543,2 sırasıyla 1,6923'e eşittir; 3,9949 ve 6,2975. Bu logaritmalar arasındaki ilişki, aralarındaki farklara bakıldığında daha da netleşecektir: log543.2 – log54.32 = 6,2975 – 3,9949 = 2,3026; son sayı 10 sayısının doğal logaritmasından başka bir şey değildir (şu şekilde yazılır: ln10); log543.2 – log5.432 = 4.6052; son sayı 2ln10'dur. Ancak 543,2 = 10'54,32 = 10 2'5,432. Böylece, belirli bir sayının doğal logaritmasına göre A sayıların çarpımlarına eşit sayıların doğal logaritmasını bulabilirsiniz A herhangi bir derece için N 10 sayısı ln ise A ln10 ile çarpılarak ekle N yani In( Aґ10N) = günlük A + N ln10 = ln A + 2,3026N. Örneğin, ln0,005432 = ln(5,432ґ10 –3) = ln5,432 – 3ln10 = 1,6923 – (3ґ2,3026) = – 5,2155. Bu nedenle, doğal logaritma tabloları, sıradan logaritma tabloları gibi, genellikle yalnızca 1'den 10'a kadar sayıların logaritmasını içerir. Doğal logaritma sisteminde antilogaritmalardan söz edilebilir, ancak daha çok üstel bir fonksiyondan veya bir üs hakkında konuşurlar. Eğer X= günlük sen, O sen = eski, Ve senüssü denir X(tipografik kolaylık sağlamak için sıklıkla yazarlar sen= deneyim X). Üs, sayının antilogaritmasının rolünü oynar X.

Ondalık ve doğal logaritma tablolarını kullanarak, 10'dan başka herhangi bir tabanda logaritma tabloları oluşturabilirsiniz. e. Günlük ise ba bir = X, O bx = A ve bu nedenle günlük cbx= günlük CA veya X kayıt cb= günlük CA, veya X= günlük CA/kayıt cb= günlük ba bir. Bu nedenle, temel logaritma tablosundan bu ters çevirme formülünü kullanarak C başka herhangi bir tabanda logaritma tabloları oluşturabilirsiniz B. Çarpan 1/günlük cb isminde geçiş modülü tabandan Cüsse B. Örneğin ters çevirme formülünün kullanılmasını veya bir logaritma sisteminden diğerine geçişi, sıradan logaritma tablosundan doğal logaritmaların bulunmasını veya ters geçiş yapılmasını hiçbir şey engellemez. Örneğin, log105.432 = log e 5.432/günlük e 10 = 1,6923/2,3026 = 1,6923ґ0,4343 = 0,7350. Sıradan bir logaritma elde etmek için belirli bir sayının doğal logaritmasının çarpılması gereken 0,4343 sayısı, sıradan logaritma sistemine geçiş modülüdür.

Özel tablolar.

Logaritmalar başlangıçta özellik loglarını kullanarak icat edildi. ab= günlük A+ günlük B ve kayıt A/B= günlük A-kayıt B, ürünleri toplamlara, bölümleri farklara dönüştürün. Başka bir deyişle, eğer günlük A ve kayıt B biliniyorsa, toplama ve çıkarma işlemlerini kullanarak çarpımın ve bölümün logaritmasını kolayca bulabiliriz. Ancak astronomide sıklıkla log değerleri verilir A ve kayıt B günlüğü bulmam gerekiyor( A + B) veya günlük( A – B). Elbette ilk olarak logaritma tablolarından bulunabilir. A Ve B, daha sonra belirtilen toplama veya çıkarma işlemini yapın ve yine tablolara bakarak gerekli logaritmaları bulun, ancak böyle bir prosedür tablolara üç kez bakmayı gerektirir. Z. Leonelli 1802'de sözde tabloları yayınladı. Gauss logaritmaları– toplamların ve farkların eklenmesi için logaritmalar – bu da tablolara tek bir erişimin sınırlandırılmasını mümkün kıldı.

1624'te I. Kepler orantılı logaritma tabloları önerdi; sayıların logaritmaları A/X, Nerede A– bazı pozitif sabit değerler. Bu tablolar öncelikle gökbilimciler ve gezginler tarafından kullanılır.

Orantılı logaritmalar A= 1 denir eşologaritmalar ve çarpımlar ve bölümlerle uğraşmak gerektiğinde hesaplamalarda kullanılır. Bir sayının kologaritması N karşılıklı sayının logaritmasına eşit; onlar. kolonya N= günlük1/ N= – günlük N. Log2 = 0,3010 ise, colog2 = – 0,3010 = 0,6990 – 1. Koloaritma kullanmanın avantajı, aşağıdaki gibi ifadelerin logaritmasının değerini hesaplarken olmasıdır. pq/R pozitif ondalık sayıların üçlü toplamı günlüğü P+ günlük Q+kolog R karışık toplam ve fark logunu bulmaktan daha kolaydır P+ günlük Q-kayıt R.

Hikaye.

Herhangi bir logaritma sisteminin altında yatan prensip çok uzun zamandır bilinmektedir ve kökeni eski Babil matematiğine (M.Ö. 2000 civarı) kadar uzanabilmektedir. O günlerde bileşik faiz hesaplamak için tam sayıların pozitif tam sayı kuvvetlerinin tablo değerleri arasında enterpolasyon kullanılıyordu. Çok daha sonra Arşimet (MÖ 287-212), o zamanlar bilinen Evreni tamamen doldurmak için gereken kum tanesi sayısına ilişkin bir üst sınır bulmak için 108'in katlarını kullandı. Arşimed, logaritmanın etkinliğinin altında yatan üslü sayılar özelliğine dikkat çekti: kuvvetlerin çarpımı üslerin toplamına karşılık gelir. Orta Çağ'ın sonu ve modern çağın başlangıcında matematikçiler giderek geometrik ve aritmetik ilerlemeler arasındaki ilişkiye yönelmeye başladılar. M. Stiefel makalesinde Tamsayı Aritmetiği(1544) 2 sayısının pozitif ve negatif kuvvetlerini gösteren bir tablo verdi:

Stiefel, ilk satırdaki (üs satırı) iki sayının toplamının, alt satırdaki (üs satırı) karşılık gelen iki sayının çarpımına karşılık gelen iki üssüne eşit olduğunu fark etti. Bu tabloyla bağlantılı olarak Stiefel, üslü işlemler için dört modern kurala veya logaritma işlemleri için dört kurala eşdeğer dört kural formüle etti: üst satırdaki toplam, alt satırdaki çarpıma karşılık gelir; üst satırdaki çıkarma işlemi alt satırdaki bölme işlemine karşılık gelir; üst satırdaki çarpma, alt satırdaki üstel sayıya karşılık gelir; Üst satırdaki bölünme, alt satırdaki köklenmeye karşılık gelir.

Görünen o ki, Stiefel'in kurallarına benzer kurallar, J. Naper'in çalışmalarında ilk logaritma sistemini resmi olarak tanıtmasına yol açmıştır. Şaşırtıcı logaritma tablosunun açıklaması Ancak Napier'in düşünceleri, çarpımları toplamlara dönüştürme sorunuyla meşguldü; o zamandan beri, çalışmasının yayınlanmasından on yıldan fazla bir süre önce Napier, Danimarka'dan Tycho Brahe Gözlemevi'nde asistanlarının bunu yapan bir yönteme sahip olduğuna dair bir haber aldı. Ürünleri toplamlara dönüştürmek mümkündür. Napier'in aldığı mesajda tartışılan yöntem, aşağıdaki gibi trigonometrik formüllerin kullanımına dayanıyordu:

bu nedenle Naper'in tabloları esas olarak trigonometrik fonksiyonların logaritmasından oluşuyordu. Her ne kadar Napier tarafından önerilen tanımda taban kavramı açıkça yer almasa da, onun sisteminde logaritma sisteminin tabanına eşdeğer rol, yaklaşık olarak 1/'e eşit olan (1 – 10 –7)`10 7 sayısı tarafından oynanıyordu. e.

Naper'den bağımsız olarak ve neredeyse onunla eşzamanlı olarak, tip olarak oldukça benzer bir logaritma sistemi J. Bürgi tarafından Prag'da icat edildi ve yayınlandı, 1620'de yayınlandı. Aritmetik ve geometrik ilerleme tabloları. Bunlar (1 + 10 –4) ґ10 4 tabanına göre antilogaritma tablolarıydı; sayının oldukça iyi bir tahmini e.

Naper sisteminde 10 7 sayısının logaritması sıfır alınmış, sayılar azaldıkça logaritmalar artmaktaydı. G. Briggs (1561–1631) Napier'i ziyaret ettiğinde her ikisi de 10 sayısını taban olarak kullanmanın ve birin logaritmasını sıfır olarak kabul etmenin daha uygun olacağı konusunda hemfikirdi. Daha sonra sayılar arttıkça logaritmaları da artacaktır. Böylece Briggs'in tablosunu çalışmasında yayınladığı modern ondalık logaritma sistemini elde ettik. Logaritmik aritmetik(1620). Tabana göre logaritmalar e Her ne kadar tam olarak Naper tarafından tanıtılanlar olmasa da, genellikle Naper's olarak anılırlar. "Karakteristik" ve "mantis" terimleri Briggs tarafından önerildi.

İlk logaritmalar, tarihsel nedenlerden dolayı, 1/ sayılarına yaklaşık değerler kullandı. e Ve e. Bir süre sonra doğal logaritma fikri hiperbol altındaki alanların incelenmesiyle ilişkilendirilmeye başlandı. xy= 1 (Şekil 1). 17. yüzyılda bu eğrinin sınırladığı alanın, eksenin olduğu gösterildi X ve koordinatlar X= 1 ve X = A(Şekil 1'de bu alan daha kalın ve seyrek noktalarla kaplıdır) aşağıdaki durumlarda aritmetik ilerleme artar: A katlanarak artar. Üslü ve logaritmalı işlemlere ilişkin kurallarda ortaya çıkan tam da bu bağımlılıktır. Bu, Naperian logaritmalarının "hiperbolik logaritmalar" olarak adlandırılmasına yol açtı.

Logaritmik fonksiyon.

Logaritmanın yalnızca bir hesaplama aracı olarak kabul edildiği bir dönem vardı, ancak 18. yüzyılda esas olarak Euler'in çalışmaları sayesinde logaritmik fonksiyon kavramı oluşturuldu. Böyle bir fonksiyonun grafiği sen= günlük X Koordinatları aritmetik bir ilerlemeyle artarken apsisleri geometrik bir ilerlemeyle artan Şekil 2'de gösterilmektedir. 2, A. Ters veya üstel bir fonksiyonun grafiği y = ex Geometrik ilerlemede koordinatları artan ve aritmetik ilerlemede apsisleri artan, sırasıyla Şekil 2'de gösterilmektedir. 2, B. (Eğriler sen= günlük X Ve sen = 10Xşekil olarak eğrilere benzer sen= günlük X Ve sen = eski.) Logaritmik fonksiyonun alternatif tanımları da önerilmiştir;

kpı; ve benzer şekilde -1 sayısının doğal logaritmaları (2) biçimindeki karmaşık sayılardır. k + 1)pi, Nerede k- Bir tam sayı. Benzer ifadeler genel logaritmalar veya diğer logaritma sistemleri için de geçerlidir. Ek olarak, logaritmanın tanımı, karmaşık sayıların karmaşık logaritmasını içerecek şekilde Euler kimlikleri kullanılarak genelleştirilebilir.

Logaritmik bir fonksiyonun alternatif bir tanımı fonksiyonel analizle sağlanır. Eğer F(X) – bir gerçek sayının sürekli fonksiyonu X aşağıdaki üç özelliğe sahiptir: F (1) = 0, F (B) = 1, F (UV) = F (sen) + F (v), O F(X) sayının logaritması olarak tanımlanır X dayalı B. Bu tanımın, bu makalenin başında verilen tanıma göre birçok avantajı vardır.

Uygulamalar.

Logaritmalar başlangıçta yalnızca hesaplamaları basitleştirmek için kullanıldı ve bu uygulama hala en önemlilerinden biridir. Çarpımların, bölümlerin, kuvvetlerin ve köklerin hesaplanması, yalnızca yayınlanmış logaritma tablolarının geniş çapta bulunmasıyla değil, aynı zamanda sözde kullanımıyla da kolaylaştırılmıştır. sürgülü hesap cetveli - çalışma prensibi logaritmanın özelliklerine dayanan bir hesaplama aracıdır. Cetvel logaritmik ölçeklerle donatılmıştır; 1 numaradan herhangi bir numaraya olan mesafe X loga eşit olacak şekilde seçilmiş X; Bir ölçeği diğerine göre kaydırarak, logaritmaların toplamlarını veya farklarını çizmek mümkündür; bu, ilgili sayıların çarpımlarını veya bölümlerini doğrudan ölçekten okumayı mümkün kılar. Sayıları logaritmik biçimde temsil etmenin avantajlarından da yararlanabilirsiniz. grafikleri çizmek için logaritmik kağıt (her iki koordinat ekseninde üzerine logaritmik ölçekler basılmış kağıt). Bir fonksiyon formun güç yasasını karşılıyorsa y = kxn o zaman logaritmik grafiği düz bir çizgiye benzer çünkü kayıt sen= günlük k + N kayıt X– loga göre doğrusal denklem sen ve kayıt X. Aksine, eğer bazı fonksiyonel bağımlılığın logaritmik grafiği düz bir çizgi gibi görünüyorsa, bu bağımlılık bir kuvvettir. Yarı logaritmik kağıt (y ekseninin logaritmik bir ölçeğe sahip olduğu ve x ekseninin tek biçimli bir ölçeğe sahip olduğu), üstel fonksiyonları tanımlamanız gerektiğinde kullanışlıdır. Formun denklemleri y = kb rx Nüfus, radyoaktif madde miktarı veya banka bakiyesi gibi bir miktar, nüfus, radyoaktif madde veya mevcut para miktarıyla orantılı bir oranda azaldığında veya arttığında meydana gelir. Böyle bir bağımlılık yarı logaritmik kağıda çizilirse grafik düz bir çizgi gibi görünecektir.

Logaritmik fonksiyon, çok çeşitli doğal formlarla bağlantılı olarak ortaya çıkar. Ayçiçeği salkımlarındaki çiçekler logaritmik spiraller halinde düzenlenir, yumuşakça kabukları bükülür Nautilus, dağ koyunu boynuzları ve papağan gagaları. Bu doğal şekillerin tümü, logaritmik spiral olarak bilinen bir eğrinin örnekleri olarak hizmet edebilir, çünkü kutupsal bir koordinat sisteminde denklemi şöyledir: r = ae bq, veya ln R= günlük A + bq. Böyle bir eğri, kutuptan uzaklığı geometrik ilerlemeyle artan ve yarıçap vektörüyle açıklanan açı aritmetik ilerlemeyle artan hareketli bir noktayla tanımlanır. Böyle bir eğrinin ve dolayısıyla logaritmik fonksiyonun her yerde bulunması, bunun eksantrik bir kamın konturu ve ışığa doğru uçan bazı böceklerin yörüngesi gibi uzak ve tamamen farklı alanlarda meydana gelmesi gerçeğiyle iyi bir şekilde gösterilmiştir.