x की जड़ का ग्राफ़. x का x मूल बराबर है. उदाहरण। जड़ की जड़

पावर फ़ंक्शन के मूल गुण दिए गए हैं, जिनमें जड़ों के सूत्र और गुण शामिल हैं। पावर फ़ंक्शन का व्युत्पन्न, अभिन्न, पावर श्रृंखला विस्तार और जटिल संख्या प्रतिनिधित्व प्रस्तुत किया गया है।

सामग्री

एक घात फलन, y = x p, घातांक p के साथ निम्नलिखित गुण हैं:
(1.1) सेट पर परिभाषित और निरंतर
पर ,
पर ;
(1.2) के कई अर्थ हैं
पर ,
पर ;
(1.3) सख्ती से बढ़ता है,
के रूप में सख्ती से घटता है;
(1.4) पर ;
पर ;
(1.5) ;
(1.5*) ;
(1.6) ;
(1.7) ;
(1.7*) ;
(1.8) ;
(1.9) .

गुणों का प्रमाण "पावर फ़ंक्शन (निरंतरता और गुणों का प्रमाण)" पृष्ठ पर दिया गया है

जड़ें - परिभाषा, सूत्र, गुण

किसी संख्या x की घात n का मूल वह संख्या है जिसे घात n तक बढ़ाने पर x प्राप्त होता है:
.
यहाँ n= 2, 3, 4, ... - एक से बड़ी प्राकृतिक संख्या।

आप यह भी कह सकते हैं कि घात n वाली संख्या x का मूल समीकरण का मूल (अर्थात् समाधान) है
.
ध्यान दें कि फ़ंक्शन, फ़ंक्शन का व्युत्क्रम है।

x का वर्गमूल दूसरा मूल है: .
x का घनमूल तीसरा मूल है: .

यहां तक ​​कि डिग्री भी

सम घातों के लिए n = 2 मी, मूल को x ≥ के लिए परिभाषित किया गया है 0 . अक्सर उपयोग किया जाने वाला सूत्र सकारात्मक और नकारात्मक x दोनों के लिए मान्य है:
.
वर्गमूल के लिए:
.

जिस क्रम में संचालन किया जाता है वह यहां महत्वपूर्ण है - यानी, पहले वर्ग निष्पादित किया जाता है, जिसके परिणामस्वरूप एक गैर-नकारात्मक संख्या होती है, और फिर मूल इससे लिया जाता है (वर्गमूल एक गैर-नकारात्मक संख्या से लिया जा सकता है) ). यदि हमने क्रम बदल दिया:, तो ऋणात्मक x के लिए मूल अपरिभाषित होगा, और इसके साथ संपूर्ण अभिव्यक्ति अपरिभाषित होगी।

अजीब डिग्री

विषम शक्तियों के लिए, मूल को सभी x के लिए परिभाषित किया गया है:
;
.

जड़ों के गुण एवं सूत्र

x का मूल एक घात फलन है:
.
जब x ≥ 0 निम्नलिखित सूत्र लागू होते हैं:
;
;
, ;
.

ये सूत्र चरों के ऋणात्मक मानों के लिए भी लागू किये जा सकते हैं। आपको बस यह सुनिश्चित करने की आवश्यकता है कि सम शक्तियों की मौलिक अभिव्यक्ति नकारात्मक न हो।

निजी मूल्य

0 का मूल 0: है।
मूल 1, 1 के बराबर है:।
0 का वर्गमूल 0: है।
1 का वर्गमूल 1: है।

उदाहरण। जड़ की जड़

आइए जड़ों के वर्गमूल का एक उदाहरण देखें:
.
आइए उपरोक्त सूत्रों का उपयोग करके आंतरिक वर्गमूल को रूपांतरित करें:
.
आइए अब मूल रूट को रूपांतरित करें:
.
इसलिए,
.

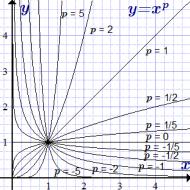
घातांक p के विभिन्न मानों के लिए y = x p।

यहां तर्क x के गैर-नकारात्मक मानों के लिए फ़ंक्शन के ग्राफ़ दिए गए हैं। x के नकारात्मक मानों के लिए परिभाषित पावर फ़ंक्शन के ग्राफ़ "पावर फ़ंक्शन, इसके गुण और ग्राफ़" पृष्ठ पर दिए गए हैं।

उलटा काम करना

घातांक p के साथ एक घात फलन का व्युत्क्रम घातांक 1/p के साथ एक घात फलन है।

तो अगर।

एक शक्ति फलन का व्युत्पन्न

nवें क्रम का व्युत्पन्न:
;

सूत्र व्युत्पन्न करना > > >

पावर फ़ंक्शन का अभिन्न अंग

पी ≠ - 1 ;
.

शक्ति शृंखला विस्तार

पर - 1 < x < 1 निम्नलिखित अपघटन होता है:

सम्मिश्र संख्याओं का उपयोग करते हुए व्यंजक

जटिल चर z के फ़ंक्शन पर विचार करें:
एफ (जेड) = जेड टी.
आइए हम जटिल चर z को मापांक r और तर्क φ (r = |z|) के संदर्भ में व्यक्त करें:
z = r e i φ .
हम सम्मिश्र संख्या t को वास्तविक और काल्पनिक भागों के रूप में निरूपित करते हैं:
टी = पी + आई क्यू .
हमारे पास है:

इसके बाद, हम इस बात को ध्यान में रखते हैं कि तर्क φ विशिष्ट रूप से परिभाषित नहीं है:
,

आइए उस मामले पर विचार करें जब q = 0 , अर्थात, घातांक एक वास्तविक संख्या है, t = p. तब
.

यदि p एक पूर्णांक है, तो kp एक पूर्णांक है। फिर, त्रिकोणमितीय कार्यों की आवधिकता के कारण:
.
अर्थात्, किसी दिए गए z के लिए पूर्णांक घातांक वाले घातांकीय फ़ंक्शन का केवल एक ही मान होता है और इसलिए यह स्पष्ट है।

यदि p अपरिमेय है, तो किसी भी k के लिए गुणनफल kp पूर्णांक उत्पन्न नहीं करता है। चूँकि k मानों की एक अनंत श्रृंखला से होकर गुजरता है के = 0, 1, 2, 3, ..., तो फलन z p में अपरिमित रूप से अनेक मान हैं। जब भी तर्क z बढ़ाया जाता है 2π(एक मोड़ पर), हम फ़ंक्शन की एक नई शाखा में जाते हैं।

यदि p परिमेय है, तो इसे इस प्रकार दर्शाया जा सकता है:
, कहाँ एम, एन- पूर्णांक जिनमें उभयनिष्ठ भाजक नहीं होते। तब
.
पहले n मान, k = k के साथ 0 = 0, 1, 2, ...एन-1, kp के n भिन्न मान दें:
.
हालाँकि, बाद के मान ऐसे मान देते हैं जो पिछले वाले से एक पूर्णांक से भिन्न होते हैं। उदाहरण के लिए, जब k = k 0+एनहमारे पास है:
.
त्रिकोणमितीय फ़ंक्शन जिनके तर्क गुणकों से भिन्न होते हैं 2π, समान मूल्य हैं। इसलिए, k में और वृद्धि के साथ, हमें z p का वही मान प्राप्त होता है जो k = k के लिए होता है 0 = 0, 1, 2, ...एन-1.

इस प्रकार, एक तर्कसंगत घातांक वाला एक घातांकीय फलन बहुमूल्यांकित होता है और इसमें n मान (शाखाएँ) होते हैं। जब भी तर्क z बढ़ाया जाता है 2π(एक मोड़ पर), हम फ़ंक्शन की एक नई शाखा में जाते हैं। ऐसी क्रांतियों के बाद हम पहली शाखा पर लौटते हैं जहाँ से उलटी गिनती शुरू हुई थी।

विशेष रूप से, डिग्री n के मूल में n मान होते हैं। उदाहरण के तौर पर, एक वास्तविक धनात्मक संख्या z = x के nवें मूल पर विचार करें। इस मामले में φ 0 = 0 , z = r = |z| = एक्स, .
.
तो, एक वर्गमूल के लिए, n = 2 ,
.
सम k के लिए, (- 1 ) के = 1. विषम k के लिए, (- 1 ) के = - 1.
अर्थात वर्गमूल के दो अर्थ होते हैं: + और -।

सन्दर्भ:
में। ब्रोंस्टीन, के.ए. सेमेन्डयेव, इंजीनियरों और कॉलेज के छात्रों के लिए गणित की पुस्तिका, "लैन", 2009।

यह सभी देखें:

एक प्राथमिक फलन के रूप में वर्गमूल।

वर्गमूलएक प्राथमिक कार्य है और पावर फ़ंक्शन का एक विशेष मामला है। अंकगणितीय वर्गमूल सुचारू है, और शून्य पर यह निरंतर है लेकिन भिन्न नहीं है।

एक फ़ंक्शन के रूप में, एक जटिल चर रूट एक दो-मूल्य वाला फ़ंक्शन होता है जिसकी पत्तियाँ शून्य पर एकत्रित होती हैं।

वर्गमूल फ़ंक्शन का रेखांकन.

1. डेटा तालिका भरना:

एक्स
पर

2. हम निर्देशांक तल पर प्राप्त बिंदुओं को आलेखित करते हैं।

3. इन बिंदुओं को जोड़ें और वर्गमूल फ़ंक्शन का ग्राफ़ प्राप्त करें:

वर्गमूल फ़ंक्शन के ग्राफ़ को बदलना।

आइए हम यह निर्धारित करें कि फ़ंक्शन ग्राफ़ बनाने के लिए कौन से फ़ंक्शन परिवर्तन किए जाने की आवश्यकता है। आइए परिवर्तनों के प्रकारों को परिभाषित करें।

	रूपांतरण प्रकार	परिवर्तन
		किसी फ़ंक्शन को किसी अक्ष के अनुदिश स्थानांतरित करना ओए 4 इकाइयों के लिए ऊपर।
	आंतरिक	किसी फ़ंक्शन को किसी अक्ष के अनुदिश स्थानांतरित करना बैल 1 यूनिट के लिए दांई ओर।
	आंतरिक	ग्राफ़ अक्ष के पास पहुंचता है ओए 3 बार और अक्ष के अनुदिश संपीड़ित करें ओह.
		ग्राफ़ अक्ष से दूर चला जाता है बैल ओए.
	आंतरिक	ग्राफ़ अक्ष से दूर चला जाता है ओए 2 बार और अक्ष के अनुदिश खींचा गया ओह.

अक्सर, फ़ंक्शन परिवर्तन संयुक्त होते हैं।

उदाहरण के लिए, आपको फ़ंक्शन को प्लॉट करने की आवश्यकता है . यह एक वर्गमूल ग्राफ़ है जिसे अक्ष से एक इकाई नीचे ले जाने की आवश्यकता है ओएऔर अक्ष के अनुदिश दाईं ओर एक इकाई ओहऔर साथ ही इसे अक्ष के अनुदिश 3 बार खींचे ओए.

ऐसा होता है कि किसी फ़ंक्शन का ग्राफ़ बनाने से तुरंत पहले, प्रारंभिक पहचान परिवर्तन या फ़ंक्शन के सरलीकरण की आवश्यकता होती है।

क्या आपने x बराबर का x मूल खोजा? . विवरण और स्पष्टीकरण के साथ एक विस्तृत समाधान आपको सबसे जटिल समस्या से निपटने में मदद करेगा, और x, y का मूल है, कोई अपवाद नहीं है। हम आपको होमवर्क, टेस्ट, ओलंपियाड के साथ-साथ विश्वविद्यालय में प्रवेश के लिए तैयारी करने में मदद करेंगे। और इससे कोई फर्क नहीं पड़ता कि कौन सा उदाहरण है, इससे कोई फर्क नहीं पड़ता कि आप कौन सी गणित क्वेरी दर्ज करते हैं, हमारे पास पहले से ही एक समाधान है। उदाहरण के लिए, "x, x बराबर का मूल है।"

विभिन्न गणितीय समस्याओं, कैलकुलेटर, समीकरणों और फ़ंक्शंस का उपयोग हमारे जीवन में व्यापक है। इनका उपयोग कई गणनाओं, संरचनाओं के निर्माण और यहां तक ​​कि खेलों में भी किया जाता है। मनुष्य प्राचीन काल से ही गणित का प्रयोग करता आया है और तब से इसका प्रयोग बढ़ता ही गया है। हालाँकि, अब विज्ञान स्थिर नहीं है और हम इसकी गतिविधि के फल का आनंद ले सकते हैं, जैसे कि एक ऑनलाइन कैलकुलेटर जो x का मूल बराबर, y का x मूल, x का मूल, x का मूल बराबर जैसी समस्याओं को हल कर सकता है। x, x का मूल x के बराबर है, x का मूल x के बराबर है, फ़ंक्शन y, शून्य x का मूल है, फ़ंक्शन y, x का मूल घटा है, x, y का मूल है, x, x का मूल है, x के बराबर है। इस पृष्ठ पर आपको एक कैलकुलेटर मिलेगा जो आपको किसी भी प्रश्न को हल करने में मदद करेगा, जिसमें x के बराबर का x मूल भी शामिल है। (उदाहरण के लिए, x का मूल)।

आप गणित में किसी भी समस्या को कहां हल कर सकते हैं, साथ ही x का मूल x बराबर ऑनलाइन कहां है?

आप हमारी वेबसाइट पर x बराबर के x मूल की समस्या का समाधान कर सकते हैं। मुफ़्त ऑनलाइन सॉल्वर आपको किसी भी जटिलता की ऑनलाइन समस्या को कुछ ही सेकंड में हल करने की अनुमति देगा। आपको बस सॉल्वर में अपना डेटा दर्ज करना है। आप हमारी वेबसाइट पर वीडियो निर्देश भी देख सकते हैं और अपना कार्य सही ढंग से दर्ज करना सीख सकते हैं। और यदि आपके पास अभी भी प्रश्न हैं, तो आप उन्हें कैलकुलेटर पृष्ठ के नीचे बाईं ओर चैट में पूछ सकते हैं।

विषय पर पाठ और प्रस्तुति: "वर्गमूल फ़ंक्शन का ग्राफ़। परिभाषा का क्षेत्र और ग्राफ़ का निर्माण"

अतिरिक्त सामग्री
प्रिय उपयोगकर्ताओं, अपनी टिप्पणियाँ, समीक्षाएँ, शुभकामनाएँ छोड़ना न भूलें। सभी सामग्रियों की जांच एंटी-वायरस प्रोग्राम द्वारा की गई है।

ग्रेड 8 के लिए इंटीग्रल ऑनलाइन स्टोर में शैक्षिक सहायता और सिमुलेटर
मोर्दकोविच ए.जी. द्वारा पाठ्यपुस्तक के लिए इलेक्ट्रॉनिक पाठ्यपुस्तक।
आठवीं कक्षा के लिए इलेक्ट्रॉनिक बीजगणित कार्यपुस्तिका

वर्गमूल फ़ंक्शन का ग्राफ़

दोस्तों, हम पहले ही फ़ंक्शंस के ग्राफ़ बनाते हुए एक से अधिक बार मिल चुके हैं। हमने कई रैखिक कार्यों का निर्माण किया और परवलय. सामान्य तौर पर, किसी भी फ़ंक्शन को $y=f(x)$ के रूप में लिखना सुविधाजनक होता है। यह दो चर वाला एक समीकरण है - x के प्रत्येक मान के लिए हमें y मिलता है। कुछ दिए गए ऑपरेशन f निष्पादित करने के बाद, हम सभी संभावित x के सेट को सेट y पर मैप करते हैं। हम लगभग किसी भी गणितीय संक्रिया को फलन f के रूप में लिख सकते हैं।

आमतौर पर, फ़ंक्शन प्लॉट करते समय, हम एक तालिका का उपयोग करते हैं जिसमें हम x और y के मान रिकॉर्ड करते हैं। उदाहरण के लिए, फ़ंक्शन $y=5x^2$ के लिए निम्नलिखित तालिका का उपयोग करना सुविधाजनक है: कार्टेशियन समन्वय प्रणाली पर परिणामी बिंदुओं को चिह्नित करें और ध्यान से उन्हें एक चिकनी वक्र से कनेक्ट करें। हमारा कार्य सीमित नहीं है. केवल इन बिंदुओं के साथ हम परिभाषा के दिए गए क्षेत्र से बिल्कुल किसी भी मूल्य x को प्रतिस्थापित कर सकते हैं, अर्थात, वे x जिनके लिए अभिव्यक्ति समझ में आती है।

पिछले पाठों में से एक में हमने एक नया निष्कर्षण ऑपरेशन सीखा वर्गमूल. प्रश्न उठता है: क्या हम इस ऑपरेशन का उपयोग करके किसी फ़ंक्शन को परिभाषित कर सकते हैं और उसका ग्राफ़ बना सकते हैं? आइए फ़ंक्शन $y=f(x)$ के सामान्य रूप का उपयोग करें। आइए y और x को उनके स्थान पर छोड़ दें, और f के बजाय हम वर्गमूल संक्रिया प्रस्तुत करते हैं: $y=\sqrt(x)$।
गणितीय संक्रिया को जानने के बाद, हम फ़ंक्शन को परिभाषित करने में सक्षम थे।

वर्गमूल फलन का रेखांकन

आइए इस फ़ंक्शन का ग्राफ़ बनाएं। वर्गमूल की परिभाषा के आधार पर, हम इसकी गणना केवल गैर-नकारात्मक संख्याओं, यानी $x≥0$ से कर सकते हैं।
आइए एक तालिका बनाएं:
आइए निर्देशांक तल पर अपने बिंदु अंकित करें।

हमें बस परिणामी बिंदुओं को सावधानीपूर्वक जोड़ना है।

दोस्तों, ध्यान दें: यदि हमारे फ़ंक्शन के ग्राफ़ को उसकी तरफ घुमाया जाए, तो हमें परवलय की बाईं शाखा मिलती है। वास्तव में, यदि मानों की तालिका में पंक्तियों की अदला-बदली की जाती है (शीर्ष पंक्ति को नीचे से), तो हमें केवल परवलय के लिए मान प्राप्त होते हैं।

फ़ंक्शन का डोमेन $y=\sqrt(x)$

किसी फ़ंक्शन के ग्राफ़ का उपयोग करके, गुणों का वर्णन करना काफी आसान है।
1. परिभाषा का दायरा: $$.
बी) $$.

समाधान।
हम अपने उदाहरण को दो तरीकों से हल कर सकते हैं। प्रत्येक पत्र में हम विभिन्न विधियों का वर्णन करेंगे।

ए) आइए ऊपर निर्मित फ़ंक्शन के ग्राफ़ पर लौटें और सेगमेंट के आवश्यक बिंदुओं को चिह्नित करें। यह स्पष्ट रूप से देखा गया है कि $x=9$ के लिए फ़ंक्शन अन्य सभी मानों से बड़ा है। इसका मतलब यह है कि इस बिंदु पर यह अपने उच्चतम मूल्य पर पहुँच जाता है। जब $x=4$ फ़ंक्शन का मान अन्य सभी बिंदुओं से कम होता है, जिसका अर्थ है कि यह सबसे छोटा मान है।

$y_(अधिकांश)=\sqrt(9)=3$, $y_(अधिकांश)=\sqrt(4)=2$.

बी) हम जानते हैं कि हमारा कार्य बढ़ रहा है। इसका मतलब यह है कि प्रत्येक बड़ा तर्क मान एक बड़े फ़ंक्शन मान से मेल खाता है। उच्चतम और निम्नतम मान खंड के अंत में प्राप्त किए जाते हैं:

$y_(अधिकांश)=\sqrt(11)$, $y_(अधिकांश)=\sqrt(2)$.

उदाहरण 2.
प्रश्न हल करें:

$\sqrt(x)=12-x$.

समाधान।
सबसे आसान तरीका है किसी फ़ंक्शन के दो ग्राफ़ बनाना और उनका प्रतिच्छेदन बिंदु ढूंढना।
निर्देशांक $(9;3)$ के साथ प्रतिच्छेदन बिंदु ग्राफ़ पर स्पष्ट रूप से दिखाई देता है। इसका मतलब है कि $x=9$ हमारे समीकरण का समाधान है।
उत्तर: $x=9$.

दोस्तों, क्या हम आश्वस्त हो सकते हैं कि इस उदाहरण का कोई और समाधान नहीं है? एक कार्य बढ़ता है, दूसरा घटता है। सामान्य तौर पर, उनमें या तो उभयनिष्ठ बिंदु नहीं होते या केवल एक पर ही प्रतिच्छेद करते हैं।

उदाहरण 3.

फ़ंक्शन का ग्राफ़ बनाएं और पढ़ें:

$\begin (केस) -x, x 9. \end (केस)$

हमें फ़ंक्शन के तीन आंशिक ग्राफ़ बनाने की ज़रूरत है, प्रत्येक अपने स्वयं के अंतराल पर।

आइए हमारे फ़ंक्शन के गुणों का वर्णन करें:
1. परिभाषा का क्षेत्र: $(-∞;+∞)$.
2. $x=0$ और $x=12$ के लिए $y=0$; $у>0$ के लिए $хϵ(-∞;12)$; $y 3. फ़ंक्शन अंतराल $(-∞;0)U(9;+∞)$ पर घटता है। फ़ंक्शन अंतराल $(0;9)$ पर बढ़ रहा है।
4. फ़ंक्शन परिभाषा के संपूर्ण क्षेत्र में निरंतर है।
5. कोई अधिकतम या न्यूनतम मूल्य नहीं है.
6. मानों की सीमा: $(-∞;+∞)$.

स्वतंत्र रूप से हल करने योग्य समस्याएं

1. खंड पर वर्गमूल फ़ंक्शन का सबसे बड़ा और सबसे छोटा मान ज्ञात करें:
ए) $$;
बी) $$.
2. समीकरण हल करें: $\sqrt(x)=30-x$.
3. फ़ंक्शन का ग्राफ बनाएं और पढ़ें: $\begin (केस) 2-x, x 4. \end (केस)$
4. फ़ंक्शन का ग्राफ़ बनाएं और पढ़ें: $y=\sqrt(-x)$।

फेसबुक

ट्विटर

के साथ संपर्क में

सहपाठियों

गूगल +