Logaritam broja 8 do baze 4. Šta je logaritam. Kako napisati broj kao logaritam

Očuvanje vaše privatnosti nam je važno. Iz tog razloga smo razvili Politiku privatnosti koja opisuje kako koristimo i pohranjujemo vaše podatke. Pregledajte našu praksu privatnosti i javite nam ako imate pitanja.

Prikupljanje i korištenje ličnih podataka

Lični podaci odnose se na podatke koji se mogu koristiti za identifikaciju ili kontaktiranje određene osobe.

Od vas se može tražiti da unesete svoje lične podatke u bilo koje vrijeme kada nas kontaktirate.

U nastavku su navedeni neki primjeri vrsta ličnih podataka koje možemo prikupljati i kako ih možemo koristiti.

Koje lične podatke prikupljamo:

• Kada podnesete prijavu na stranici, možemo prikupiti različite informacije, uključujući vaše ime, broj telefona, adresu e-pošte itd.

Kako koristimo vaše lične podatke:

• Lični podaci koje prikupljamo omogućavaju nam da vas kontaktiramo s jedinstvenim ponudama, promocijama i drugim događajima i nadolazećim događajima.
• S vremena na vrijeme možemo koristiti vaše lične podatke za slanje važnih obavijesti i komunikacija.
• Lične podatke možemo koristiti i za interne svrhe, kao što su provođenje revizija, analiza podataka i različita istraživanja kako bismo poboljšali usluge koje pružamo i dali vam preporuke u vezi s našim uslugama.
• Ako učestvujete u nagradnoj igri, natjecanju ili sličnoj promociji, možemo koristiti informacije koje nam date za upravljanje takvim programima.

Otkrivanje informacija trećim licima

Podatke koje dobijemo od vas ne otkrivamo trećim licima.

Izuzeci:

• Ako je potrebno - u skladu sa zakonom, sudskim postupkom, u sudskom postupku, i/ili na osnovu javnih zahtjeva ili zahtjeva državnih organa u Ruskoj Federaciji - otkriti vaše lične podatke. Takođe možemo otkriti informacije o vama ako utvrdimo da je takvo otkrivanje neophodno ili prikladno za sigurnosne, provođenje zakona ili druge svrhe od javnog značaja.
• U slučaju reorganizacije, spajanja ili prodaje, možemo prenijeti lične podatke koje prikupimo na odgovarajuću treću stranu.

Zaštita ličnih podataka

Poduzimamo mjere opreza - uključujući administrativne, tehničke i fizičke - da zaštitimo vaše osobne podatke od gubitka, krađe i zloupotrebe, kao i neovlaštenog pristupa, otkrivanja, izmjene i uništenja.

Poštivanje vaše privatnosti na nivou kompanije

Kako bismo osigurali da su vaši lični podaci sigurni, našim zaposlenima prenosimo standarde privatnosti i sigurnosti i striktno provodimo praksu privatnosti.

Kao što znate, kada se množe izrazi sa stepenom, njihovi eksponenti se uvijek sabiraju (a b *a c = a b+c). Ovaj matematički zakon je izveo Arhimed, a kasnije, u 8. veku, matematičar Virasen je napravio tabelu celobrojnih eksponenata. Upravo su oni poslužili za dalje otkrivanje logaritama. Primjeri korištenja ove funkcije mogu se naći gotovo svugdje gdje trebate pojednostaviti glomazno množenje jednostavnim sabiranjem. Ako odvojite 10 minuta čitajući ovaj članak, objasnit ćemo vam što su logaritmi i kako s njima raditi. Jednostavnim i pristupačnim jezikom.

Definicija u matematici

Logaritam je izraz sljedećeg oblika: log a b=c, to jest, logaritam bilo kojeg nenegativnog broja (tj. bilo kojeg pozitivnog) “b” na njegovu bazu “a” smatra se stepenom “c ” na koju se baza “a” mora podići da bi se na kraju dobila vrijednost “b”. Analizirajmo logaritam na primjerima, recimo da postoji izraz log 2 8. Kako pronaći odgovor? Vrlo je jednostavno, potrebno je pronaći takvu snagu da od 2 do tražene snage dobijete 8. Nakon nekih proračuna u glavi, dobijamo broj 3! I to je tačno, jer 2 na stepen od 3 daje odgovor kao 8.

Vrste logaritama

Za mnoge učenike i studente ova se tema čini komplikovanom i nerazumljivom, ali zapravo logaritmi nisu toliko strašni, najvažnije je razumjeti njihovo općenito značenje i zapamtiti njihova svojstva i neka pravila. Postoje tri odvojene vrste logaritamskih izraza:

1. Prirodni logaritam ln a, gdje je baza Ojlerov broj (e = 2,7).
2. Decimala a, gdje je osnova 10.
3. Logaritam bilo kojeg broja b na osnovu a>1.

Svaki od njih se rješava na standardni način, uključujući pojednostavljenje, redukciju i naknadno svođenje na jedan logaritam korištenjem logaritamskih teorema. Da biste dobili ispravne vrijednosti logaritama, trebali biste zapamtiti njihova svojstva i redoslijed radnji prilikom njihovog rješavanja.

Pravila i neka ograničenja

U matematici postoji nekoliko pravila-ograničenja koja su prihvaćena kao aksiom, odnosno nisu predmet rasprave i predstavljaju istinu. Na primjer, nemoguće je podijeliti brojeve sa nulom, a također je nemoguće izdvojiti paran korijen negativnih brojeva. Logaritmi također imaju svoja pravila, slijedeći koja možete lako naučiti raditi čak i sa dugim i prostranim logaritamskim izrazima:

• Osnova “a” uvijek mora biti veća od nule, a ne jednaka 1, inače će izraz izgubiti svoje značenje, jer su “1” i “0” u bilo kojem stepenu uvijek jednaki njihovim vrijednostima;
• ako je a > 0, onda a b > 0, ispada da “c” takođe mora biti veće od nule.

Kako riješiti logaritme?

Na primjer, daje se zadatak pronaći odgovor na jednadžbu 10 x = 100. Ovo je vrlo lako, potrebno je odabrati stepen podizanjem broja deset na koji dobijamo 100. Ovo je, naravno, 10 2 = 100.

Sada predstavimo ovaj izraz u logaritamskom obliku. Dobijamo log 10 100 = 2. Prilikom rješavanja logaritma, sve radnje se praktično konvergiraju da bi se pronašla potencija na koju je potrebno unijeti bazu logaritma da bi se dobio dati broj.

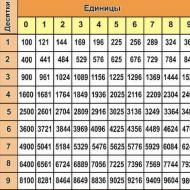
Da biste precizno odredili vrijednost nepoznatog stepena, morate naučiti kako raditi s tablicom stupnjeva. izgleda ovako:

Kao što vidite, neki eksponenti se mogu pogoditi intuitivno ako imate tehnički um i poznavanje tablice množenja. Međutim, za veće vrijednosti trebat će vam stol za napajanje. Mogu ga koristiti čak i oni koji ne znaju ništa o složenim matematičkim temama. Lijeva kolona sadrži brojeve (osnova a), gornji red brojeva je vrijednost stepena c na koji je broj a podignut. Na raskrsnici ćelije sadrže brojčane vrijednosti koje su odgovor (a c =b). Uzmimo, na primjer, prvu ćeliju sa brojem 10 i kvadriramo je, dobićemo vrijednost 100, koja je naznačena na sjecištu naše dvije ćelije. Sve je tako jednostavno i lako da će i najistinskiji humanista razumjeti!

Jednačine i nejednačine

Ispada da je pod određenim uslovima eksponent logaritam. Stoga se bilo koji matematički numerički izrazi može zapisati kao logaritamska jednakost. Na primjer, 3 4 =81 se može napisati kao logaritam 81 na bazi 3 jednak četiri (log 3 81 = 4). Za negativne potencije pravila su ista: 2 -5 = 1/32 zapišemo to kao logaritam, dobijemo log 2 (1/32) = -5. Jedna od najfascinantnijih sekcija matematike je tema "logaritma". U nastavku ćemo pogledati primjere i rješenja jednadžbi, odmah nakon proučavanja njihovih svojstava. Pogledajmo sada kako izgledaju nejednakosti i kako ih razlikovati od jednačina.

Dat je sljedeći izraz: log 2 (x-1) > 3 - to je logaritamska nejednakost, jer je nepoznata vrijednost “x” ispod logaritamskog predznaka. I u izrazu se upoređuju dvije veličine: logaritam željenog broja prema bazi dva je veći od broja tri.

Najvažnija razlika između logaritamskih jednadžbi i nejednačina je u tome što jednadžbe sa logaritmima (na primjer, logaritam 2 x = √9) podrazumijevaju jednu ili više specifičnih brojčanih vrijednosti u odgovoru, dok se pri rješavanju nejednadžbe uzimaju i raspon prihvatljivih vrijednosti ​​i tačke se određuju kršenjem ove funkcije. Kao posljedica toga, odgovor nije jednostavan skup pojedinačnih brojeva, kao u odgovoru na jednadžbu, već kontinuirani niz ili skup brojeva.

Osnovne teoreme o logaritmima

Prilikom rješavanja primitivnih zadataka pronalaženja vrijednosti logaritma, njegova svojstva možda neće biti poznata. Međutim, kada su u pitanju logaritamske jednačine ili nejednačine, prije svega, potrebno je jasno razumjeti i primijeniti u praksi sva osnovna svojstva logaritama. Kasnije ćemo pogledati primjere jednadžbi; hajde da prvo pogledamo svako svojstvo detaljnije.

1. Glavni identitet izgleda ovako: a logaB =B. Primjenjuje se samo kada je a veće od 0, nije jednako jedan, a B je veće od nule.
2. Logaritam proizvoda se može predstaviti sljedećom formulom: log d (s 1 * s 2) = log d s 1 + log d s 2. U ovom slučaju, obavezan uslov je: d, s 1 i s 2 > 0; a≠1. Možete dati dokaz za ovu logaritamsku formulu, sa primjerima i rješenjem. Neka log a s 1 = f 1 i log a s 2 = f 2, tada a f1 = s 1, a f2 = s 2. Dobijamo da je s 1 * s 2 = a f1 *a f2 = a f1+f2 (osobine stepeni ), a zatim po definiciji: log a (s 1 * s 2) = f 1 + f 2 = log a s1 + log a s 2, što je trebalo dokazati.
3. Logaritam količnika izgleda ovako: log a (s 1/s 2) = log a s 1 - log a s 2.
4. Teorema u obliku formule ima sljedeći oblik: log a q b n = n/q log a b.

Ova formula se naziva “svojstvo stepena logaritma”. Podsjeća na svojstva običnih stupnjeva, i nije iznenađujuće, jer se sva matematika zasniva na prirodnim postulatima. Pogledajmo dokaz.

Neka log a b = t, ispada da je a t = b. Ako oba dijela podignemo na stepen m: a tn = b n ;

ali pošto je a tn = (a q) nt/q = b n, dakle log a q b n = (n*t)/t, onda log a q b n = n/q log a b. Teorema je dokazana.

Primjeri problema i nejednakosti

Najčešći tipovi zadataka o logaritmima su primjeri jednačina i nejednačina. Nalaze se u gotovo svim knjigama zadataka, a također su obavezan dio ispita iz matematike. Da biste ušli na fakultet ili položili prijemne ispite iz matematike, morate znati kako pravilno riješiti takve zadatke.

Nažalost, ne postoji jedinstveni plan ili shema za rješavanje i određivanje nepoznate vrijednosti logaritma, ali se određena pravila mogu primijeniti na svaku matematičku nejednačinu ili logaritamsku jednačinu. Prije svega, trebali biste saznati da li se izraz može pojednostaviti ili svesti na opći oblik. Duge logaritamske izraze možete pojednostaviti ako pravilno koristite njihova svojstva. Hajde da ih brzo upoznamo.

Prilikom rješavanja logaritamskih jednadžbi moramo odrediti koji tip logaritma imamo: primjer izraza može sadržavati prirodni logaritam ili decimalni.

Evo primjera ln100, ln1026. Njihovo rješenje se svodi na činjenicu da treba odrediti snagu kojoj će baza 10 biti jednaka 100 i 1026, respektivno. Da biste riješili prirodne logaritme, morate primijeniti logaritamske identitete ili njihova svojstva. Pogledajmo primjere rješavanja logaritamskih problema različitih tipova.

Kako koristiti logaritamske formule: s primjerima i rješenjima

Dakle, pogledajmo primjere korištenja osnovnih teorema o logaritmima.

1. Svojstvo logaritma proizvoda može se koristiti u zadacima gdje je potrebno rastaviti veliku vrijednost broja b na jednostavnije faktore. Na primjer, log 2 4 + log 2 128 = log 2 (4*128) = log 2 512. Odgovor je 9.
2. log 4 8 = log 2 2 2 3 = 3/2 log 2 2 = 1,5 - kao što vidite, koristeći četvrto svojstvo stepena logaritma, uspjeli smo riješiti naizgled složen i nerješiv izraz. Vi samo trebate faktorisati bazu, a zatim izvući vrijednosti eksponenta iz predznaka logaritma.

Zadaci sa Jedinstvenog državnog ispita

Logaritmi se često nalaze na prijemnim ispitima, posebno mnogi logaritamski problemi na Jedinstvenom državnom ispitu (državni ispit za sve maturante). Obično su ovi zadaci prisutni ne samo u dijelu A (najlakši dio ispita), već i u dijelu C (najsloženiji i najobimniji zadaci). Ispit zahtijeva tačno i savršeno poznavanje teme „Prirodni logaritmi“.

Primjeri i rješenja problema preuzeti su iz službenih verzija Jedinstvenog državnog ispita. Pogledajmo kako se takvi zadaci rješavaju.

Dat log 2 (2x-1) = 4. Rješenje:
prepišimo izraz, pojednostavljujući ga malo log 2 (2x-1) = 2 2, po definiciji logaritma dobijamo da je 2x-1 = 2 4, dakle 2x = 17; x = 8,5.

• Najbolje je sve logaritme svesti na istu bazu kako rješenje ne bi bilo glomazno i ​​zbunjujuće.
• Svi izrazi pod predznakom logaritma su označeni kao pozitivni, stoga, kada se eksponent izraza koji je pod predznakom logaritma i kao njegova baza izvadi kao množitelj, izraz koji ostaje pod logaritmom mora biti pozitivan.

\(a^(b)=c\) \(\Strelica ulevo\) \(\log_(a)(c)=b\)

Hajde da to jednostavnije objasnimo. Na primjer, \(\log_(2)(8)\) je jednako potenciji na koju se \(2\) mora podići da bi se dobilo \(8\). Iz ovoga je jasno da je \(\log_(2)(8)=3\).

Argument i baza logaritma

Svaki logaritam ima sljedeću "anatomiju":

Argument logaritma se obično piše na njegovom nivou, a baza se upisuje u indeksu bliže znaku logaritma. A ovaj unos glasi ovako: "logaritam od dvadeset pet do osnove pet."

Kako izračunati logaritam?

Da biste izračunali logaritam, morate odgovoriti na pitanje: na koji stepen treba podići bazu da biste dobili argument?

Na primjer, izračunajte logaritam: a) \(\log_(4)(16)\) b) \(\log_(3)\)\(\frac(1)(3)\) c) \(\log_(\ sqrt (5))(1)\) d) \(\log_(\sqrt(7))(\sqrt(7))\) e) \(\log_(3)(\sqrt(3))\)

a) Na koji stepen treba podići \(4\) da bi se dobilo \(16\)? Očigledno drugi. Zbog toga:

\(\log_(4)(16)=2\)

\(\log_(3)\)\(\frac(1)(3)\) \(=-1\)

c) Na koji stepen treba podići \(\sqrt(5)\) da bi se dobilo \(1\)? Koja moć čini bilo kojeg brojem jedan? Nula, naravno!

\(\log_(\sqrt(5))(1)=0\)

d) Na koji stepen treba podići \(\sqrt(7)\) da bi se dobio \(\sqrt(7)\)? Prvo, bilo koji broj na prvi stepen jednak je samom sebi.

\(\log_(\sqrt(7))(\sqrt(7))=1\)

e) Na koji stepen treba podići \(3\) da bi se dobio \(\sqrt(3)\)? Odatle znamo da je to razlomak, što znači da je kvadratni korijen potencija \(\frac(1)(2)\) .

\(\log_(3)(\sqrt(3))=\)\(\frac(1)(2)\)

Primjer : Izračunajte logaritam \(\log_(4\sqrt(2))(8)\)

Rješenje :

Odgovori : \(\log_(4\sqrt(2))(8)=1,2\)

Zašto je izmišljen logaritam?

Da bismo ovo razumjeli, riješimo jednačinu: \(3^(x)=9\). Samo uparite \(x\) da bi jednakost funkcionirala. Naravno, \(x=2\).

Sada riješite jednačinu: \(3^(x)=8\). Koliko je x jednako? To je poenta.

Oni najpametniji će reći: "X je malo manje od dva." Kako tačno napisati ovaj broj? Da bi se odgovorilo na ovo pitanje, izmišljen je logaritam. Zahvaljujući njemu, odgovor se ovdje može napisati kao \(x=\log_(3)(8)\).

Želim da naglasim da \(\log_(3)(8)\), kao svaki logaritam je samo broj. Da, izgleda neobično, ali je kratak. Jer ako bismo to htjeli zapisati kao decimalu, to bi izgledalo ovako: \(1.892789260714.....\)

Primjer : Riješite jednačinu \(4^(5x-4)=10\)

Rješenje :

Odgovori : \(\frac(\log_(4)(10)+4)(5)\)

Decimalni i prirodni logaritmi

Kao što je navedeno u definiciji logaritma, njegova baza može biti bilo koji pozitivan broj osim jednog \((a>0, a\neq1)\). A među svim mogućim bazama, postoje dvije koje se tako često javljaju da je izmišljen poseban kratki zapis za logaritme s njima:

Prirodni logaritam: logaritam čija je osnova Ojlerov broj \(e\) (jednak približno \(2,7182818…\)), a logaritam je zapisan kao \(\ln(a)\).

To je, \(\ln(a)\) je isto što i \(\log_(e)(a)\)

Decimalni logaritam: Logaritam čija je baza 10 piše se \(\lg(a)\).

To je, \(\lg(a)\) je isto što i \(\log_(10)(a)\), gdje je \(a\) neki broj.

Osnovni logaritamski identitet

Logaritmi imaju mnoga svojstva. Jedan od njih se zove "Osnovni logaritamski identitet" i izgleda ovako:

Ovo svojstvo slijedi direktno iz definicije. Pogledajmo kako je tačno nastala ova formula.

Prisjetimo se kratke notacije definicije logaritma:

ako je \(a^(b)=c\), onda \(\log_(a)(c)=b\)

To jest, \(b\) je isto što i \(\log_(a)(c)\). Tada možemo napisati \(\log_(a)(c)\) umjesto \(b\) u formuli \(a^(b)=c\). Ispostavilo se \(a^(\log_(a)(c))=c\) - glavni logaritamski identitet.

Možete pronaći i druga svojstva logaritama. Uz njihovu pomoć možete pojednostaviti i izračunati vrijednosti izraza logaritmima, koje je teško izravno izračunati.

Primjer : Pronađite vrijednost izraza \(36^(\log_(6)(5))\)

Rješenje :

Odgovori : \(25\)

Kako napisati broj kao logaritam?

Kao što je gore spomenuto, svaki logaritam je samo broj. I obrnuto: bilo koji broj se može napisati kao logaritam. Na primjer, znamo da je \(\log_(2)(4)\) jednako dva. Tada umjesto dva možete napisati \(\log_(2)(4)\).

Ali \(\log_(3)(9)\) je također jednako \(2\), što znači da možemo napisati i \(2=\log_(3)(9)\) . Isto tako sa \(\log_(5)(25)\), i sa \(\log_(9)(81)\), itd. Odnosno, ispostavilo se

\(2=\log_(2)(4)=\log_(3)(9)=\log_(4)(16)=\log_(5)(25)=\log_(6)(36)=\ log_(7)(49)...\)

Dakle, ako trebamo, možemo napisati dva kao logaritam sa bilo kojom bazom bilo gdje (bilo u jednadžbi, u izrazu ili u nejednadžbi) - jednostavno zapišemo bazu na kvadrat kao argument.

Isto je i sa trojkom – može se napisati kao \(\log_(2)(8)\), ili kao \(\log_(3)(27)\), ili kao \(\log_(4)( 64) \)... Ovdje upisujemo bazu u kocki kao argument:

\(3=\log_(2)(8)=\log_(3)(27)=\log_(4)(64)=\log_(5)(125)=\log_(6)(216)=\ log_(7)(343)...\)

I sa četiri:

\(4=\log_(2)(16)=\log_(3)(81)=\log_(4)(256)=\log_(5)(625)=\log_(6)(1296)=\ log_(7)(2401)...\)

I sa minus jedan:

\(-1=\) \(\log_(2)\)\(\frac(1)(2)\) \(=\) \(\log_(3)\)\(\frac(1)( 3)\) \(=\) \(\log_(4)\)\(\frac(1)(4)\) \(=\) \(\log_(5)\)\(\frac(1) )(5)\) \(=\) \(\log_(6)\)\(\frac(1)(6)\) \(=\) \(\log_(7)\)\(\frac (1)(7)\) \(...\)

I sa jednom trećinom:

\(\frac(1)(3)\) \(=\log_(2)(\sqrt(2))=\log_(3)(\sqrt(3))=\log_(4)(\sqrt( 4))=\log_(5)(\sqrt(5))=\log_(6)(\sqrt(6))=\log_(7)(\sqrt(7))...\)

Bilo koji broj \(a\) može se predstaviti kao logaritam sa bazom \(b\): \(a=\log_(b)(b^(a))\)

Primjer : Pronađite značenje izraza \(\frac(\log_(2)(14))(1+\log_(2)(7))\)

Rješenje :

Odgovori : \(1\)

Logaritam datog broja naziva se eksponent na koji se drugi broj mora podići, pozvati osnovu logaritam da dobijete ovaj broj. Na primjer, logaritam baze 10 od 100 je 2. Drugim riječima, 10 mora biti na kvadrat da bi se dobilo 100 (10 2 = 100). Ako n– dati broj, b– baza i l– logaritam, dakle b l = n. Broj n naziva se i bazni antilogaritam b brojevi l. Na primjer, antilogaritam od 2 prema bazi 10 jednak je 100. Ovo se može zapisati u obliku dnevnika odnosa b n = l i antilog b l = n.

Osnovna svojstva logaritama:

Bilo koji pozitivan broj osim jedan može poslužiti kao osnova za logaritme, ali nažalost ispada da ako b I n su racionalni brojevi, onda u rijetkim slučajevima postoji takav racionalni broj l, Šta b l = n. Međutim, moguće je definirati iracionalan broj l, na primjer, takav da je 10 l= 2; ovo je iracionalan broj l može se aproksimirati sa bilo kojom traženom tačnošću racionalnim brojevima. Ispada da je u datom primjeru l je približno jednako 0,3010, a ova aproksimacija logaritma od 2 baze 10 može se naći u četverocifrenim tablicama decimalnih logaritama. Logaritmi s bazom 10 (ili logaritmi s bazom 10) se toliko često koriste u proračunima da se nazivaju običan logaritma i zapisano kao log2 = 0,3010 ili log2 = 0,3010, izostavljajući eksplicitnu naznaku osnove logaritma. Logaritmi bazi e, transcendentalni broj približno jednak 2,71828, nazivaju se prirodno logaritmi. Nalaze se uglavnom u radovima o matematičkoj analizi i njenoj primjeni na različite nauke. Prirodni logaritmi se također pišu bez eksplicitne naznake baze, već uz korištenje posebne oznake ln: na primjer, ln2 = 0,6931, jer e 0,6931 = 2.

Korištenje tablica običnih logaritama.

Regularni logaritam broja je eksponent na koji se mora podići 10 da bi se dobio dati broj. Pošto je 10 0 = 1, 10 1 = 10 i 10 2 = 100, odmah dobijamo da je log1 = 0, log10 = 1, log100 = 2, itd. za povećanje cjelobrojnih potencija 10. Isto tako, 10 –1 = 0,1, 10 –2 = 0,01 i stoga log0,1 = –1, log0,01 = –2, itd. za sve negativne cjelobrojne potencije 10. Uobičajeni logaritmi preostalih brojeva su zatvoreni između logaritama najbližih cijelih potencija od 10; log2 mora biti između 0 i 1, log20 mora biti između 1 i 2, a log0.2 mora biti između -1 i 0. Dakle, logaritam se sastoji od dva dijela, cijelog broja i decimale, zatvorenih između 0 i 1. zove se cijeli broj karakteristika logaritam i određen je samim brojem, naziva se razlomak mantissa i može se pronaći iz tabela. Takođe, log20 = log(2´10) = log2 + log10 = (log2) + 1. Logaritam od 2 je 0,3010, tako da je log20 = 0,3010 + 1 = 1,3010. Slično, log0.2 = log(2o10) = log2 – log10 = (log2) – 1 = 0.3010 – 1. Nakon oduzimanja dobijamo log0.2 = – 0.6990. Međutim, zgodnije je predstaviti log0,2 kao 0,3010 – 1 ili kao 9,3010 – 10; Može se formulisati i opšte pravilo: svi brojevi dobijeni iz datog broja množenjem sa stepenom od 10 imaju identične mantise jednake mantisi datog broja. Većina tabela prikazuje mantise brojeva u rasponu od 1 do 10, jer se mantise svih ostalih brojeva mogu dobiti iz onih navedenih u tabeli.

Većina tabela daje logaritme sa četiri ili pet decimalnih mesta, iako postoje tabele sa sedam cifara i tabele sa čak i više decimalnih mesta. Najlakši način da naučite kako koristiti takve tablice je pomoću primjera. Da bismo pronašli log3.59, prije svega, napominjemo da je broj 3.59 između 10 0 i 10 1, pa je njegova karakteristika 0. Pronalazimo broj 35 (lijevo) u tabeli i krećemo se duž reda do kolona koja ima broj 9 na vrhu; presjek ove kolone i reda 35 je 5551, tako da je log3.59 = 0.5551. Da biste pronašli mantisu broja sa četiri značajne cifre, morate koristiti interpolaciju. U nekim tabelama, interpolacija je olakšana proporcijama datim u zadnjih devet kolona na desnoj strani svake stranice tabela. Nađimo sada log736.4; broj 736.4 leži između 10 2 i 10 3, pa je karakteristika njegovog logaritma 2. U tabeli nalazimo red sa leve strane od kojeg se nalazi 73 i kolona 6. Na preseku ovog reda i ove kolone nalazi se broj 8669. Među linearnim dijelovima nalazimo kolonu 4. Na sjecištu reda 73 i kolone 4 nalazi se broj 2. Dodavanjem 2 na 8669, dobijamo mantisu - jednaka je 8671. Dakle, log736.4 = 2.8671.

Prirodni logaritmi.

Tablice i svojstva prirodnih logaritama su slične tablicama i svojstvima običnih logaritama. Glavna razlika između jednog i drugog je u tome što cijeli broj prirodnog logaritma nije značajan u određivanju položaja decimalne točke, te stoga razlika između mantise i karakteristike ne igra posebnu ulogu. Prirodni logaritmi brojeva 5.432; 54,32 i 543,2 jednaki su 1,6923, respektivno; 3,9949 i 6,2975. Odnos između ovih logaritama će postati očigledan ako uzmemo u obzir razlike između njih: log543.2 – log54.32 = 6.2975 – 3.9949 = 2.3026; posljednji broj nije ništa drugo do prirodni logaritam broja 10 (napisan ovako: ln10); log543,2 – log5,432 = 4,6052; posljednji broj je 2ln10. Ali 543,2 = 10´54,32 = 10 2´5,432. Dakle, prirodnim logaritmom datog broja a možete pronaći prirodne logaritme brojeva jednake umnošku broja a za bilo koji stepen n brojevi 10 ako na ln a dodati ln10 pomnoženo sa n, tj. ln( aґ10n) = log a + n ln10 = ln a + 2,3026n. Na primjer, ln0,005432 = ln(5,432´10 –3) = ln5,432 – 3ln10 = 1,6923 – (3´2,3026) = – 5,2155. Stoga tablice prirodnih logaritama, kao i tablice običnih logaritama, obično sadrže samo logaritme brojeva od 1 do 10. U sistemu prirodnih logaritama može se govoriti o antilogaritmima, ali češće govore o eksponencijalnoj funkciji ili eksponentu. Ako x= log y, To y = e x, And y naziva eksponentom x(radi tipografske pogodnosti, oni često pišu y= exp x). Eksponent igra ulogu antilogaritma broja x.

Koristeći tablice decimalnih i prirodnih logaritama, možete kreirati tablice logaritama u bilo kojoj osnovi osim 10 i e. Ako log b a = x, To b x = a, i stoga log c b x=log c a ili x log c b=log c a, ili x=log c a/log c b=log b a. Stoga, koristeći ovu formulu inverzije iz tabele baznog logaritma c možete napraviti tablice logaritama u bilo kojoj drugoj bazi b. Množilac 1/log c b pozvao prelazni modul iz baze c do baze b. Ništa ne sprječava, na primjer, korištenje formule inverzije ili prijelaz iz jednog sistema logaritama u drugi, pronalaženje prirodnih logaritama iz tablice običnih logaritama ili obrnuti prijelaz. Na primjer, log105.432 = log e 5.432/log e 10 = 1,6923/2,3026 = 1,6923´0,4343 = 0,7350. Broj 0,4343, kojim se prirodni logaritam datog broja mora pomnožiti da bi se dobio običan logaritam, modul je prelaska na sistem običnih logaritama.

Specijalni stolovi.

Logaritmi su prvobitno izmišljeni tako da, koristeći svoja svojstva log ab=log a+ log b i log a/b=log a–log b, pretvaraju proizvode u zbrojeve, a količnike u razlike. Drugim riječima, ako log a i log b su poznati, onda pomoću sabiranja i oduzimanja lako možemo pronaći logaritam proizvoda i količnika. U astronomiji se, međutim, često daju vrijednosti log a i log b treba pronaći dnevnik ( a + b) ili log( a – b). Naravno, prvo se može pronaći iz tablica logaritama a I b, zatim izvršite naznačeno sabiranje ili oduzimanje i, ponovo pozivajući se na tabele, pronađite tražene logaritme, ali takav postupak bi zahtijevao pozivanje na tabele tri puta. Z. Leonelli je 1802. objavio tabele tzv. Gaussovi logaritmi– logaritmi za sabiranje zbira i razlika – koji su omogućili da se ograničimo na jedan pristup tabelama.

I. Kepler je 1624. godine predložio tablice proporcionalnih logaritama, tj. logaritmi brojeva a/x, Gdje a– neka pozitivna konstantna vrijednost. Ove tabele koriste prvenstveno astronomi i navigatori.

Proporcionalni logaritmi pri a= 1 se pozivaju koloritmi i koriste se u proračunima kada se radi o proizvodima i količnikima. Kologaritam broja n jednak logaritmu recipročnog broja; one. colog n= log1/ n= – log n. Ako je log2 = 0,3010, onda je colog2 = – 0,3010 = 0,6990 – 1. Prednost korištenja kolobaritama je u tome što se pri izračunavanju vrijednosti logaritma izraza kao pq/r trostruki zbir pozitivnih decimala log str+ log q+colog r lakše je pronaći nego mješoviti zapisnik sume i razlike str+ log q–log r.

Priča.

Princip koji leži u osnovi bilo kog sistema logaritama poznat je veoma dugo i može se pratiti do drevne vavilonske matematike (oko 2000. godine pne). U to vrijeme za izračunavanje složene kamate korištena je interpolacija između tabličnih vrijednosti pozitivnih cjelobrojnih potencija cijelih brojeva. Mnogo kasnije, Arhimed (287–212 pne) je koristio moći od 108 da pronađe gornju granicu broja zrna pijeska potrebnih da se u potpunosti ispuni tada poznati Univerzum. Arhimed je skrenuo pažnju na svojstvo eksponenata koje je u osnovi efektivnosti logaritama: proizvod stepena odgovara zbiru eksponenata. Krajem srednjeg vijeka i početkom moderne ere, matematičari su se sve više počeli okretati odnosu između geometrijske i aritmetičke progresije. M. Stiefel u svom eseju Integer Arithmetic(1544) dao je tablicu pozitivnih i negativnih potencija broja 2:

Stiefel je primijetio da je zbir dva broja u prvom redu (red eksponenta) jednak eksponentu dva koji odgovara proizvodu dva odgovarajuća broja u donjem redu (red eksponenta). U vezi sa ovom tabelom, Stiefel je formulisao četiri pravila koja su ekvivalentna četiri moderna pravila za operacije nad eksponentima ili četiri pravila za operacije nad logaritmima: zbir u gornjoj liniji odgovara proizvodu u donjem redu; oduzimanje na gornjoj liniji odgovara podjeli na donjoj liniji; množenje na gornjoj liniji odgovara eksponencijaciji u donjoj liniji; podjela na gornjoj liniji odgovara ukorjenjivanju na donjoj liniji.

Očigledno, pravila slična Stiefelovim pravilima navela su J. Napera da formalno uvede prvi sistem logaritama u svom radu Opis nevjerovatne tablice logaritama, objavljen 1614. Ali Napierove misli bile su zaokupljene problemom pretvaranja proizvoda u sume otkako je, više od deset godina prije objavljivanja svog rada, Napier dobio vijest iz Danske da su u opservatoriji Tycho Brahe njegovi pomoćnici imali metodu koja moguće je pretvoriti proizvode u sume. Metoda o kojoj se govori u poruci koju je Napier primio temeljila se na korištenju trigonometrijskih formula kao što su

stoga su se Naperove tablice uglavnom sastojale od logaritama trigonometrijskih funkcija. Iako koncept baze nije eksplicitno uključen u definiciju koju je predložio Napier, ulogu ekvivalentnu bazi sistema logaritama u njegovom sistemu imao je broj (1 – 10 –7)´10 7, približno jednak 1/ e.

Nezavisno od Napera i gotovo istovremeno s njim, sistem logaritama, prilično sličan tipu, izumio je i objavio J. Bürgi u Pragu, objavljen 1620. Tablice aritmetičke i geometrijske progresije. To su bile tabele antilogaritama na osnovu (1 + 10 –4) ´10 4, prilično dobra aproksimacija broja e.

U Naperovom sistemu, logaritam broja 10 7 uzet je jednak nuli, a kako su se brojevi smanjivali, logaritmi su se povećavali. Kada je G. Briggs (1561–1631) posjetio Napier, obojica su se složili da bi bilo zgodnije koristiti broj 10 kao bazu i smatrati da je logaritam jedinice nula. Zatim, kako se brojevi povećavaju, njihovi logaritmi bi se povećavali. Tako smo dobili savremeni sistem decimalnih logaritama čiju je tabelu Brigs objavio u svom radu Logaritamska aritmetika(1620). Logaritmi bazi e, iako ne baš one koje je uveo Naper, često se nazivaju Naperovim. Termine "karakteristika" i "mantisa" predložio je Briggs.

Prvi logaritmi su, iz istorijskih razloga, koristili aproksimacije brojeva 1/ e I e. Nešto kasnije, ideja o prirodnim logaritmima počela se povezivati ​​s proučavanjem područja pod hiperbolom xy= 1 (slika 1). U 17. veku pokazalo se da je površina omeđena ovom krivom osi x i ordinate x= 1 i x = a(na slici 1 ovo područje je prekriveno podebljanim i rijetkim tačkama) povećava se u aritmetičkoj progresiji kada a raste eksponencijalno. Upravo ta zavisnost se javlja u pravilima za operacije s eksponentima i logaritmima. To je dovelo do toga da se Naperijski logaritmi nazovu "hiperboličkim logaritmima".

Logaritamska funkcija.

Bilo je vremena kada su se logaritmi smatrali isključivo računskim sredstvom, ali je u 18. stoljeću, uglavnom zahvaljujući Ojlerovom radu, formiran koncept logaritamske funkcije. Grafikon takve funkcije y= log x, čije ordinate rastu u aritmetičkoj progresiji, dok apscise rastu u geometrijskoj progresiji, prikazano je na Sl. 2, A. Graf inverzne ili eksponencijalne funkcije y = e x, čije ordinate rastu u geometrijskoj progresiji, a čije apscise rastu u aritmetičkoj progresiji, prikazano je, respektivno, na Sl. 2, b. (Krive y=log x I y = 10x po obliku sličan krivinama y= log x I y = e x.) Predložene su i alternativne definicije logaritamske funkcije, npr.

kpi ; i, slično, prirodni logaritmi broja -1 su kompleksni brojevi oblika (2 k + 1)pi, Gdje k– cijeli broj. Slične tvrdnje su istinite za opšte logaritme ili druge sisteme logaritama. Dodatno, definicija logaritma se može generalizirati korištenjem Eulerovih identiteta kako bi se uključili kompleksni logaritmi kompleksnih brojeva.

Alternativna definicija logaritamske funkcije je data funkcionalnom analizom. Ako f(x) – kontinuirana funkcija realnog broja x, koji ima sljedeća tri svojstva: f (1) = 0, f (b) = 1, f (uv) = f (u) + f (v), To f(x) je definiran kao logaritam broja x na osnovu b. Ova definicija ima niz prednosti u odnosu na definiciju datu na početku ovog članka.

Prijave.

Logaritmi su se prvobitno koristili samo za pojednostavljenje proračuna, a ova aplikacija je i dalje jedna od njihovih najvažnijih. Izračunavanje proizvoda, količnika, stepena i korijena je olakšano ne samo širokom dostupnošću objavljenih tablica logaritama, već i upotrebom tzv. Slide rule - računski alat čiji se princip rada zasniva na svojstvima logaritama. Lenjir je opremljen logaritamskim skalama, tj. udaljenost od broja 1 do bilo kojeg broja x odabrano da bude jednako log x; Pomicanjem jedne skale u odnosu na drugu moguće je iscrtati zbrojeve ili razlike logaritama, što omogućava da se direktno sa skale očitaju produkti ili količniki odgovarajućih brojeva. Također možete iskoristiti prednosti predstavljanja brojeva u logaritamskom obliku. logaritamski papir za crtanje grafova (papir sa ispisanim logaritamskim skalama na obe koordinatne ose). Ako funkcija zadovoljava zakon stepena oblika y = kxn, tada njegov logaritamski graf izgleda kao prava linija, jer log y=log k + n log x– jednačina linearna u odnosu na log y i log x. Naprotiv, ako logaritamski graf neke funkcionalne zavisnosti izgleda kao prava linija, onda je ta zavisnost stepena. Semi-log papir (gdje y-osa ima logaritamsku skalu, a x-osa ima uniformnu skalu) je koristan kada trebate identificirati eksponencijalne funkcije. Jednačine oblika y = kb rx nastaju kad god se količina, kao što je populacija, količina radioaktivnog materijala ili stanje u banci, smanjuje ili povećava po stopi proporcionalnoj količini stanovništva, radioaktivnog materijala ili novca koji je trenutno dostupan. Ako se takva zavisnost nacrta na polulogaritamskom papiru, graf će izgledati kao prava linija.

Logaritamska funkcija nastaje u vezi sa širokim spektrom prirodnih oblika. Cvjetovi u cvatovima suncokreta raspoređeni su u logaritamske spirale, školjke mekušaca su uvijene Nautilus, rogove planinskih ovaca i kljunove papagaja. Svi ovi prirodni oblici mogu poslužiti kao primjeri krive poznate kao logaritamska spirala jer je u polarnom koordinatnom sistemu njena jednadžba r = ae bq, ili ln r= log a + bq. Takva kriva je opisana pokretnom tačkom, čija se udaljenost od pola povećava u geometrijskoj progresiji, a ugao opisan njenim radijus vektorom raste u aritmetičkoj progresiji. Sveprisutnost takve krivulje, a samim tim i logaritamske funkcije, dobro je ilustrirana činjenicom da se javlja u tako udaljenim i potpuno različitim područjima kao što su kontura ekscentričnog ekscentra i putanja nekih insekata koji lete prema svjetlosti.