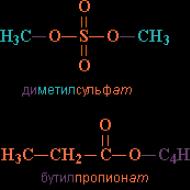
8 を底とする 4 の対数。対数とは何ですか。 数値を対数として書く方法

お客様のプライバシーを維持することは当社にとって重要です。 このため、当社はお客様の情報の使用および保管方法を説明するプライバシー ポリシーを作成しました。 当社のプライバシー慣行を確認し、ご質問がある場合はお知らせください。

個人情報の収集と利用

個人情報とは、特定の個人を識別したり連絡したりするために使用できるデータを指します。

当社にご連絡いただく際には、いつでも個人情報の提供を求められる場合があります。

以下は、当社が収集する個人情報の種類とそのような情報の使用方法の例です。

当社が収集する個人情報は次のとおりです。

• お客様がサイト上でお申し込みを送信される場合、当社はお客様のお名前、電話番号、電子メールアドレスなどを含むさまざまな情報を収集する場合があります。

お客様の個人情報の使用方法:

• 当社が収集する個人情報により、独自のオファー、プロモーション、その他のイベントや今後のイベントについてお客様にご連絡することができます。
• 当社は、重要な通知や連絡を送信するためにお客様の個人情報を使用する場合があります。
• また、当社は、当社が提供するサービスを改善し、お客様に当社のサービスに関する推奨事項を提供するために、監査、データ分析、さまざまな調査の実施などの内部目的で個人情報を使用する場合があります。
• あなたが賞品の抽選、コンテスト、または同様のプロモーションに参加する場合、当社はそのようなプログラムを管理するためにあなたが提供した情報を使用することがあります。

第三者への情報開示

当社はお客様から受け取った情報を第三者に開示することはありません。

例外:

• 法律、司法手続きに従って、および/または公的要請またはロシア連邦領域の政府当局からの要請に基づいて、必要な場合には、お客様の個人情報を開示する場合。 また、セキュリティ、法執行、またはその他の公共の重要な目的のために開示が必要または適切であると当社が判断した場合、当社はお客様に関する情報を開示することがあります。
• 組織再編、合併、または売却の場合、当社は収集した個人情報を該当する後継の第三者に譲渡することがあります。

個人情報の保護

当社は、お客様の個人情報を紛失、盗難、悪用、および不正アクセス、開示、改ざん、破壊から保護するために、管理的、技術的、物理的な予防策を講じます。

会社レベルでのプライバシーの尊重

お客様の個人情報の安全を確保するために、当社はプライバシーとセキュリティの基準を従業員に伝達し、プライバシー慣行を厳格に実施します。

ご存知のとおり、式にべき乗を掛ける場合、それらの指数は常に加算されます (a b *a c = a b+c)。 この数学法則はアルキメデスによって導出され、その後 8 世紀に数学者ヴィラセンが整数の指数の表を作成しました。 対数のさらなる発見に貢献したのは彼らでした。 この関数の使用例は、面倒な乗算を単純な加算によって簡素化する必要があるほとんどの場所で見られます。 この記事を 10 分間読んでいただければ、対数とは何か、そして対数をどのように扱うかについて説明します。 シンプルで親しみやすい言語で。

数学における定義

対数は、次の形式の式です。 log a b=c、つまり、負でない数値 (つまり、正の数値) "b" の底 "a" に対する対数は、累乗 "c とみなされます。最終的に値「b」を得るには、底「a」を累乗する必要があります。 例を使用して対数を分析しましょう。log 2 という式があるとします。 8. 答えを見つけるにはどうすればよいですか? それは非常に簡単です。2 から必要な累乗が 8 になるような累乗を見つける必要があります。頭の中でいくつかの計算を行うと、数字 3 が得られます。 それは真実です。2 の 3 乗により、答えは 8 になるからです。

対数の種類

多くの生徒や学生にとって、このトピックは複雑で理解できないように見えますが、実際には対数はそれほど怖いものではありません、主なことはその一般的な意味を理解し、その特性といくつかの規則を覚えておくことです。 対数式には 3 つの異なるタイプがあります。

1. 自然対数 ln a、底はオイラー数 (e = 2.7)。
2. 10 進数の a。底は 10 です。
3. a>1 を底とする任意の数 b の対数。

それらのそれぞれは、対数定理を使用した単純化、縮小、およびその後の単一対数への縮小などの標準的な方法で解決されます。 対数の正しい値を取得するには、対数の特性と、対数を解くときのアクションの順序を覚えておく必要があります。

ルールといくつかの制限事項

数学では、公理として受け入れられるルール制約がいくつかあります。つまり、それらは議論の対象ではなく、真実です。 たとえば、数値をゼロで割ることは不可能であり、負の数の偶根を抽出することも不可能です。 対数にも独自のルールがあり、これに従うと、長くて量の多い対数式でも操作方法を簡単に学ぶことができます。

• 基底「a」は常にゼロより大きく、1 に等しくない必要があります。そうでない場合、「1」と「0」はどの程度であっても常にその値と等しいため、式は意味を失います。
• a > 0、a b >0 の場合、「c」もゼロより大きくなければならないことがわかります。

対数を解くにはどうすればいいですか?

たとえば、方程式 10 x = 100 の答えを見つけるというタスクが与えられます。これは非常に簡単です。100 になる数値 10 を累乗して累乗を選択する必要があります。もちろん、これは 10 2 = です。 100。

次に、この式を対数形式で表してみましょう。 log 10 100 = 2 が得られます。対数を解くとき、すべてのアクションは実質的に収束して、特定の数値を取得するために対数の底を入力する必要がある累乗を求めます。

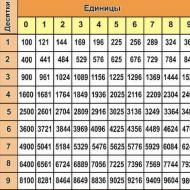
未知の度数の値を正確に判断するには、度数テーブルの操作方法を学ぶ必要があります。 次のようになります。

ご覧のとおり、技術的な知識と九九の知識があれば、一部の指数は直感的に推測できます。 ただし、より大きな値の場合は、電力テーブルが必要になります。 複雑な数学的トピックについてまったく知らない人でも使用できます。 左の列には数値 (基数 a) が含まれており、数値の一番上の行は数値 a を累乗した c の値です。 交点のセルには、答えとなる数値 (a c =b) が含まれています。 たとえば、数字 10 の最初のセルを 2 乗すると、値 100 が得られます。これは 2 つのセルの交点に示されます。 すべてがとてもシンプルで簡単なので、最も真のヒューマニストでも理解できるでしょう。

方程式と不等式

特定の条件下では、指数は対数になることがわかります。 したがって、あらゆる数学的数値表現は対数等式として記述することができます。 たとえば、3 4 =81 は、4 に等しい 81 の 3 を底とする対数として書くことができます (log 3 81 = 4)。 負の累乗の場合もルールは同じです。2 -5 = 1/32 を対数として書くと、log 2 (1/32) = -5 が得られます。 数学の最も魅力的なセクションの 1 つは、「対数」のトピックです。 以下の方程式の性質を調べた直後に、その例と解を見ていきます。 ここで、不等式がどのようなものか、そして不等式と方程式を区別する方法を見てみましょう。

次の式が与えられます: log 2 (x-1) > 3 - 未知の値「x」は対数符号の下にあるため、これは対数不等式です。 また、この式では 2 つの量が比較されます。目的の数値の底 2 に対する対数は、数値 3 よりも大きいです。

対数方程式と不等式の最も重要な違いは、対数を含む方程式 (たとえば、対数 2 x = √9) は答えに 1 つ以上の特定の数値を暗示するのに対し、不等式を解く際には両方の許容範囲が暗示されることです。値とポイントはこの関数を破って決定されます。 結果として、答えは方程式の答えのような単純な個々の数値のセットではなく、連続する一連の数値または数値のセットになります。

対数に関する基本定理

対数の値を求めるという原始的なタスクを解決する場合、その特性がわからない場合があります。 ただし、対数方程式や不等式に関しては、まず対数の基本的な性質をすべて明確に理解し、実際に適用する必要があります。 方程式の例は後で見ていきますが、最初に各プロパティを詳しく見てみましょう。

1. 主な恒等式は次のようになります: a logaB =B。 これは、a が 0 より大きく 1 ではなく、B が 0 より大きい場合にのみ適用されます。
2. 積の対数は、次の式で表すことができます: log d (s 1 * s 2) = log d s 1 + log d s 2。この場合、必須の条件は次のとおりです: d、s 1、および s 2 > 0。 a≠1。 この対数公式を例と解法を使って証明することができます。 log a s 1 = f 1 および log a s 2 = f 2 とすると、a f1 = s 1、a f2 = s 2 となります。 s 1 * s 2 = a f1 *a f2 = a f1+f2 (次のプロパティ) が得られます。度 )、そして定義により、 log a (s 1 * s 2) = f 1 + f 2 = log a s1 + log a s 2、これが証明する必要があるものです。
3. 商の対数は次のようになります: log a (s 1/ s 2) = log a s 1 - log a s 2。
4. 数式の定理は次の形式になります: log a q b n = n/q log a b。

この式を「対数の次数の性質」といいます。 これは通常の学位の特性に似ていますが、すべての数学は自然公準に基づいているため、これは驚くべきことではありません。 証明を見てみましょう。

log a b = t とすると、a t =b になります。 両方の部分を m 乗すると、次のようになります。 a tn = b n ;

しかし、 a tn = (a q) nt/q = b n なので、log a q b n = (n*t)/t となり、log a q b n = n/q log a b となります。 定理は証明されました。

問題と不平等の例

対数に関する最も一般的なタイプの問題は、方程式と不等式の例です。 ほぼすべての問題集に掲載されており、数学の試験でも必須となります。 大学に入学したり、数学の入学試験に合格したりするには、そのような問題を正しく解く方法を知る必要があります。

残念ながら、対数の未知の値を解いて決定するための単一の計画やスキームはありませんが、特定のルールを各数学的不等式または対数方程式に適用できます。 まず第一に、式を簡略化できるか、または一般的な形式に縮小できるかどうかを確認する必要があります。 プロパティを正しく使用すれば、長い対数式を簡略化できます。 早速彼らのことを知りましょう。

対数方程式を解くときは、どのようなタイプの対数があるかを決定する必要があります。式の例には、自然対数または小数の対数が含まれている場合があります。

ln100、ln1026 の例を次に示します。 彼らの解決策は、要するに、底の 10 がそれぞれ 100 と 1026 に等しくなるべき乗を決定する必要があるという事実に帰着します。 自然対数を解くには、対数恒等式またはそのプロパティを適用する必要があります。 さまざまなタイプの対数問題を解く例を見てみましょう。

対数式の使用方法: 例と解決策付き

それでは、対数に関する基本定理の使用例を見てみましょう。

1. 積の対数の特性は、数値 b の大きな値をより単純な因数に分解する必要があるタスクで使用できます。 たとえば、log 2 4 + log 2 128 = log 2 (4*128) = log 2 512。答えは 9 です。
2. log 4 8 = log 2 2 2 3 = 3/2 log 2 2 = 1.5 - ご覧のとおり、対数累乗の 4 番目のプロパティを使用して、一見複雑で解けない式をなんとか解くことができました。 底を因数分解して、対数の符号から指数値を取り出すだけです。

統一州試験の課題

対数は入学試験でよく出題され、特に統一州試験（学校卒業生全員を対象とした州試験）では対数の問題が多く出題されます。 通常、これらのタスクはパート A (試験の最も簡単なテスト部分) だけでなく、パート C (最も複雑で量の多いタスク) にも存在します。 試験では、「自然対数」というトピックについての正確かつ完璧な知識が必要です。

問題の例と解決策は、統一州試験の公式バージョンから引用されています。 このようなタスクがどのように解決されるかを見てみましょう。

log 2 (2x-1) = 4 と仮定します。 解決策:
式を少し単純化して書き直してみましょう。 log 2 (2x-1) = 2 2、対数の定義により、2x-1 = 2 4 となるため、2x = 17 となります。 x = 8.5。

• 解決策が煩雑で混乱しないように、すべての対数を同じ底に換算することが最善です。
• 対数記号の下の式はすべて正として示されるため、対数記号の下にある式の底となる指数を乗数として取り出すとき、対数記号の下に残る式は正でなければなりません。

\(a^(b)=c\) \(\Leftrightarrow\) \(\log_(a)(c)=b\)

もっと簡単に説明しましょう。 たとえば、\(\log_(2)(8)\) は、\(8\) を得るために \(2\) を累乗する必要がある乗数に等しくなります。 このことから、\(\log_(2)(8)=3\) であることがわかります。

引数と対数の底

対数には次のような「構造」があります。

対数の引数は通常、そのレベルで記述され、底は対数の符号に近い添字で記述されます。 そして、このエントリは次のようになります: 「25 を底とする 5 の対数」。

対数を計算するにはどうすればよいですか?

対数を計算するには、引数を得るために底を何乗すべきか?という質問に答える必要があります。

例えば、対数を計算します: a) \(\log_(4)(16)\) b) \(\log_(3)\)\(\frac(1)(3)\) c) \(\log_(\ sqrt (5))(1)\) d) \(\log_(\sqrt(7))(\sqrt(7))\) e) \(\log_(3)(\sqrt(3))\)

a) \(16\) を得るには \(4\) を何乗する必要がありますか? 明らかに2番目です。 それが理由です：

\(\log_(4)(16)=2\)

\(\log_(3)\)\(\frac(1)(3)\) \(=-1\)

c) \(1\) を得るには \(\sqrt(5)\) を何乗する必要がありますか? ナンバーワンを作る力とは何でしょうか？ もちろんゼロですよ！

\(\log_(\sqrt(5))(1)=0\)

d) \(\sqrt(7)\) を得るには \(\sqrt(7)\) を何乗する必要がありますか? まず、数値の 1 乗はそれ自体に等しい。

\(\log_(\sqrt(7))(\sqrt(7))=1\)

e) \(\sqrt(3)\) を得るには \(3\) を何乗する必要がありますか? これは分数べき乗であることがわかります。つまり、平方根は \(\frac(1)(2)\) のべき乗です。

\(\log_(3)(\sqrt(3))=\)\(\frac(1)(2)\)

例 : 対数 \(\log_(4\sqrt(2))(8)\) を計算します

解決 :

答え : \(\log_(4\sqrt(2))(8)=1,2\)

対数はなぜ発明されたのでしょうか?

これを理解するために、方程式 \(3^(x)=9\) を解いてみましょう。 \(x\) を一致させるだけで等価性が機能します。 もちろん \(x=2\) です。

ここで方程式を解きます: \(3^(x)=8\)。x は何に等しいでしょうか? それがポイントです。

最も賢い人は、「X は 2 より少し小さいです」と言うでしょう。 この数字は正確にどのように書くのでしょうか? この質問に答えるために、対数が発明されました。 彼のおかげで、ここでの答えは \(x=\log_(3)(8)\) と書くことができます。

\(\log_(3)(8)\) ということを強調したいのですが、次のようになります。 対数は単なる数値です。 はい、珍しいように見えますが、短いです。 これを 10 進数として書きたい場合は、次のようになります: \(1.892789260714....\)

例 : 方程式 \(4^(5x-4)=10\) を解きます。

解決 :

答え : \(\frac(\log_(4)(10)+4)(5)\)

10 進数と自然対数

対数の定義で述べたように、その底は \((a>0, a\neq1)\) を除く任意の正の数になります。 そして、考えられるすべての基数の中で、非常に頻繁に出現する基数が 2 つあり、それらを使用した対数に対して特別な短い表記法が発明されました。

自然対数: オイラー数 \(e\) (約 \(2.7182818…\) に等しい) を底とする対数。対数は \(\ln(a)\) と書きます。

あれは、 \(\ln(a)\) は \(\log_(e)(a)\) と同じです

10 進対数: 底が 10 の対数は \(\lg(a)\) と書きます。

あれは、 \(\lg(a)\) は \(\log_(10)(a)\) と同じです, ここで \(a\) は数値です。

基本対数恒等式

対数には多くの性質があります。 そのうちの 1 つは「基本対数恒等式」と呼ばれるもので、次のようになります。

このプロパティは定義から直接続きます。 この公式がどのようにして生まれたのかを正確に見てみましょう。

対数の定義の短い表記法を思い出してみましょう。

\(a^(b)=c\) の場合、\(\log_(a)(c)=b\)

つまり、\(b\) は \(\log_(a)(c)\) と同じです。 そうすれば、式 \(a^(b)=c\) で \(b\) の代わりに \(\log_(a)(c)\) と書くことができます。 \(a^(\log_(a)(c))=c\) - 主要な対数恒等式であることが判明しました。

対数の他のプロパティも見つけることができます。 彼らの助けを借りて、直接計算するのが難しい対数を使用した式の値を単純化して計算することができます。

例 : 式 \(36^(\log_(6)(5))\) の値を見つけます。

解決 :

答え : \(25\)

数値を対数として書くにはどうすればよいですか?

上で述べたように、対数は単なる数値です。 逆もまた真で、任意の数値を対数として書くことができます。 たとえば、\(\log_(2)(4)\) は 2 に等しいことがわかります。 次に、2 の代わりに \(\log_(2)(4)\) と書くことができます。

ただし、 \(\log_(3)(9)\) は \(2\) とも等しいため、 \(2=\log_(3)(9)\) と書くこともできます。 \(\log_(5)(25)\) や \(\log_(9)(81)\) などでも同様です。 つまり、判明したのは、

\(2=\log_(2)(4)=\log_(3)(9)=\log_(4)(16)=\log_(5)(25)=\log_(6)(36)=\ log_(7)(49)...\)

したがって、必要に応じて、どこにでも (方程式、式、不等式であっても) 任意の底を持つ対数として 2 を書くことができます。単に引数として底の 2 乗を書くだけです。

トリプルの場合も同様です。\(\log_(2)(8)\)、\(\log_(3)(27)\)、または \(\log_(4)( 64) \)... ここで立方体の基数を引数として書きます。

\(3=\log_(2)(8)=\log_(3)(27)=\log_(4)(64)=\log_(5)(125)=\log_(6)(216)=\ log_(7)(343)...\)

そして4つでは:

\(4=\log_(2)(16)=\log_(3)(81)=\log_(4)(256)=\log_(5)(625)=\log_(6)(1296)=\ log_(7)(2401)...\)

そしてマイナス 1 を付けると次のようになります。

\(-1=\) \(\log_(2)\)\(\frac(1)(2)\) \(=\) \(\log_(3)\)\(\frac(1)( 3)\) \(=\) \(\log_(4)\)\(\frac(1)(4)\) \(=\) \(\log_(5)\)\(\frac(1) )(5)\) \(=\) \(\log_(6)\)\(\frac(1)(6)\) \(=\) \(\log_(7)\)\(\frac (1)(7)\) \(...\)

そして 3 分の 1 では、次のようになります。

\(\frac(1)(3)\) \(=\log_(2)(\sqrt(2))=\log_(3)(\sqrt(3))=\log_(4)(\sqrt( 4))=\log_(5)(\sqrt(5))=\log_(6)(\sqrt(6))=\log_(7)(\sqrt(7))...\)

任意の数値 \(a\) は、底 \(b\) の対数として表すことができます: \(a=\log_(b)(b^(a))\)

例 : 式の意味を調べます \(\frac(\log_(2)(14))(1+\log_(2)(7))\)

解決 :

答え : \(1\)

対数与えられた数の指数は、別の数を累乗する必要がある指数と呼ばれます。 基礎この数値を取得するには対数を使用します。 たとえば、100 の底 10 の対数は 2 です。つまり、100 を得るには 10 を 2 乗する必要があります (10 2 = 100)。 もし n– 指定された数値、 b– ベースと 私– 対数、すると b l = n。 番号 n底の真数とも呼ばれます b数字 私。 たとえば、底 10 に対する 2 の真数は 100 に等しくなります。これは、関係ログの形式で書くことができます。 b n = 私そして真対数 ｂｌ = n.

対数の基本的な性質:

1 以外の正の数は対数の底として機能しますが、残念なことに、 bそして nは有理数ですが、まれにそのような有理数が存在します 私、 何 b l = n。 ただし、無理数を定義することは可能です 私たとえば、10 のようになります。 私= 2; これは無理数です 私有理数によって必要な精度で近似できます。 与えられた例では、 私は約 0.3010 に等しく、2 の底 10 の対数のこの近似は、10 進対数の 4 桁の表で見つけることができます。 底 10 の対数 (または底 10 の対数) は計算でよく使用されるため、以下のように呼ばれます。 普通対数であり、対数の底の明示的な指示を省略して、log2 = 0.3010 または log2 = 0.3010 として記述されます。 底の対数 e、約 2.71828 に等しい超越数は、と呼ばれます。 自然対数。 それらは主に数学的分析とそのさまざまな科学への応用に関する作品に見られます。 自然対数も、底を明示的に示さずに、特殊な表記 ln を使用して記述されます。たとえば、ln2 = 0.6931 です。 e 0,6931 = 2.

常用対数の表を使用します。

数値の正対数は、特定の数値を得るために 10 を累乗する必要がある指数です。 10 0 = 1、10 1 = 10、および 10 2 = 100 であるため、log1 = 0、log10 = 1、log100 = 2 などがすぐにわかります。 整数累乗 10 を増加させます。同様に、10 –1 = 0.1、10 –2 = 0.01 となるため、log0.1 = –1、log0.01 = –2 などとなります。 すべての負の整数乗の場合は 10。残りの数値の通常の対数は、最も近い 10 の整数乗の対数で囲まれます。 log2 は 0 と 1 の間、log20 は 1 と 2 の間、log0.2 は -1 と 0 の間でなければなりません。したがって、対数は 0 と 1 で囲まれた 2 つの部分、整数と小数で構成されます。という整数部分 特性対数であり、数値自体によって決定され、小数部分はと呼ばれます 仮数表から見つけることができます。 また、log20 = log(2̑10) = log2 + log10 = (log2) + 1 です。2 の対数は 0.3010 なので、log20 = 0.3010 + 1 = 1.3010 となります。 同様に、log0.2 = log(2®10) = log2 – log10 = (log2) – 1 = 0.3010 – 1。減算すると、log0.2 = – 0.6990 が得られます。 ただし、log0.2 を 0.3010 – 1 または 9.3010 – 10 として表す方が便利です。 一般的な規則も定式化できます。つまり、10 の累乗を乗算して指定された数値から得られるすべての数値は、指定された数値の仮数に等しい同一の仮数を持ちます。 他のすべての数値の仮数は表に示されている仮数から取得できるため、ほとんどの表には 1 から 10 の範囲の数値の仮数が表示されます。

ほとんどの表では、小数点以下 4 桁または 5 桁の対数が表示されますが、7 桁の表や小数点以下の桁数がさらに多い表もあります。 このようなテーブルの使用方法を学ぶ最も簡単な方法は、例を使用することです。 log3.59 を見つけるには、まず、数値 3.59 が 10 0 と 10 1 の間にあるため、その特性は 0 であることに注意します。テーブル内で数値 35 (左側) を見つけ、行に沿って先頭に数字 9 がある列。 この列と行 35 の交点は 5551 であるため、log3.59 = 0.5551 となります。 有効数字 4 桁の数値の仮数を見つけるには、内挿を使用する必要があります。 一部の表では、表の各ページの右側の最後の 9 列に示されている比率によって補間が容易になります。 ここで、log736.4 を見つけてみましょう。 数値 736.4 は 10 2 と 10 3 の間にあるため、その対数の特性は 2 です。表では、73 という行の左側と 6 列目が見つかります。この行とこの列の交点には、直線部分の中で列 4 が見つかります。行 73 と列 4 の交点に数字 2 があります。8669 に 2 を加算すると、仮数が得られます。仮数は 8671 に等しくなります。したがって、log736.4 = 2.8671。

自然対数。

自然対数のテーブルとプロパティは、通常の対数のテーブルとプロパティに似ています。 両者の主な違いは、自然対数の整数部分は小数点の位置を決定する際に重要ではないため、仮数と特性の差は特別な役割を果たさないことです。 数値の自然対数 5.432。 54.32 と 543.2 はそれぞれ 1.6923 に等しくなります。 3.9949 と 6.2975。 これらの対数間の関係は、それらの差を考慮すると明らかになります。log543.2 – log54.32 = 6.2975 – 3.9949 = 2.3026; 最後の数値は数値 10 の自然対数にすぎません (ln10 のように記述されます)。 log543.2 – log5.432 = 4.6052; 最後の数字は 2ln10 です。 ただし、543.2 = 10 54.32 = 10 2 5.432 となります。 したがって、与えられた数の自然対数により、 ある数値の積に等しい数値の自然対数を見つけることができます あるいかなる学位でも n ln の場合は数字 10 ある ln10 を加算して乗算 n、つまり ln( あるґ10n) = ログ ある + n ln10 = ln ある + 2,3026n。 たとえば、ln0.005432 = ln(5.432̑10 –3) = ln5.432 – 3ln10 = 1.6923 – (3̑2.3026) = – 5.2155。 したがって、常対数の表と同様に、自然対数の表には、通常、1 から 10 までの数値の対数のみが含まれます。自然対数系では、真数について話すこともできますが、より多くの場合、指数関数または指数について話します。 もし バツ= ログ y、 それ y = 元、 そして yの指数と呼ばれる バツ(活版印刷の便宜上、彼らはしばしば次のように書きます) y= 経験値 バツ）。 指数は数値の真数の役割を果たします。 バツ.

10 進対数と自然対数のテーブルを使用すると、10 以外の底の対数のテーブルを作成できます。 e。 ログの場合 b a = バツ、 それ bx = あるしたがってログに記録します cbx= ログ c aまたは バツログ c b= ログ c a、 または バツ= ログ c a/ログ c b= ログ b a。 したがって、底対数表からこの逆数式を使用すると、 c他の底で対数の表を作成できます b。 乗数 1/log c b呼ばれた 移行モジュール基地から c基地へ b。 たとえば、反転公式を使用したり、ある対数系から別の対数系に移行したり、常用対数の表から自然対数を見つけたり、逆の移行を行ったりすることを妨げるものはありません。 たとえば、log105.432 = ログ e 5.432/ログ e 10 = 1.6923/2.3026 = 1.6923̑0.4343 = 0.7350。 常対数を得るために、指定された数の自然対数に乗算する必要がある数値 0.4343 は、常対数系への遷移の係数です。

特別なテーブル。

対数はもともと、その特性を使用して対数を計算するために発明されました。 腹筋= ログ ある+ログ bそしてログを記録します ある/b= ログ ある– ログ b、積を和に、商を差に変えます。 つまり、ログの場合、 あるそしてログを記録します bがわかっている場合は、加算と減算を使用して、積と商の対数を簡単に求めることができます。 しかし、天文学では、対数の値が与えられることがよくあります。 あるそしてログを記録します bログを見つける必要があります( ある + b) またはログ( ある – b）。 もちろん、最初に対数表から見つけることもできます。 あるそして b、次に、指定された加算または減算を実行し、再度テーブルを参照して必要な対数を見つけます。ただし、そのような手順ではテーブルを 3 回参照する必要があります。 Z. Leonelli は 1802 年にいわゆる表を出版しました。 ガウス対数– 和と差を加算するための対数 – これにより、テーブルへのアクセスを 1 回に制限することが可能になりました。

1624 年、I. ケプラーは比例対数の表を提案しました。 数値の対数 ある/バツ、 どこ ある– 何らかの正の定数値。 これらのテーブルは主に天文学者や航海士によって使用されます。

比例対数 ある= 1 が呼び出されます 対数積や商を扱う必要がある場合の計算に使用されます。 数値の対数 n逆数の対数に等しい。 それらの。 コログ n= log1/ n= – ログ n。 log2 = 0.3010 の場合、colog2 = – 0.3010 = 0.6990 – 1 となります。 対数を使用する利点は、次のような式の対数値を計算する場合にあることです。 pq/r正の小数の対数の 3 倍の和 p+ログ q+コログ r混合和と差のログよりも見つけやすい p+ログ q– ログ r.

話。

対数系の基礎となる原理は非常に古くから知られており、古代バビロニア数学 (紀元前 2000 年頃) にまで遡ることができます。 当時、複利の計算には、整数の正の整乗のテーブル値間の補間が使用されていました。 ずっと後になって、アルキメデス (紀元前 287 ～ 212 年) は 108 乗を使って、当時知られていた宇宙を完全に埋めるのに必要な砂粒の数の上限を見つけました。 アルキメデスは、対数の有効性の基礎となる指数の性質、つまりべき乗の積は指数の合計に対応することに注目しました。 中世の終わりから近代の初めにかけて、数学者は等比数列と等差数列の関係にますます注目し始めました。 M. シュティーフェルのエッセイ 整数演算(1544) は、数 2 の正と負の累乗の表を示しました。

シュティーフェルは、最初の行 (指数行) の 2 つの数値の合計が、一番下の行 (指数行) の対応する 2 つの数値の積に対応する 2 の指数に等しいことに気づきました。 この表に関連して、シュティーフェルは、指数演算の 4 つの現代規則または対数演算の 4 つの規則に相当する 4 つの規則を定式化しました。つまり、上の行の合計は下の行の積に対応します。 上の行の減算は下の行の除算に対応します。 上の行の乗算は下の行のべき乗に対応します。 上の行の分割は下の行のルート化に対応します。

どうやら、シュティーフェルの規則に似た規則が、J. ネイパーの作品に最初の対数系を正式に導入するきっかけとなったようです。 驚くべき対数表の説明しかし、彼の著作が出版される10年以上前に、ネイピアはデンマークから、ティコ・ブラーエ天文台で彼の助手たちが、積を合計に換算することが可能です。 ネイピアが受け取ったメッセージで説明されている方法は、次のような三角関数の公式の使用に基づいていました。

したがって、ネイパーの表は主に三角関数の対数で構成されていました。 底の概念はネイピアによって提案された定義には明示的に含まれていませんでしたが、彼の体系における対数系の底に相当する役割は、1/ にほぼ等しい数値 (1 – 10 –7)̑10 7 によって演じられました。 e.

ナパーとは独立して、そしてほぼ同時に、タイプが非常に似た対数系がプラハの J. ビュルギによって発明され、1620 年に出版されました。 算術および等比数列表。 これらは底 (1 + 10 –4) 10 4 の真数の表であり、数値のかなり良い近似値です。 e.

Naper システムでは、数値 10 7 の対数がゼロとみなされ、数値が減少すると対数が増加します。 G. ブリッグス (1561–1631) がネーピアを訪れたとき、両者は 10 という数字を底として使用し、1 の対数をゼロとみなす方が便利であることに同意しました。 次に、数値が増加するにつれて、対数も増加します。 このようにして、現代の 10 進対数体系が得られ、その表はブリッグスが著書の中で発表しました。 対数演算（1620年）。 底の対数 e、正確には Naper によって紹介されたものではありませんが、Naper's と呼ばれることがよくあります。 「特性」と「仮数」という用語はブリッグスによって提案されました。

最初の対数は、歴史的な理由から、数値 1/ の近似値を使用していました。 eそして e。 少し後、自然対数の考え方は双曲線の下の領域の研究と関連付けられ始めました。 xy= 1 (図 1)。 17世紀に この曲線で囲まれた領域、軸が バツと縦座標 バツ= 1 および バツ = ある(図 1 では、この領域は太くてまばらな点で覆われています) ある指数関数的に増加します。 指数と対数の演算ルールで生じるのは、まさにこの依存性です。 これにより、ネーペリアン対数を「双曲線対数」と呼ぶようになりました。

対数関数。

対数が計算の手段としてのみ考慮されていた時代もありましたが、18 世紀には主にオイラーの研究のおかげで、対数関数の概念が形成されました。 このような関数のグラフ y= ログ バツ、縦軸は等差数列で増加し、横軸は等比数列で増加しますが、図に示されています。 2、 あ。 逆関数または指数関数のグラフ y = e x、縦軸が等差数列で増加し、横軸が等差数列で増加することをそれぞれ図に示します。 2、 b。 (曲線 y= ログ バツそして y = 10バツ曲線に似た形状 y= ログ バツそして y = 元.) 対数関数の別の定義も提案されています。

kpi ; 同様に、数値 -1 の自然対数は、次の形式の複素数です (2 k + 1)円周率、 どこ k– 整数。 同様の記述は、一般対数または他の対数系にも当てはまります。 さらに、対数の定義はオイラーの恒等式を使用して一般化し、複素数の複素対数を含めることができます。

対数関数の別の定義は、関数分析によって提供されます。 もし f(バツ) – 実数の連続関数 バツ、次の 3 つのプロパティがあります。 f (1) = 0, f (b) = 1, f (紫外線) = f (あなた) + f (v）、 それ f(バツ) は数値の対数として定義されます。 バツに基づく b。 この定義には、この記事の冒頭で示した定義よりも多くの利点があります。

アプリケーション。

対数はもともと計算を簡素化するためにのみ使用されていましたが、この応用は今でも最も重要なものの 1 つです。 積、商、累乗、根の計算は、公開されている対数表が広く利用できるだけでなく、いわゆる対数表を使用することによっても容易になります。 計算尺 - 動作原理が対数の特性に基づいている計算ツール。 定規には対数スケールが装備されています。 数値 1 から任意の数値までの距離 バツ log と等しくなるように選択される バツ; あるスケールを別のスケールに対して移動することにより、対数の和や差をプロットすることができ、対応する数値の積や商をスケールから直接読み取ることが可能になります。 数値を対数形式で表すことの利点を活用することもできます。 グラフを描くための対数紙（両座標軸に対数目盛りが印刷された紙）。 関数が次の形式のべき乗則を満たす場合、 y = kxnの場合、その対数グラフは直線のように見えます。 ログ y= ログ k + nログ バツ– 対数に関して線形の方程式 yそしてログを記録します バツ。 逆に、ある関数依存性の対数グラフが直線のように見える場合、その依存性はべき乗依存性です。 指数関数を識別する必要がある場合は、半対数紙 (Y 軸が対数スケールで、X 軸が均一のスケールを持つ) が便利です。 次の形式の方程式 y = kb rx人口、放射性物質の量、銀行残高などの量が、現在利用可能な人口、放射性物質、またはお金の量に比例した割合で減少または増加するたびに発生します。 このような依存関係を片対数紙にプロットすると、グラフは直線のように見えます。

対数関数は、さまざまな自然の形態に関連して発生します。 ヒマワリの花序の花は対数螺旋状に配置され、軟体動物の殻はねじれています オウムガイ、山羊の角とオウムのくちばし。 これらの自然な形状はすべて、対数螺旋として知られる曲線の例として機能します。極座標系では、その方程式は次のとおりです。 r = ae bq、またはln r= ログ ある + バーベキュー。 このような曲線は移動点によって表され、その極からの距離は等比数列で増加し、その動径ベクトルによって表される角度は等差数列で増加します。 このような曲線、したがって対数関数の遍在性は、それが偏心カムの輪郭や光に向かって飛んでいく昆虫の軌跡など、遠く離れたまったく異なる領域で発生するという事実によってよく示されています。