X saknes grafiks. X sakne no x ir vienāda. Piemērs. Sakņu sakne

Ir dotas jaudas funkcijas pamatīpašības, ieskaitot formulas un sakņu īpašības. Tiek parādīts jaudas funkcijas atvasinājums, integrālis, pakāpju rindas paplašinājums un komplekso skaitļu attēlojums.

Saturs

Jaudas funkcijai y = x p ar eksponentu p ir šādas īpašības:
(1.1) noteikti un nepārtraukti filmēšanas laukumā
plkst ,
pie ;
(1.2) ir daudz nozīmju
plkst ,
pie ;
(1.3) stingri palielinās ar ,
stingri samazinās kā ;
(1.4) pie ;
pie ;
(1.5) ;
(1.5*) ;
(1.6) ;
(1.7) ;
(1.7*) ;
(1.8) ;
(1.9) .

Rekvizītu apliecinājums ir sniegts lapā “Jaudas funkcija (nepārtrauktības un īpašību pierādījums)”

Saknes - definīcija, formulas, īpašības

Skaitļa x ar pakāpju n sakne ir skaitlis, kuru, palielinot līdz pakāpei n, iegūst x:
.
Šeit n = 2, 3, 4, ... - naturāls skaitlis, kas lielāks par vienu.

Varat arī teikt, ka skaitļa x sakne ar pakāpi n ir vienādojuma sakne (t.i., atrisinājums).
.
Ņemiet vērā, ka funkcija ir apgriezta funkcijai.

No x kvadrātsakne ir 2 sakne: .
X kuba sakne ir 3. sakne: .

Vienmērīgs grāds

Pāra pakāpēm n = 2 m, sakne ir definēta x ≥ 0 . Bieži lietotā formula ir derīga gan pozitīvam, gan negatīvam x:
.
Kvadrātsaknei:
.

Šeit svarīga ir darbību veikšanas secība - tas ir, vispirms tiek izpildīts kvadrāts, kā rezultātā tiek iegūts nenegatīvs skaitlis, un tad no tā tiek ņemta sakne (kvadrātsakni var ņemt no nenegatīva skaitļa ). Ja mēs mainītu secību: , tad negatīvam x sakne būtu nedefinēta, un līdz ar to visa izteiksme būtu nedefinēta.

Nepāra pakāpe

Nepāra pakāpēm sakne ir definēta visiem x:
;
.

Sakņu īpašības un formulas

X sakne ir jaudas funkcija:
.
Kad x ≥ 0 tiek piemērotas šādas formulas:
;
;
, ;
.

Šīs formulas var izmantot arī mainīgo lielumu negatīvajām vērtībām. Jums tikai jāpārliecinās, ka vienmērīgu spēku radikālā izpausme nav negatīva.

Privātās vērtības

0 sakne ir 0: .
1. sakne ir vienāda ar 1: .
Kvadrātsakne no 0 ir 0: .
Kvadrātsakne no 1 ir 1: .

Piemērs. Sakņu sakne

Apskatīsim sakņu kvadrātsaknes piemēru:
.
Pārveidosim iekšējo kvadrātsakni, izmantojot iepriekš minētās formulas:
.
Tagad pārveidosim sākotnējo sakni:
.
Tātad,
.

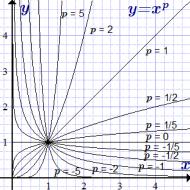
y = x p dažādām eksponenta p vērtībām.

Šeit ir funkcijas grafiki argumenta x nenegatīvajām vērtībām. Jaudas funkcijas grafiki, kas definēti x negatīvajām vērtībām, ir sniegti lapā "Jaudas funkcija, tās īpašības un grafiki"

Apgrieztā funkcija

Jaudas funkcijas apgrieztā vērtība ar eksponentu p ir pakāpes funkcija ar eksponentu 1/p.

Ja tad.

Jaudas funkcijas atvasinājums

N-tās kārtas atvasinājums:
;

Formulu atvasināšana >>>

Jaudas funkcijas integrāls

P ≠ - 1 ;
.

Jaudas sērijas paplašināšana

plkst - 1 < x < 1 notiek šāda sadalīšanās:

Izteiksmes, izmantojot kompleksos skaitļus

Apsveriet kompleksā mainīgā z funkciju:
f (z) = z t.
Izteiksim komplekso mainīgo z ar moduli r un argumentu φ (r = |z|):
z = r e i φ .
Mēs attēlojam komplekso skaitli t reālu un iedomātu daļu veidā:
t = p + i q .
Mums ir:

Tālāk mēs ņemam vērā, ka arguments φ nav unikāli definēts:
,

Apskatīsim gadījumu, kad q = 0 , tas ir, eksponents ir reāls skaitlis, t = p. Tad
.

Ja p ir vesels skaitlis, tad kp ir vesels skaitlis. Pēc tam trigonometrisko funkciju periodiskuma dēļ:
.
Tas ir, eksponenciālajai funkcijai ar veselu eksponentu konkrētam z ir tikai viena vērtība, un tāpēc tā ir nepārprotama.

Ja p ir iracionāls, tad reizinājumi kp jebkuram k nerada veselu skaitli. Tā kā k iet cauri bezgalīgai vērtību sērijai k = 0, 1, 2, 3, ..., tad funkcijai z p ir bezgalīgi daudz vērtību. Ikreiz, kad arguments z tiek palielināts 2π(viens pagrieziens), mēs pārejam uz jaunu funkcijas atzaru.

Ja p ir racionāls, tad to var attēlot šādi:
, Kur m, n- veseli skaitļi, kas nesatur kopīgus dalītājus. Tad
.
Pirmās n vērtības, kur k = k 0 = 0, 1, 2, ... n-1, dodiet n dažādas kp vērtības:
.
Tomēr nākamās vērtības dod vērtības, kas atšķiras no iepriekšējām par veselu skaitli. Piemēram, kad k = k 0+n mums ir:
.
Trigonometriskās funkcijas, kuru argumenti atšķiras ar daudzkārtņiem 2π, ir vienādas vērtības. Tāpēc, vēl vairāk palielinot k, mēs iegūstam tādas pašas z p vērtības kā k = k 0 = 0, 1, 2, ... n-1.

Tādējādi eksponenciāla funkcija ar racionālu eksponentu ir daudzvērtīga, un tai ir n vērtības (zari). Ikreiz, kad arguments z tiek palielināts 2π(viens pagrieziens), mēs pārejam uz jaunu funkcijas atzaru. Pēc n šādiem apgriezieniem mēs atgriežamies pie pirmā atzara, no kuras sākās atpakaļskaitīšana.

Jo īpaši n pakāpes saknei ir n vērtības. Kā piemēru ņemiet vērā reāla pozitīva skaitļa n-to sakni z = x. Šajā gadījumā φ 0 = 0 , z = r = |z| = x, .
.
Tātad kvadrātsaknei n = 2 ,
.
Pat k, (- 1 ) k = 1. nepāra k, (- 1 ) k = - 1.
Tas ir, kvadrātsaknei ir divas nozīmes: + un -.

Atsauces:
I.N. Bronšteins, K.A. Semendjajevs, Matemātikas rokasgrāmata inženieriem un koledžas studentiem, “Lan”, 2009.

Skatīt arī:

Kvadrātsakne kā elementāra funkcija.

Kvadrātsakne ir elementāra funkcija un īpašs jaudas funkcijas gadījums . Aritmētiskā kvadrātsakne ir gluda pie , un pie nulles tā ir taisna nepārtraukta, bet nav diferencējama.

Kā funkcija kompleksa mainīgā sakne ir divu vērtību funkcija, kuras lapas saplūst pie nulles.

Kvadrātsaknes funkcijas grafiks.

1. Datu tabulas aizpildīšana:

X
plkst

2. Saņemtos punktus uzzīmējam koordinātu plaknē.

3. Savienojiet šos punktus un iegūstiet kvadrātsaknes funkcijas grafiku:

Kvadrātsaknes funkcijas grafika pārveidošana.

Noskaidrosim, kādas funkciju transformācijas ir jāveic, lai izveidotu funkciju grafikus. Definēsim transformāciju veidus.

	Konversijas veids	Pārvēršana
		Funkcijas pārsūtīšana pa asi OY par 4 vienībām uz augšu.
	iekšējais	Funkcijas pārsūtīšana pa asi VĒRSIS par 1 vienību pa labi.
	iekšējais	Grafiks tuvojas asij OY 3 reizes un saspiež pa asi Ak!.
		Grafiks attālinās no ass VĒRSIS OY.
	iekšējais	Grafiks attālinās no ass OY 2 reizes un izstiepts pa asi Ak!.

Bieži vien funkciju transformācijas tiek apvienotas.

Piemēram, jums ir jāatzīmē funkcija . Šis ir kvadrātsaknes grafiks, kas jāpārvieto par vienu vienību uz leju pa asi OY un vienu vienību pa labi pa asi Ak! un tajā pašā laikā izstiepjot to 3 reizes pa asi OY.

Gadās, ka tieši pirms funkcijas grafika konstruēšanas ir nepieciešamas iepriekšējas identitātes transformācijas vai funkciju vienkāršojumi.

Vai meklējāt x sakni no x vienādības? . Detalizēts risinājums ar aprakstu un paskaidrojumiem palīdzēs tikt galā ar pat vissarežģītākajām problēmām, un x ir y sakne, nav izņēmums. Palīdzēsim sagatavoties mājas darbiem, ieskaitēm, olimpiādēm, kā arī iestājai augstskolā. Un neatkarīgi no piemēra, neatkarīgi no ievadītā matemātikas vaicājuma, mums jau ir risinājums. Piemēram, “x ir vienāds ar x sakne”.

Mūsu dzīvē ir plaši izplatīta dažādu matemātisko uzdevumu, kalkulatoru, vienādojumu un funkciju izmantošana. Tos izmanto daudzos aprēķinos, konstrukciju būvniecībā un pat sportā. Cilvēks matemātiku ir izmantojis kopš seniem laikiem un kopš tā laika to lietojums ir tikai palielinājies. Tomēr tagad zinātne nestāv uz vietas un mēs varam baudīt tās darbības augļus, piemēram, tiešsaistes kalkulatoru, kas var atrisināt tādas problēmas kā x sakne no x ir vienāda, x sakne no y, sakne no x, sakne no x ir vienāda ar x sakne no x ir vienāda ar x, sakne no x ir vienāda ar x, funkcija y ir sakne no mīnus x, funkcija y mīnus sakne no x, x ir sakne no y, x ir sakne no x ir vienāda ar. Šajā lapā jūs atradīsiet kalkulatoru, kas palīdzēs atrisināt jebkuru jautājumu, ieskaitot x sakni no x vienāds. (piemēram, x sakne).

Kur jūs varat atrisināt jebkuru uzdevumu matemātikā, kā arī x sakne no x vienāda tiešsaistē?

Jūs varat atrisināt problēmu x sakne no x vienāds mūsu vietnē. Bezmaksas tiešsaistes risinātājs ļaus jums dažu sekunžu laikā atrisināt jebkuras sarežģītības tiešsaistes problēmu. Viss, kas jums jādara, ir vienkārši ievadīt savus datus risinātājā. Varat arī noskatīties video instrukcijas un uzzināt, kā pareizi ievadīt savu uzdevumu mūsu vietnē. Un, ja jums joprojām ir jautājumi, varat tos uzdot tērzēšanā kalkulatora lapas apakšējā kreisajā stūrī.

Nodarbība un prezentācija par tēmu: "Kvadrātsaknes funkcijas grafiks. Grafika definīcijas un uzbūves joma"

Papildu materiāli
Cienījamie lietotāji, neaizmirstiet atstāt savus komentārus, atsauksmes, vēlmes. Visi materiāli ir pārbaudīti ar pretvīrusu programmu.

Mācību līdzekļi un simulatori Interneta veikalā Integral 8. klasei
Mordkoviča A.G. elektroniskā mācību grāmata mācību grāmatai.
Elektroniskā algebras darba burtnīca 8. klasei

Kvadrātsaknes funkcijas grafiks

Puiši, mēs jau esam tikušies ar funkciju grafiku veidošanu un vairāk nekā vienu reizi. Mēs izveidojām daudzas lineāras funkcijas un parabolas. Kopumā jebkuru funkciju ir ērti rakstīt kā $y=f(x)$. Šis ir vienādojums ar diviem mainīgajiem - katrai x vērtībai mēs iegūstam y. Veicot noteiktu darbību f, mēs kartējam visu iespējamo x kopu ar kopu y. Gandrīz jebkuru matemātisko darbību varam uzrakstīt kā funkciju f.

Parasti, attēlojot funkcijas, mēs izmantojam tabulu, kurā ierakstām x un y vērtības. Piemēram, funkcijai $y=5x^2$ ir ērti izmantot šādu tabulu: Atzīmējiet iegūtos punktus Dekarta koordinātu sistēmā un uzmanīgi savienojiet tos ar gludu līkni. Mūsu funkcija nav ierobežota. Tikai ar šiem punktiem mēs varam aizstāt absolūti jebkuru vērtību x no dotā definīcijas domēna, tas ir, tos x, kuriem izteiksmei ir jēga.

Vienā no iepriekšējām nodarbībām mēs apguvām jaunu ekstrakcijas darbību kvadrātsakne. Rodas jautājums: vai, izmantojot šo darbību, mēs varam definēt kādu funkciju un izveidot tās grafiku? Izmantosim funkcijas $y=f(x)$ vispārīgo formu. Atstāsim to vietā y un x, un f vietā ieviesīsim kvadrātsaknes operāciju: $y=\sqrt(x)$.
Zinot matemātisko darbību, varējām definēt funkciju.

Kvadrātsaknes funkcijas grafiks

Grafikosim šo funkciju. Pamatojoties uz kvadrātsaknes definīciju, mēs to varam aprēķināt tikai no nenegatīviem skaitļiem, tas ir, $x≥0$.
Izveidosim tabulu:
Atzīmēsim savus punktus koordinātu plaknē.

Viss, kas mums jādara, ir rūpīgi savienot iegūtos punktus.

Puiši, pievērsiet uzmanību: ja mūsu funkcijas grafiks ir pagriezts uz sāniem, mēs iegūstam parabolas kreiso zaru. Faktiski, ja vērtību tabulas rindas tiek apmainītas (augšējā līnija ar apakšējo), tad mēs iegūstam vērtības tikai parabolai.

Funkcijas $y=\sqrt(x)$ domēns

Izmantojot funkcijas grafiku, ir diezgan viegli aprakstīt īpašības.
1. Definīcijas joma: $$.
b) $$.

Risinājums.
Mēs varam atrisināt mūsu piemēru divos veidos. Katrā vēstulē mēs aprakstīsim dažādas metodes.

A) Atgriezīsimies pie iepriekš konstruētās funkcijas grafika un atzīmēsim vajadzīgos segmenta punktus. Ir skaidri redzams, ka $x=9$ funkcija ir lielāka par visām pārējām vērtībām. Tas nozīmē, ka šajā brīdī tas sasniedz savu lielāko vērtību. Ja $x=4$, funkcijas vērtība ir mazāka par visiem citiem punktiem, kas nozīmē, ka šī ir mazākā vērtība.

$y_(visvairāk)=\sqrt(9)=3$, $y_(visvairāk)=\sqrt(4)=2$.

B) Mēs zinām, ka mūsu funkcija palielinās. Tas nozīmē, ka katra lielāka argumenta vērtība atbilst lielākai funkcijas vērtībai. Augstākās un zemākās vērtības tiek sasniegtas segmenta beigās:

$y_(visvairāk)=\sqrt(11)$, $y_(visvairāk)=\sqrt(2)$.

2. piemērs.
Atrisiniet vienādojumu:

$\sqrt(x)=12-x$.

Risinājums.
Vienkāršākais veids ir izveidot divus funkcijas grafikus un atrast to krustpunktu.
Grafikā skaidri redzams krustojuma punkts ar koordinātām $(9;3)$. Tas nozīmē, ka $x=9$ ir mūsu vienādojuma risinājums.
Atbilde: $x=9$.

Puiši, vai varam būt pārliecināti, ka šim piemēram nav vairāk risinājumu? Viena no funkcijām palielinās, otra samazinās. Kopumā tiem vai nu nav kopīgu punktu, vai arī tie krustojas tikai vienā.

3. piemērs.

Izveidojiet un nolasiet funkcijas grafiku:

$\begin (cases) -x, x 9. \end (cases)$

Mums ir jākonstruē trīs funkcijas daļējie grafiki, katrs savā intervālā.

Aprakstīsim mūsu funkcijas īpašības:
1. Definīcijas domēns: $(-∞;+∞)$.
2. $y=0$ pie $x=0$ un $x=12$; $у>0$ par $хϵ(-∞;12)$; $y 3. Funkcija samazinās uz intervāliem $(-∞;0)U(9;+∞)$. Funkcija pieaug intervālā $(0;9)$.
4. Funkcija ir nepārtraukta visā definīcijas jomā.
5. Nav maksimālās vai minimālās vērtības.
6. Vērtību diapazons: $(-∞;+∞)$.

Problēmas, kas jārisina patstāvīgi

1. Atrodiet segmenta kvadrātsaknes funkcijas lielāko un mazāko vērtību:
a) $$;
b) $$.
2. Atrisiniet vienādojumu: $\sqrt(x)=30-x$.
3. Izveidojiet un nolasiet funkcijas grafiku: $\begin (cases) 2-x, x 4. \end (cases)$
4. Izveidojiet un nolasiet funkcijas grafiku: $y=\sqrt(-x)$.

Facebook

Twitter

Saskarsmē ar

Klasesbiedriem

Google+