x の根のグラフ。 x の x 根は等しい。例。根の根

累乗関数の基本的な特性 (式や根の特性など) が示されています。べき乗関数の導関数、積分、べき級数展開、および複素数表現が表示されます。

コンテンツ

指数 p を持つべき乗関数 y = x p には、次の特性があります。
(1.1) セット上で定義され、継続的である
で、
で ;
(1.2) 多くの意味があります
で、
で ;
(1.3) 厳密に増加すると、
厳密には次のように減少します。
(1.4) で ;
で ;
(1.5) ;
(1.5*) ;
(1.6) ;
(1.7) ;
(1.7*) ;
(1.8) ;
(1.9) .

性質の証明は「べき乗関数（連続性と性質の証明）」のページに記載されています。

ルート - 定義、公式、プロパティ

数値 x の n 乗根は、n 乗すると x となる数値です。
.
ここで n = 2, 3, 4, ... - 1 より大きい自然数。

n 次の数値 x の根が方程式の根 (つまり、解) であるとも言えます。
.
この関数は関数の逆関数であることに注意してください。

x の平方根は 2 の根です: 。
x の立方根は 3 番目の根です: 。

偶数度

偶数乗の場合、n = 2m、ルートは x ≥ に対して定義されます。 0 。よく使用される式は、正の x と負の x の両方に有効です。
.
平方根の場合:
.

ここでは、演算を実行する順序が重要です。つまり、最初に二乗が実行されて非負の数が得られ、次にそこからルートが取得されます (平方根は非負の数から取得できます)。）。順序を変更すると、負の x のルートは未定義になり、式全体が未定義になります。

奇数度

奇数乗の場合、根はすべての x に対して定義されます。
;
.

ルートの性質と公式

x の根はべき乗関数です。
.
x≧の場合 0 次の式が適用されます。
;
;
, ;
.

これらの式は変数の負の値にも適用できます。偶数乗の急進的な表現が否定的ではないことを確認する必要があるだけです。

プライベートな価値観

0 のルートは 0: です。
ルート 1 は 1 に等しい: 。
0 の平方根は 0: です。
1 の平方根は 1: です。

例。根の根

根の平方根の例を見てみましょう。
.
上記の式を使用して内側の平方根を変換しましょう。
.
次に、元のルートを変換しましょう。
.
それで、
.

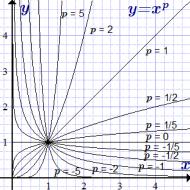
指数 p のさまざまな値の場合は y = x p。

以下は、引数 x の非負の値に対する関数のグラフです。 x の負の値に対して定義されたべき乗関数のグラフは、「べき乗関数、そのプロパティとグラフ」のページに記載されています。

逆関数

指数 p のべき乗関数の逆関数は、指数 1/p のべき乗関数です。

もしそうなら。

べき乗関数の導関数

n次微分:
;

数式の導出 > > >

べき乗関数の積分

P ≠ - 1 ;
.

べき級数展開

で - 1 < x < 1 次の分解が行われます。

複素数を使った式

複素変数 z の関数を考えてみましょう。
f (z) = zt.
複素変数 z を法 r と引数 φ で表現してみましょう (r = |z|)。
z = r e i φ 。
複素数 t を実数部と虚数部の形式で表します。
t = p + i q 。
我々は持っています：

次に、引数 φ が一意に定義されていないことを考慮します。
,

q = の場合を考えてみましょう。 0 つまり、指数は実数 t = p です。それから
.

p が整数の場合、kp は整数です。次に、三角関数の周期性により、次のようになります。
.
つまり、指定された z に対して、整数の指数を持つ指数関数は値を 1 つだけ持つため、明確になります。

p が無理数の場合、任意の k に対する積 kp は整数を生成しません。 k は無限の一連の値を実行するため、 k = 0、1、2、3、...の場合、関数 z p は無限に多くの値を持ちます。引数 z がインクリメントされるたびに 2π(1 ターン)、関数の新しいブランチに移動します。

p が有理数の場合、次のように表すことができます。
、どこメートル、ン- 公約数を含まない整数。それから
.
最初の n 値、k = k 0 = 0、1、2、...n-1、n個の異なるkp値を与える：
.
ただし、後続の値は、前の値とは整数だけ異なる値を与えます。たとえば、k = k の場合、 0+n我々は持っています：
.
引数が次の倍数異なる三角関数 2π、等しい値を持ちます。したがって、kをさらに増やすと、k = kの場合と同じz p の値が得られます。 0 = 0、1、2、...n-1.

したがって、有理指数を持つ指数関数は多値であり、n 個の値 (分岐) を持ちます。引数 z がインクリメントされるたびに 2π(1 ターン)、関数の新しいブランチに移動します。このような n 回転の後、カウントダウンが開始された最初のブランチに戻ります。

特に、次数 n の根には n 個の値があります。例として、正の実数 z = x の n 乗根を考えてみましょう。この場合、φ 0 = 0 、z = r = |z| = x, .
.
したがって、平方根の場合、n = 2 ,
.
偶数 k については、 (-1) k = 1。奇数 k の場合、 (-1) k = -1.
つまり、平方根には + と - の 2 つの意味があります。

参考文献:
で。ブロンスタイン、K.A. Semendyaev、エンジニアと大学生のための数学ハンドブック、「Lan」、2009 年。

以下も参照してください。

初等関数としての平方根。

平方根は初等関数であり、のべき乗関数の特殊なケースです。算術平方根はでは滑らかで、ゼロでは正しく連続ですが微分可能ではありません。

関数としては、複素変数 root は 2 値関数であり、その葉は 0 に収束します。

平方根関数をグラフ化します。

データテーブルに記入します。

バツ
で

2. 受け取った点を座標平面上にプロットします。

3. これらの点を接続し、平方根関数のグラフを取得します。

平方根関数のグラフを変形します。

関数グラフを構築するためにどのような関数変換を行う必要があるかを判断してみましょう。変換の種類を定義しましょう。

	変換タイプ	変換
		軸に沿った関数の転送ああ 4台用上。
	内部	軸に沿った関数の転送牛 1台分右の方へ。
	内部	グラフが軸に近づくああ 3回で軸に沿って圧縮おお.
		グラフが軸から離れていく牛ああ.
	内部	グラフが軸から離れていくああ 2回、軸に沿って伸ばしますおお.

多くの場合、関数変換は組み合わせられます。

例えば、関数をプロットする必要があります。これは平方根グラフであり、軸の下に 1 単位移動する必要があります。ああ軸に沿って右に 1 単位おお同時に軸に沿って3回伸ばしますああ.

関数のグラフを構築する直前に、関数の予備的な恒等変換や単純化が必要になる場合があります。

x の x 根が等しいか探しましたか? 。説明と説明を含む詳細な解決策は、最も複雑な問題にも対処するのに役立ちます。x は y のルートであり、例外はありません。宿題、テスト、オリンピック、大学入学の準備をお手伝いします。そして、どのような例を入力しても、どのような数学クエリを入力しても、すでに解決策があります。たとえば、「x は x の根に等しい」とします。

私たちの生活では、さまざまな数学の問題、計算機、方程式、関数が広く使用されています。それらは多くの計算、構造物の建設、さらにはスポーツにも使用されます。人間は古代から数学を使用してきましたが、それ以来、その使用は増加するばかりです。しかし、今では科学は立ち止まっておらず、x の x 根が等しい、y の x 根、x の根、x の根が等しいなどの問題を解決できるオンライン計算機など、その活動の成果を享受できます。 x、x のルートは x に等しい、x のルートは x に等しい、関数 y はマイナス x のルート、関数 y から x のルートを引いたもの、x は y のルート、x は x のルートに等しい。このページには、x の x 根が等しいなど、あらゆる質問を解決するのに役立つ計算機が表示されます。 (たとえば、x の根)。

オンラインで x の根が等しいだけでなく、数学の問題もどこで解決できますか?

x の根が等しいという問題は、私たちの Web サイトで解決できます。無料のオンラインソルバーを使用すると、どんな複雑なオンライン問題でも数秒で解決できます。ソルバーにデータを入力するだけです。また、ビデオ手順を見て、Web サイトでタスクを正しく入力する方法を学ぶこともできます。さらに質問がある場合は、計算機ページの左下にあるチャットで質問することができます。

トピックに関するレッスンとプレゼンテーション: 「平方根関数のグラフ。グラフの定義と構築の領域」

追加資料
ユーザーの皆様、コメント、レビュー、ご要望を忘れずに残してください。すべての資料はウイルス対策プログラムによってチェックされています。

Integral オンラインストアの 8 年生向けの教育補助器具とシミュレーター
Mordkovich A.G.による教科書の電子教科書
8 年生用の電子代数ワークブック

平方根関数のグラフ

みなさん、私たちはすでに関数のグラフの構築に何度も遭遇しました。私たちは多くの線形関数を構築し、放物線。一般に、関数は $y=f(x)$ として記述すると便利です。これは 2 つの変数を含む方程式です。x の各値に対して y が得られます。与えられた操作 f を実行した後、すべての可能な x のセットをセット y にマッピングします。ほぼすべての数学演算を関数 f として書くことができます。

通常、関数をプロットするときは、x と y の値を記録するテーブルを使用します。たとえば、関数 $y=5x^2$ の場合、次の表を使用すると便利です。デカルト座標系上で結果の点をマークし、それらを滑らかな曲線で慎重に接続します。私たちの機能には制限がありません。これらの点を使用する場合のみ、指定された定義領域からの絶対的に任意の値 x、つまり式が意味をなす x を置き換えることができます。

前のレッスンの 1 つで、新しい抽出操作を学習しました。平方根。この操作を使用して、何らかの関数を定義し、そのグラフを構築できるでしょうか?という疑問が生じます。関数 $y=f(x)$ の一般形式を使用してみましょう。 y と x をそのままにして、f の代わりに平方根演算 $y=\sqrt(x)$ を導入します。
数学的演算を知っていたので、関数を定義することができました。

平方根関数のグラフ化

この関数をグラフにしてみましょう。平方根の定義に基づくと、負でない数値、つまり $x≥0$ からのみ平方根を計算できます。
表を作ってみましょう:

座標平面上に点をマークしましょう。

私たちがしなければならないのは、結果として得られた点を慎重に接続することだけです。

皆さん、注目してください。関数のグラフを横にすると、放物線の左枝が得られます。実際、値の表の行を交換すると (上の行と下の行)、放物線だけの値が得られます。

関数 $y=\sqrt(x)$ の定義域

関数のグラフを使用すると、プロパティを簡単に説明できます。
1. 定義範囲: $$。
b) $$。

解決。
この例は 2 つの方法で解決できます。各レターでは、さまざまな方法について説明します。

A) 上で作成した関数のグラフに戻り、セグメントの必要な点をマークしましょう。 $x=9$ の場合、関数が他のすべての値よりも大きいことが明らかにわかります。これは、この時点で最大値に達することを意味します。 $x=4$ の場合、関数の値は他のすべての点よりも小さくなります。これは、これが最小値であることを意味します。

$y_(most)=\sqrt(9)=3$、$y_(most)=\sqrt(4)=2$。

B) 私たちは自分の機能が向上していることを知っています。これは、より大きな引数値がそれぞれより大きな関数値に対応することを意味します。最高値と最低値はセグメントの端で得られます。

$y_(most)=\sqrt(11)$、$y_(most)=\sqrt(2)$。

例2。
方程式を解きます。

$\sqrt(x)=12-x$。

解決。
最も簡単な方法は、関数の 2 つのグラフを作成し、それらの交点を見つけることです。

座標 $(9;3)$ との交点がグラフ上にはっきりと表示されます。これは、$x=9$ が方程式の解であることを意味します。
答え: $x=9$。

この例にはこれ以上の解決策はないと確信できますか? 一方の機能が増加すると、もう一方の機能が減少します。一般に、それらは共通点を持たないか、1 つの点でのみ交差します。

例 3.

関数のグラフを作成して読み取ります。

$\begin (cases) -x, x 9. \end (cases)$

関数の 3 つの部分グラフをそれぞれ独自の間隔で構築する必要があります。

関数のプロパティを説明しましょう。
1. 定義領域: $(-∞;+∞)$。
2. $x=0$ および $x=12$ の場合、$y=0$。 $хϵ(-∞;12)$ の場合 $у>0$; $y 3. 関数は $(-∞;0)U(9;+∞)$ の間隔で減少します。関数は $(0;9)$ の間隔で増加します。
4. 関数は定義領域全体にわたって連続的です。
5. 最大値または最小値はありません。
6. 値の範囲: $(-∞;+∞)$。

自主的に解決すべき問題

1. セグメント上の平方根関数の最大値と最小値を見つけます。
a) $$;
b) $$。
2. 方程式 $\sqrt(x)=30-x$ を解きます。
3. 関数のグラフを作成して読み取ります: $\begin (cases) 2-x, x 4. \end (cases)$
4. 関数 $y=\sqrt(-x)$ のグラフを作成して読み取ります。

トピックに関する記事